(A Û B) = (BÛ A).

Справедливость приведенных законов можно доказать табличным способом: выписать все наборы значений А и В, вычислить на них значения левой и правой частей доказываемого выражения и убедиться, что результирующие столбцы совпадут.

В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений:

ОСНОВНЫЕ ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ

Закон                     Для ИЛИ               Для И

Переместительный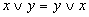                           

Сочетательный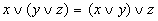                

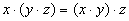
Распределительный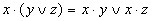          

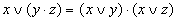
Правила де Моргана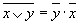                           

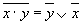
Идемпотенции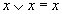                                        

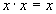
Поглощения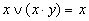                                      

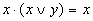
Склеивания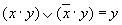                              

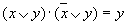
Операция переменной с ее инверсией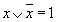                          

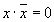
Операция с константами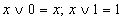            

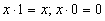
Двойного отрицания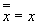   

Практическая часть.

Пример 1. Упростите следующие формулы, используя законы склеивания:

• а)
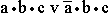
• б)
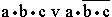
• в)
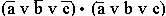
• г)

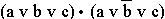
· д)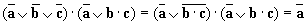
Ответ: а) b•c; б) a; в) c•(a v b) v a•b (Указание: повторить четвертое логическое слагаемое 3 раза); г) a v c.

Пример 2. Упростите следующие формулы, используя законы поглощения:

• а)
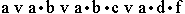
• б)
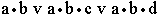
• в)
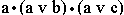
• г)

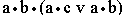
Ответ:  а) a; б) a•b; в) a; г) a•b;

УРОК №9-10

Тема: Составление таблиц истинности.

Цели:

1. Обучающие:
1. Научить доказывать равносильность логических выражений, используя таблицы истинности
2. Закрепить навыки нахождения значений логических выражений посредством построения таблиц истинности
2. Развивающие:
1. Развивать память
2. Развивать речь учащихся
3. Воспитательные:
1. Воспитывать самостоятельность.

Теоретическая часть.

Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.

Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре:

(0, 0), (0, 1), (1, 0), (1, 1).

Если формула содержит три переменные, то возможных наборов значений переменных восемь:

(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).

Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.

Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.

1. Составим таблицу истинности для формулы 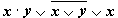, которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу:

Переменные  Промежуточные логические формулы                   Формула

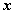
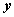
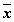
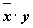
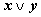
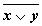
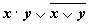
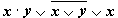
0        0      1     0          0          1          1                     1

0        1      1     1          1          0          1                     1

1        0      0     0          1          0          0                     1

1        1      0     0          1          0          0                     1

Из таблицы видно, что при всех наборах значений переменных x и y формула 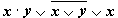принимает значение 1, то есть является тождественно истинной.

Практическая часть.

Пример 1. Постройте таблицы истинности для логических формул и упростите формулы, используя законы алгебры логики:

• а)
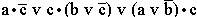
• б)
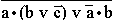
• в)
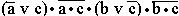
• г)
• д)
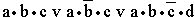
• е)
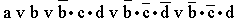
• ж)
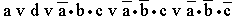
• з)
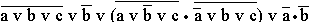
• и)
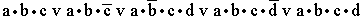
• к)

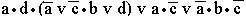
Ответ: а) a v c; б) 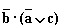; в) ; г) a v c; д) a•(c v b•d); е) ; ж) ; з) 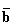; и) a•(b v c•d); к) .

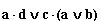УРОК №11-12