В качестве примера рассмотрим высказывание "если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог". Это высказывание формализуется в виде (A v B) → C.
Такая же формула соответствует высказыванию "если Игорь знает английский или японский язык, то он получит место переводчика".
Как показывает анализ формулы (A v B) →C, при определённых сочетаниях значений переменных A, B и C она принимает значение "истина", а при некоторых других сочетаниях — значение "ложь". Такие формулы называются выполнимыми.
Некоторые формулы принимают значение "истина" при любых значениях истинности входящих в них переменных. Таковой будет, например, формула А v ┐А , соответствующая высказыванию "Этот треугольник прямоугольный или косоугольный". Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями.
Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
Если две формулы А и В одновременно принимают одинаковые значения, то они называются равносильными.
Равносильность двух формул алгебры логики обозначается символом "=" или символом "" Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
Практическая часть.
Пример 1. Найдите значения логических выражений:
- а) (lvl) v (lvO);
- б) ((lvO) vl) vl;
- b)(0v1) v (1v0);
- г)(0&1)&1;
- е) ((lvO) & (l&l)) & (Ov l);
- ж) ((l&O) v (l&O)) v l;
- з) ((l&l) v O) & (Ov l);
- и) ((0&0) v0) & (lv l).
Пример 2. Даны два простых высказывания:
А = {2 • 2 = 4}, В = {2 • 2 = 5}.
Какие из составных высказываний истинны:
а) А; б) В;
в) А&В; г)AvB;
д) А=>В; е) А↔В?
Пример 3. Даны простые высказывания:
- А = {Принтер — устройство ввода информации},
- В = {Процессор — устройство обработки информации},
- С = {Монитор — устройство хранения информации},
- D = {Клавиатура — устройство ввода информации}.
Определите истинность составных высказываний:
a) (A&B)&(CvD); б) (А&В)=>(В&С);
в) (AvB) ↔ (C&2>); г) А↔ В.
Пример 4. Дано составное высказывание не (не А и В), где А и В — простые высказывания. В каком случае данное высказывание будет ложным?
Пример 5. Даны простые высказывания:
А = {5>3}, В = {2=3} и С = {4<2}.
Определите истинность составных высказываний
a)(AvB)&C => (A&C)v(B&C);
б) (A&B)vC ↔ (AvC)&(A&B)).
УРОК №5
Тема: Связь между алгеброй логикой и двоичной системой счисления.
Цели:
1.показать применение темы на практике, научиться составлять функции, описывающие состояние электрических схем.
Практическая часть.
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”.
Из этого следует два вывода:
1. одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;
2. на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.
Данные и команды представляются в виде двоичных последовательностей различной структуры и длины. Существуют различные физические способы кодирования двоичной информации.
В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули (или наоборот), например:
УРОК №6
Тема: Логические элементы компьютера.
Теоретическая часть.
Дискретный преобразователь, который после обработки входных двоичных сигналов выдаёт на выходе сигнал, являющийся значением одной из логических операций, называется логическим элементом.
Ниже приведены условные обозначения (схемы) базовых логических элементов, реализующих логическое умножение (конъюнктор), логическое сложение (дизъюнктор) и отрицание (инвертор).
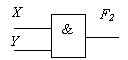
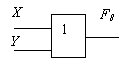
Рис. Конъюнктор, дизъюнктор и инвертор
Устройства компьютера (сумматоры в процессоре, ячейки памяти в оперативной памяти и др.) строятся на основе базовых логических элементов.
Сегодня мы изучим еще один способ представления логических выражений – логические схемы.
Существует три базовых логических элемента, которые реализуют рассмотренные нами три основные логические операции:
· логический элемент «И» — логическое умножение – конъюнктор;
· логический элемент «ИЛИ» — логическое сложение – дизъюнктор;
· логический элемент «НЕ» — инверсию – инвертор.
Поскольку любая логическая операция может быть представлена в виде комбинации трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из “кирпичиков”.
Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс — логический смысл сигнала — 1, нет импульса — 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.
Преобразование сигнала логическим элементом задается таблицей состояний, которая фактически является таблицей истинности, соответствующей логической функции, только представлена в форме логических схем. В такой форме удобно изображать цепочки логических операций и производить их вычисления.
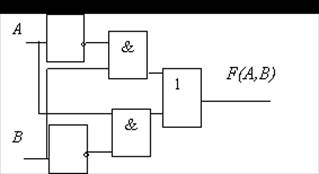
Пример 1. По заданной логической функции F( A, B) = B&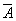 
Ú 
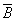&A построить логическую схему.
Построение необходимо начинать с логической операции, которая должна выполняться последней. В данном случае такой операцией является логическое сложение, следовательно, на выходе логической схемы должен быть дизъюнктор. На него сигналы подаются с двух конъюнкторов, на которые, в свою очередь подаются один входной сигнал нормальный и один инвертированный (с инверторов).
Пример 2. Логическая схема имеет два входа X и Y. Определить логические функции F1( X, Y) и F2( X, Y), которые реализуются на ее двух выходах.
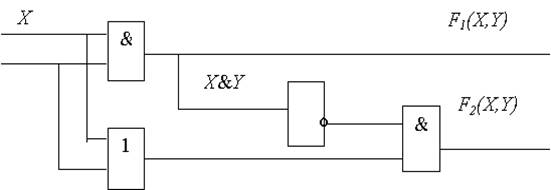
Функция F1( X, Y) реализуется на выходе первого конъюнктора, т.е. F1( X, Y) = X&Y.
Одновременно сигнал с конъюнктора подается на вход инвертора, на выходе которого реализуется сигнал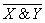 
, который, в свою очередь, подается на один из входов второго конъюнктора.
На другой вход второго конъюнктора подается сигнал XÚY с дизъюнктора, следовательно, функция F2( X, Y) = 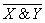& (XÚY).
Рассмотрим схему сложения двух n-разрядных двоичных чисел. При сложении цифр i-го разряда складываются аi и bi, а также pi-1 — перенос из i-1разряда. Результатом будет si – сумма и pi — перенос в старший разряд. Таким образом, одноразрядный двоичный сумматор — это устройство с тремя входами и двумя выходами.
Пример 3. Построить таблицу истинности одноразрядного двоичного сумматора, воспользовавшись таблицей сложения двоичных чисел.
Входы Выходы
Ai Bi Pi-1 Si Pi
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1
УРОК №7
Дата: 2018-12-21, просмотров: 296.
