Теоретическая часть.
Логическая операция ИМПЛИКАЦИЯ (логическое следование):
в естественном языке соответствует обороту если ..., то ...;
обозначение →.
Импликация - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.
А В А→В
0 0 1
0 1 1
1 0 0
1 1 1
Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность):
в естественном языке соответствует оборотам речи тогда и только тогда; в том и только в том случае;
обозначения ~.
Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. Таблица истинности эквиваленции:
А В А ~ В
0 0 1
0 1 0
1 0 0
1 1 1
Практическая часть.
Пример 1. Формализуйте предостережение, которое одна жительница древних Афин сделала своему сыну, собиравшемуся заняться политической деятельностью: “Если ты будешь говорить правду, то тебя возненавидят люди. Если ты будешь лгать, то тебя возненавидят боги. Но ты должен говорить правду или лгать. Значит, тебя возненавидят люди или возненавидят боги”.
Формализуйте также ответ сына: “Если я буду говорить правду, то боги будут любить меня. Если я буду лгать, то люди будут любить меня. Но я должен говорить правду или лгать. Значит, меня будут любить боги или меня будут любить люди”.
Ответ: Решение. Введем обозначения для логических высказываний: а – “ты будешь говорить правду”; b – “тебя возненавидят люди”; c – “тебя возненавидят боги”. Договоримся считать, что некоторое заданное высказывание x истинно, если нет оговорки. Тогда предостережение матери можно записать так:
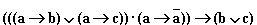. А ответ сына – так:
.
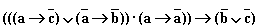Пример 2. Пусть a = “это утро ясное”, а b = “это утро теплое”. Выразите следующие формулы на обычном языке:
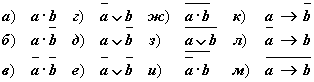
Ответ:
а) “это утро ясное и тёплое”; ж) “это утро не ясное или не тёплое”;
б) “это утро ясное и оно не тёплое”; з) “это утро не ясное и не тёплое”;
в) “это утро не ясное и оно не тёплое”; и) “это утро ясное или не тёплое”;
г) “это утро не ясное или оно тёплое”; к) “если это тро ясное, то оно не тёплое”;
д) “это утро ясное или оно не тёплое”; л) “если это утро не ясное, то оно тёплое”;
е) “это утро не ясное или оно не тёплое”; м) “это утро ясное и не тёплое”.
Пример 3. Из двух данных высказываний a и b постройте составное высказывание, которое было бы:
- а) истинно тогда и только тогда, когда оба данных выказывания ложны;
- б) ложно тогда и только тогда, когда оба данных высказывания истинны.
Ответ : а)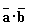 
; б) 
.
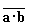Пример 4. Из трех данных высказываний a, b, c постройте составное высказывание, которое истинно, когда истинно какое-либо одно из данных высказываний, и только в этом случае.
Ответ: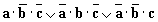 
.
УРОК №4
ТЕМА: ЛОГИЧЕСКИЕ ФОРМУЛЫ
Теоретическая часть.
Запишем в форме логического выражения составное высказывание
(2*2=5 или 2*2=4) и (2*2 ≠ 5 или 2*2 ≠ 4)
Проанализируем составное высказывание. Что оно содержит?
Оно содержит два простых высказывания:
А= ”2*2=5” – ложно (0)
В= “2*2=4” – истинно (1)
Тогда давайте перепишем составное высказывание. Что получится?
(А или В) и (А или В)
Теперь необходимо записать высказывание в форме логического выражения.
Что нужно сделать для этого? Нужно подставить знаки логических операций
(AvB)&(AvB)
Теперь выполняем логические операции, причем в строго определенном порядке:
- отрицание,
- конъюнкция,
- дизъюнкция,
- импликация,
- эквиваленция
Подставим в логическое выражение значения логических переменных и получим значение логической функции:
F = (AvB)&(AvB) = (0v1) & (1v0) = 1&1 = 1
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.
Определение логической формулы:
Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0") — формулы.
Если А и В — формулы, то ┐А, А . В , А v В , А B , А В — формулы.
Дата: 2018-12-21, просмотров: 330.
