Цели:

1. Обучающие:
1. познакомить с законами алгебры логики и научить их применять на практике
2. Закрепить навыки нахождения значений логических выражений посредством построения таблиц истинности и используя законы алгебры логики
2. Развивающие:
1. Развивать логическое мышление
3. Воспитательные:
1. Воспитывать аккуратность ведения тетради

Теоретическая часть.

Логические выражения называются равносильными, если их истинностные значения совпадают при любых значениях, входящих в них логических переменных.

В алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений. Приведем соотношения, отражающие эти законы.

Закон двойного отрицания:

 А = 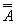. Двойное отрицание исключает отрицание.

Переместительный (коммутативный) закон:

А v B = B v A; — для логического сложения:

A&B = B&A. — для логического умножения:

Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.

В обычной алгебре a + b = b + a, a v b = b v a.

Сочетательный (ассоциативный) закон:

 (A v B) v C = A v (B v C) — для логического сложения:

 (A&B)&C = A&(B&C)— для логического умножения:

При одинаковых знаках скобки можно ставить произвольно или вообще опускать.

В обычной алгебре:

(a + b) + c = a + (b + c) = a + b + c,

Распределительный (дистрибутивный) закон:

 (A v B)&C = (A&C) v (B&C); — для логического сложения

 (A&B) v C = (A v C)&(B v C). — для логического умножения:

Определяет правило выноса общего высказывания за скобку.

В обычной алгебре:

(a + b) * c = a * c + b * c.

5. Закон общей инверсии (законы де Моргана):

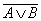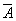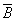 = & ; — для логического сложения

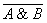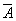 = v 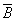— для логического умножения:

6. Закон идемпотентности

( от латинских слов idem — тот же самый и potens —сильный; дословно — равносильный):

A v A = A; — для логического сложения:

A&A = A. — для логического умножения

Закон означает отсутствие показателей степени.

Законы исключения констант:

A v 1 = 1, A v 0 = A; — для логического сложения:

A&1 = A, A&0 = 0. — для логического умножения:

Закон противоречия:

A& 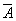= 0.

Невозможно, чтобы противоречащие высказывания были одновременно истинными.

Закон исключения третьего:

A v 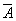= 1.

Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.

Закон поглощения:

A v (A&B) = A; — для логического сложения:

A&(A v B) = A. — для логического умножения

Закон исключения (склеивания):

 (A&B) v ( 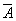&B) = B; — для логического сложения:

 (A v B)&( 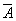 v B) = B. — для логического умножения: