1. Определить по табл. 1 для условий опыта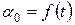 
.
2. Вычислить и записать в таблицу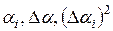 
.
3. Вычислить доверительный интервал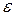 
по заданной доверительной вероятности 
.
.
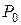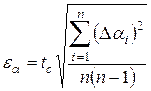4. Оценить границу абсолютной допустимой ошибки манометра.
5. Вычислить относительную приборную ошибку, допущенную при определении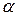 
.
,
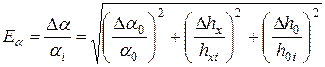где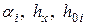 
берутся из таблицы и соответствуют случаю, когда 
, 
.
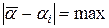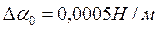6. Вычислить абсолютную приборную погрешность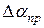 
:
.
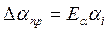7. Сравните абсолютную приборную погрешность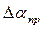 
и доверительный интервал 
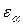. Если они одного порядка, то ошибка измерения 
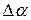вычисляется по формуле:
.
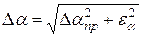Если они отличаются хотя бы на порядок, то берётся наибольшая ошибка.
8. Окончательный результат запишите в виде:
.
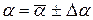Контрольные вопросы
1. Приведите примеры, подтверждающие существование поверхностного натяжения жидкостей. Как можно уменьшить поверхностное натяжение?
2. Дайте (сформулируйте) определение коэффициента поверхностного натяжения. В каких единицах он измеряется в системе СИ?
3. Объясните, почему горячая мыльная вода лучше моет посуду и бельё, чем холодная чистая вода или холодная мыльная вода.
4. Объясните, почему вода поднимается в стеклянных капиллярах, а ртуть в тех же капиллярах опускается по отношению к свободной поверхности жидкости.
5. Чему равен коэффициент поверхностного натяжения жидкости (например, воды) при критической температуре?
6. Объясните сущность метода Ребиндера и укажите порядок выполнения данной лабораторной работы.
7. Укажите основные причины ошибок определения коэффициента поверхностного натяжения жидкости применяемым методом.
ЛАБОРАТОРНАЯ РАБОТА №7
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЁМКОСТЕЙ ГАЗА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ И ПОСТОЯННОМ ОБЪЁМЕ МЕТОДОМ АДИАБАТИЧЕСКОГО РАСШИРЕНИЯ
1. Цель работы: Изучение изопроцессов, закономерностей адиабатического процесса и экспериментальное определение показателя адиабаты для воздуха при комнатной температуре.
Краткая теория.
Основные закономерности адиабатического процесса изучаются на примере поведения идеального газа.
Идеальный газ — это некий абстрактный газ, удовлетворяющий следующим условиям: 1) соударения молекул такого газа происходят как соударения упругих шаров; 2) размеры молекул пренебрежимо малы; 3) между молекулами отсутствуют силы взаимного притяжения и отталкивания.
Всякий реальный газ по мере убывания его плотности приближается по свойствам к идеальному. Обычный воздух при комнатной температуре и атмосферном давлении можно приближённо считать идеальным газом. Состояние некоторой массы газа определяется значениями трёх параметров: давления 
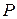, объема 
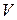и температуры 
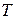. В том случае, когда из этих трёх параметров при изменении состояния газа один остаётся постоянным, процесс перехода называется изопроцессом.
Для идеального газа строго выполняются законы Бойля-Мариотта,
Гей-Люссака и Шарля. Эти законы описывают состояния газа для случаев, когда один из параметров остаётся постоянным.
Закон Бойля-Мариотта описывает изотермический процесс, т. е. процесс, протекающий при постоянной температуре (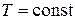 
): для данной массы газа при постоянной температуре произведение давления газа на объём есть величина постоянная
.
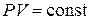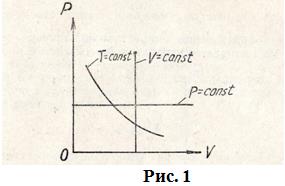
Графически это соотношение изображается гиперболой (рис. 1). Каждому значению температуры соответствует своя кривая. Эти кривые называются изотермами.
Закон Гей-Люссака описывает изобарический процесс, т. е. процесс, протекающий при постоянном давлении (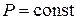 
): отношение объёма данной массы газа к температуре, при которой он находится, есть величина постоянная:
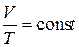. (2)
Закон Шарля описывает изохорический процесс, т. е. процесс, протекающий при постоянном объёме (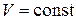 
): отношение давления газа к температуре, при которой он находится, есть величина постоянная:
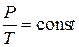. (3)
Графически соотношения (2) и (3) изображены в координатах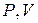 
на рис. 1.
Первое начало термодинамики выражает закон сохранения энергии и формулируется следующим образом: количество тепла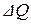 
сообщённое системе, идёт на приращение внутренней энергии 
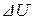системы и на совершение системой работы 
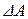против внешних сил:
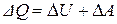. (4)
Для бесконечно малого изменения состояния системы уравнение (4) примет вид:
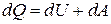. (5)
Адиабатическим процессом называется процесс, протекающий без теплообмена с внешней средой. Близкими к адиабатическому могут быть быстро протекающие процессы, так как количество тепла, которым обменивается система с внешней средой, будет тем меньше, чем меньшее время длится процесс.
Для адиабатического процесса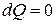 
, тогда из (5) следует:
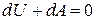
или
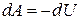, (6)
т. е. работа в адиабатическом процессе совершается за счёт убыли внутренней энергии.
Для идеального газа при адиабатическом процессе функциональная связь между давлением и объёмом определяется уравнением Пуассона:
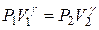, (7)
где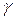 
— показатель степени, численно равный отношению молярных теплоёмкостей данного газа, т. е.:
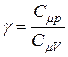. (8)
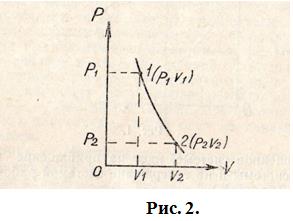
Кривая, изображающая адиабатический процесс в координатах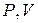 
называется адиабатой (рис. 2).
Теплоёмкость газа — это физическая величина, численно равная количеству тепла, которое необходимо сообщить системе для нагревания её на один Кельвин (градус):
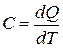. (9)
В системе СИ теплоёмкость имеет размерность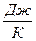 
.
Различают удельную и молярную теплоёмкости.
Теплоёмкость единицы массы вещества называют удельной теплоёмкостью:
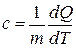. (10)
Она обозначается буквой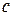 
и имеет и имеет размерность 
.
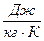Теплоёмкость одного моля вещества называется молярной:
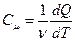, (11)
где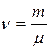 
— число молей вещества; 
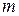— масса вещества; 
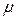— молярная масса. Молярная теплоёмкость имеет размерность 
.
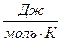Теплоёмкость моля вещества и удельная теплоёмкость связаны очевидным соотношением:
.
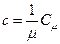Величина теплоёмкости газов существенно зависит от условий, при которых протекает процесс: при постоянном объёме или при постоянном давлении.
Если нагревание газа происходит при постоянном объёме, то газ не совершает работы против внешних сил, так как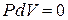 
. Из уравнения первого начала термодинамики следует:
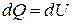, (12)
т. е. при изохорическом процессе всё тепло, сообщенное газу, идёт на приращение его внутренней энергии. Напомним, что внутренняя энергия идеального газа является функцией только температуры. Следовательно, для одного моля идеального газа имеем:
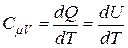. (13)
Внутренняя энергия одного моля идеального газа определяется уравнением:
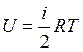, (14)
где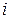 
— число степеней свободы молекулы данного газа (число независимых координат, которые полностью определяют положение молекулы в пространстве, называется числом степеней свободы молекулы); 
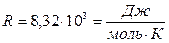- универсальная газовая постоянная.
Для бесконечно малого изменения температуры из уравнения (14) следует:
,
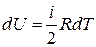откуда
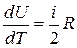. (15)
С учётом (15) выражение (13) приводится к виду
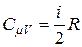. (16)
Если нагревание газа происходит при постоянном давлении, то согласно первому началу термодинамики тепло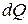 
, сообщённое газу, затрачивается не только на увеличение его внутренней энергии 
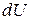, но и на совершение газом работы 
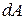, то есть:
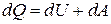. (17)
Для изобарического процесса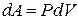 
, поэтому (17) можно записать в виде:
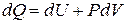
Теплоёмкость моля газа при постоянном давлении равна:
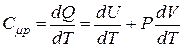. (18)
Первое слагаемое правой части этого равенства равно молярной теплоёмкости газа при постоянном объёме. Запишем уравнение состояния идеального газа для случая бесконечно малого изменения его параметров:
,
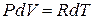откуда
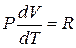. (19)
Таким образом, второе слагаемое равенства (18) численно равно универсальной газовой постоянной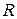 
.
Выражение молярной теплоёмкости газа при постоянном давлении с учётом (15) и (19) приводится к виду:
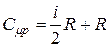, (20)
а так как
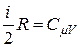, (21)
то
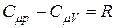. (22)
Это выражение называется уравнением
Майера.
Анализ формул (16) и (20) приводит к выводу, что для идеального газа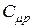 
и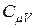 
не зависят от параметров состояния газа 
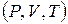, а определяются только числом степеней свободы молекул. Для реальных газов этот вывод удовлетворительно согласуется с опытом при невысоких температурах. При более высоких температурах становится существенной зависимость теплоёмкости и, следовательно, показателя адиабатического процесса 
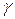от температуры, что необходимо учитывать при расчётах.
Разделив почленно (20) на (16), имеем:
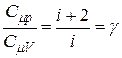. (23)
Так как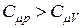 
, то показатель адиабаты 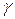всегда больше единицы.
Поэтому адиабата круче спадает к оси абсцисс, чем изотерма (рис. 3).
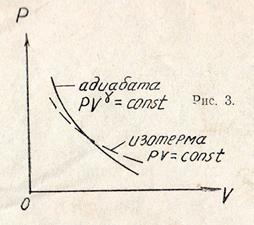Соотношение (23) позволяет вычислить величину 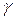для любого газа, если известно число степеней свободы молекул этого газа. Например, для одноатомных газов 
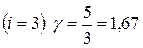; для двухатомных газов 
.
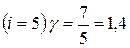Этот результат можно проверить на опыте, что и является целью настоящей работы.
Дата: 2018-12-21, просмотров: 395.
