Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Во время домашней подготовки к лабораторной работе №4, в целях экономии времени на занятии, рекомендуется в пункте 4 «Анализ и обработка результатов измерений» построить теоретический график зависимости периода колебаний от длины нити. При этом длину нити можно взять, например, 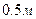, , 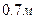, 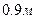а период колебаний вычислить по формуле (18). При выполнении работы нанести на этот же график точки экспериментальной зависимости и объяснить расхождение результатов.

При подготовке к лабораторной работе №5 необходимо ознакомится с п.3 лабораторной работы №1 (часть I), а именно, правилами измерения микрометром.

При подготовке к лабораторной работе №6 рекомендуется в п.1 «Краткая теория» привести таблицу коэффициента поверхностного натяжения жидкостей, взяв её, например, из [3]. При выполнении работы, перед тем как снимать показания с - образного манометра, необходимо сначала научиться открывать кран аспиратора плавно, чтобы из стеклянного капилляра выходило как можно меньшее количество пузырьков.

При выполнении лабораторной работы №7 необходимо кран 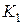 открывать и закрывать быстро (кран должен быть открытым около 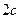). Кран  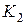закрывать быстро, сразу же после остановки насоса.

 

 

ЛАБОРАТОРНАЯ РАБОТА№4

ИЗУЧЕНИЕ ЗАКОНОВ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ

1. Цель работы: Изучение основных законов колебательного движения на примере математического и физического ма­ятников.

Краткая теория

Колебания представляют один из наиболее распространённых видов движений и весьма разнообразны по своей физической природе. Маятник часов, звук, свет, переменный электрический ток являются примерами колебаний тех или иных физических величин. Однако при всём разнообразии колебаний (механических или электромагнитных) закономерности колебательных процессов имеют между собой много общего.

Напомним, что колебательным движением твёрдого тела (системы) называется движение, характеризующееся той или иной степенью повторяемости во времени. Колебания, при которых движение тела повторяется через равные промежутки времени, называются периодическими колебаниями. Для характеристики периодического колебательного движения используются такие величины, как смещение ( 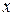), амплитуда ( 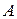), период ( 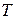) и частота ( ).

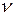Смещением называется величина, характеризующая положение тела в данный момент времени относительно его положения равновесия.

Наибольшее отклонение тела от положения равновесия называется амплитудой колебаний.

Наименьший промежуток времени, по истечении которого движение тела (системы) повторяется, называется периодом колебаний. Величина обратная периоду колебаний, называется частотой колебаний. Она определяет число полных колебаний за единицу времени, т. е.

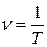.                                  (1)

За единицу частоты в СИ принимается частота такого колебания, период которого равен 1 секунде. Эту единицу называют герцем (Гц).

Важной характеристикой колебательного движения является так называемая круговая (циклическая) частота:

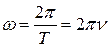,                                      (2)

которая определяет число колебаний тела за 2π секунд.

Простейшим случаем периодического колебательного движения являются гармонические колебания, при которых изучаемая физическая величина изменяется по закону синуса или косинуса.

Гармонические колебания совершает, например, тело, на которое действует только упругая или квазиупругая сила.

Квазиупругой силой называется сила, которая не является по своей природе упругой, но пропорциональна 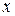, то есть она удовлетворяет тому же условию, как и упругая сила

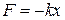,                                               (3)

где 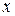 — смещение тела от положения равновесия.

Если гармонические колебания происходят только под действием упругой или квазиупругой силы, то частота колебаний не зависит от начальных условий и определяется только свойствами самой колеблющейся системы. На этом основании эта частота называется собственной частотой и обозначается 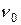 или 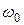, а сами колебания называются собственными или свободными колебаниями.

Гармонические колебания тела описываются линейным однородным дифференциальным уравнением второго порядка

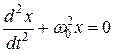.                                     (4)

Решение этого уравнения может быть записано в следующем виде:

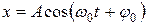,                              (5)

или

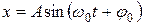,                               (6)

где 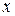 — смещение (отклонение) колеблющейся системы от положения равновесия;  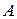— амплитуда колебания.

Аргумент 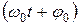 стоящий под знаком косинуса (синуса), носит название фазы колебания. Величина  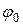называется начальной фазой.

Начальная фаза характеризует колебательный процесс в начальный момент времени, т. е. при 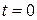. Фаза, как физическая величина, сама является функцией времени. В случае гармонических колебаний фаза определяется, как уже отмечалось выше, равенством:

.

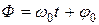Легко убедиться в том, что первая и вторая производные от гармонически колеблющейся величины 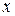 также изменяются по гармоническому закону. Так, например, дифференцируя (6) имеем:

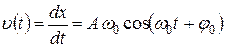,                        (7)

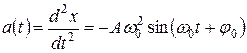.                    (8)

Из (7) и (8) следует, что при гармонических колебаниях скорость и ускорение тела, также как и его смещение, изменяются по периодическому (гармоническому) закону. При этом скорость 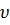 опережает смещение по фазе на 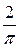, а ускорение ( 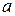) и смещение ( 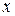) находятся в противофазе. Это хорошо видно на рис. 1, где показаны графики изменения во времени смещения 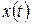, скорости  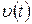и ускорения  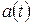для одной и той же механической колебательной системы.

     

При изучении законов колебательного движения механических систем в лабораторных условиях, как правило, используют колебательные системы, имеющие одну степень свободы. К числу таких систем относятся математический маятник на бифилярном подвесе и физический маятник.

Физическим маятником называется тело, укреплённое на неподвижной горизонтальной оси, не проходящей через его центр масс, и способное совершать колебания относительно этой оси.

При отклонении маятника от положения равновесия на некоторый угол 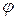 возникает вращающий момент, стремящийся вернуть маятник в положение равновесия.

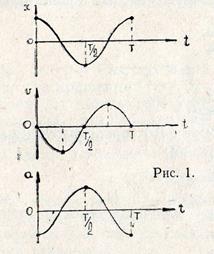
Величина этого момента, как это следует из рис. 2, равна:

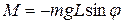                                    (9)

где 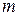 — масса маятника;  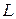— расстояние между точкой подвеса и центром масс маятника. Знак «–» в формуле (9) объясняется тем, что векторы  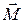и 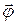 направлены в противоположные стороны.

В случае малых отклонений от положения равновесия физический маятник совершает гармонические колебания. Докажем это.

Пусть точка 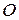 является центром масс физического маятника. В процессе колебаний центр масс тела совершает движение по дуге окружности радиуса 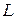. Обозначим момент инерции маятника относительно оси вращения, проходящей через точку 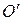, символом 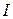. Согласно основному закону динамики вращательного движения

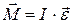,                                             (10)

где

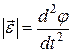.                                             (11)

Приравнивая правые части (9) и (10), пренебрегая трением и учитывая выражение (11), получаем:

.

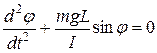При малых углах отклонения маятника можно принять 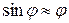, тогда:

,

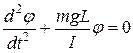а вводя обозначение

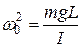,                                           (12)

получим уравнение, аналогичное (4):

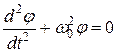.                                    (13)

Решение этого дифференциального уравнения аналогично (5) и записывается в виде:

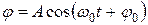.                                       (14)

Из (14) следует, что 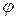 является периодической функцией и изменяется по закону косинуса. Правильность этого решения можно проверить, дифференцируя (14) два раза по времени.

Следовательно, можно считать, что физический маятник, отклонённый на малый угол, (когда выполняется условие 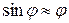), будет совершать гармонические колебания. Период колебания физического маятника определяется выражением:

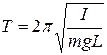,                                      (15)

что следует из формулы (2) с учётом (12).

В (15) символом 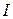 обозначен момент инерции физического маятника относительно оси, проходящей через точку  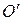рис. 2.

Напомним, что момент инерции твёрдого тела относительно заданной оси равен сумме моментов инерции отдельных составляющих его частиц (материальных точек):

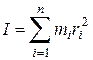,                                         (16)

где 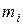и 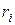 — соответственно масса i-й частицы и её расстояние до оси вращения (i = l, 2,…, п).

Если для какого-либо тела известен его момент инерции 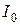 относительно оси, проходящей через центр масс, то момент инерции относительно любой оси, параллельной первой, может быть найден по теореме Штейнера:

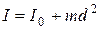,                                        (17)

где 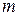 — масса тела,  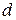— расстояние между осями.

В данной лабораторной работе формулы (15) и (17) используются для определения момента инерции физического маятника (задание № 1).

Математическим маятником называется колебательная система, состоящая из материальной точки, «прикреплённой» к концу гибкой, нерастяжимой и невесомой нити, второй конец которой закреплён неподвижно. Близким к математическому, является маятник, представляющий собой тяжёлый шарик, подвешенный на тонкой нерастяжимой нити (рис. 3).

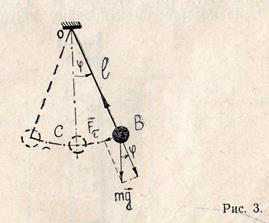Отклонение маятника от положения равновесия будем характеризовать углом 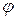, образованным с нитью вертикально.

При отклонении маятника от положения равновесия возникает вращающий момент, модуль которого равен 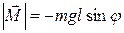, где 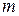 — масса, а  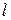— длина маятника.

При малых углах 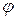 (когда можно принять 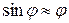) свободные колебания математического маятника можно считать гармоническими с периодом:

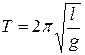                                             (18)

где 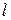 — длина маятника,  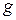— ускорение силы тяжести.

Малые колебания математического маятника (когда 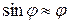) являются также гармоническими (аналогично физическому маятнику). Формула (18) получается, если в (15) подставить значение момента инерции математического маятника относительно точки подвеса: .

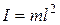Как следует из формулы (18), период колебаний математического маятника зависит (при отсутствии трения) только от его длины 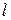 и ускорения силы тяжести 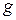. Экспериментальная проверка указанной зависимости и составляет содержание задания № 2 данной лабораторной работы.

 

Описание установки

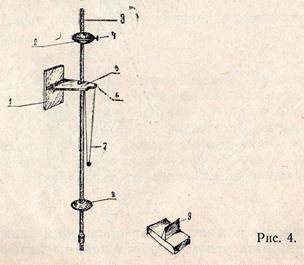В данной лабораторной работе законы колебательного движения будем изучать с помощью универсального маятника (прибор ФП1А).

Прибор ФП1А (рис. 4) включает в себя настенный кронштейн 1, на котором смонтирована подушка опорных призм 5 и узел 6 крепления нитей бифилярного подвеса математического маятника 7. На кронштейне 1 подвешен (на опорной призме 5) физический маятник, представляющий собой металлический стержень 3, на котором закреплены два тяжелых груза — чечевицы 2 и 8. Таким образом, универсальный маятник (прибор ФП1А) сочетает в себе два типа маятников: физический и математи­ческий. Конструкция прибора обеспечивает вращение обоих маятников около одной и той же оси, проходящей через опорную плоскость подушек 5.

В комплект прибора входит специальная подставка 9 с призмой для нахождения центра масс маятника.

 

Порядок выполнения работы

Задание 1. Определение момента инерции физического маятника.

Приборы и принадлежности : физический маятник (прибор ФП1А), секундомер, металлическая линейка с ценой деления 1 мм, подставка с призмой для нахождения центра тяжести маятника.

При выполнении задания № 1 рекомендуется соблюдать указанную ниже последовательность выполнения работы.

1. Вывести и записать, используя выражение (15), расчётную формулу для определения момента инерции физического маятника.

2. Приготовить таблицу для записи исходных данных и результатов опыта (табл. 1).

Номер опыта	m, кг	∆ m, кг	L, м	∆ L, м	N	τ, с	Т, с	∆Т, с	I, кг·м2	∆ I, кг·м2
1 . . . n

 

3. Зафиксировать грузы (чечевицы) на стержне физического маятника по указанию преподавателя.

Определить и записать в табл. 1 массу т физического маят­ника (масса обычно указана на маятнике или сообщается преподавателем).

4. Положить маятник на ребро трёхгранной призмы (рис.5) и, добившись положения устойчивого равновесия маятника, измерить длину L от точки подвеса до центра масс этого маятни­ка. Указанные измерения величины L выполнить не менее 5-ти раз. Результаты всех измерений записать в табл. 1.

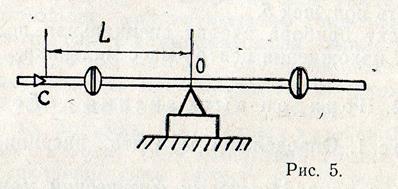5. Повесить маятник на кронштейн 1 (рис. 4). Отклонить маятник на угол 5—10° и предоставить ему возможность совершать малые колебания.

6. Измерить с помощью секундомера время 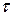 20-ти полных колебаний. Измерения  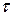повторить не менее 5-ти раз. Число полных колебаний N может быть и другим (N = 30, N=40 и т. д.). Результаты всех измерений записать в табл. 1.