1. Цель работы: Изучение основных законов движения вязкой жидкости, определение коэффициента внутреннего трения методом Стокса.

Краткая теория

Внутреннее трение (вязкость) жидкостей относится к разделу физики, называемому физической кинетикой, предметом изучения которой являются необратимые процессы. Свойства каждого кинетического процесса определяются как внешними условиями, в которых находится вещество, так и внутренними свойствами вещества. Изучение кинетических процессов является источником ценной информации о силах взаимодействия между частицами вещества.

Каждый кинетический процесс приводит хотя бы к одному из явлений переноса, которые называются диффузией, теплопроводностью, вязкостью, электропроводностью.

Диффузия (перенос вещества), теплопроводность (перенос энергии в форме тепла), вязкость (перенос импульса) являются необратимыми процессами, возникающими самопроизвольно вследствие теплового движения при отклонении вещества от равновесного состояния. Это отклонение выражается соответственно в неоднородном распределении вещества, его температуры, в различии скоростей движения макроскопических частиц среды.

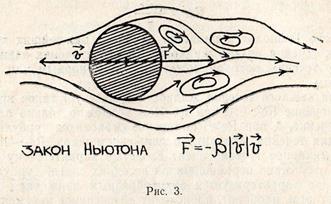
Механизм вязкости заключается в молекулярном перемешивании, обусловленном тепловым движением. Вязкость проявляется в появлении силы сопротивления относительному движению слоёв жидкости или газа. Основным феноменологическим законом, описывающим явление вязкости, является закон Ньютона:

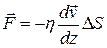,                               (1)

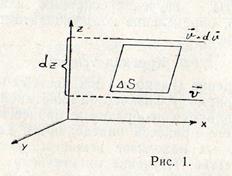
где  — сила внутреннего трения соприкасающихся слоёв жидкости (газа); — коэффициент внутреннего трения или динамической вязкости; 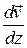 - градиент скорости упорядоченного движения, характеризующий изменение скорости потока вдоль оси  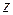(см. рис. 1);  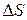— величина площади соприкасающихся слоев;  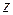— направление, перпендикулярное скорости движения слоёв жидкости (газа).

Единицей вязкости в СИ является такая вязкость, при которой градиент скорости, равный 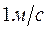 на 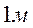, приводит к возникновению силы внутреннего трения в  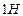на 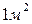. Таким образом, коэффициент динамической вязкости имеет размерность

.

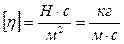Широко применяется и единица измерения вязкости системы СГС, названная пуазом (Пз) в честь французского учёного Ж. Пуазейля, впервые в середине прошлого столетия исследовавшегося течения вязкой жидкости:

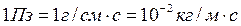.                              (2)

Свойства течения вязкой жидкости зависят от её плотности , динамической вязкости , а также от характерных для данного течения скорости 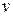 и линейного размера 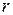. Например, для течения, вызванного движением шара, характерным размером является радиус шара, а характерная скорость — скорость движения шара. Для течения жидкости по трубе характерным линейным размером является диаметр трубы, а характерной скоростью — средняя скорость потока.

Легко показать, что из величин 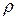, , 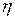 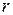и 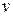 можно образовать лишь одну безразмерную комбинацию, названную числом Рейнольдса и обозначаемую через Re:

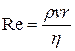.                                    (3)

Число Рейнольдса является одной из важнейших характеристик течения вязкой жидкости, от его значения зависит характер течения, которое может быть ламинарным или турбулентным.

Для каждого течения жидкости существует такое критическое значение 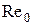, что при  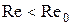возможно только ламинарное течение, а при  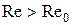течение становится турбулентным. Так, для течения, вызванного движением шара .

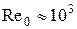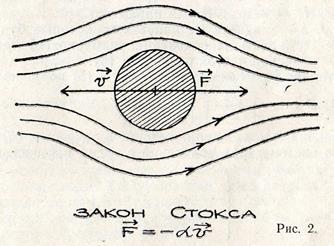Ламинарное течение носит слоистый характер, ему свойственно отсутствие перемешивания соседних слоёв. Турбулентное движение характеризуется вихреобразным движением среды, при котором, наоборот, происходит интенсивное перемешивание вещества в макроскопических масштабах. Эти два режима течения характеризуются различными зависимостями силы соп­ротивления от скорости (см. рис. 2, 3).

Установим, с какой силой вязкая среда действует на движущееся в ней тело. Рассмотрим вначале ламинарное течение, которое имеет место при малых скоростях течения. Критерием малости является условие:

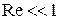.              (4)

В этом случае сила сопротивления обусловлена переносом импульса и зависит от динамической вязкости 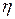, скорости течения  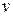и характерного размера 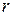. Установим зависимость силы сопротивления от физических параметров методом анализа размерностей. Предполагая, что искомая функциональная зависимость является степенной, можем записать:

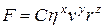,                               (5)

где 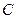 — безразмерный параметр;  — неизвестные константы, которые будут определены из сравнения размерностей правой и левой частей равенства (5).

Подставляя размерность 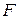, , 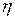 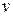и 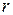 в (5) получаем:

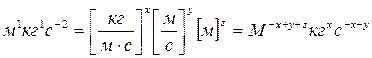.              (6)

Приравнивая показатели степеней в равенстве (6), получаем линейную систему трёх уравнений с тремя неизвестными:

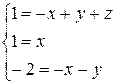
Единственным решением этой системы является 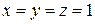, что позволяет однозначно установить функциональную зависи­мость (5):

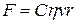,                                    (7)

где безразмерный коэффициент 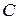 зависит от формы тела и методом анализа размерностей, естественно, определён быть не может. Английский ученый Дж. Стокс показал, что для шара

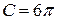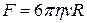 и ,                                    (8)

где 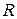 — радиус шара.

При турбулентном движении (большие 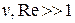) перемешивание жидкости становится макроскопическим и определяющей становится не вязкость жидкости, а её плотность 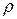. Методом анализа размерностей легко показать, что в этом случае

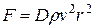,                                         (9)

где 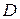 — безразмерный коэффициент, сильно зависящий от формы тела. В общем случае закон действия силы сопротивления имеет вид:

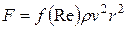,                                  (10)

где безразмерная функция 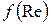 определяется экспериментально.

Анализ размерностей является одним из универсальных методов исследования физических явлений и очень прост в применении.
(Великий физик Энрико Ферми часто повторял, что действительно понимающие природу того или иного явления должны получать основные соотношения из соображений раз­мерности).

Динамическая вязкость газов растёт с увеличением температуры по закону, близкому к 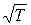. Незначительные отклонения от этого закона обусловлены небольшим изменением эффективного сечения молекул  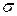с температурой.

Динамическая вязкость жидкостей с увеличением температуры сильно уменьшается в соответствии с законом, открытым советским физиком Я. И. Френкелем (закон Френкеля-Андраде):

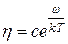,                                              (11)

где 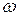 — энергия активации молекулы;  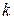— постоянная Больцмана, а множитель  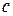зависит от химического состава жидкости и слабо — от температуры. Например, вязкость воды при изменении температуры от 0°С до 100°С уменьшается от  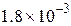до .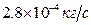

Динамическая вязкость некоторых жидкостей при различных температурах приведена в табл. 1.

Таблица 1

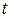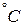
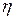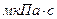
Жидкость	,	,	Жидкость	,	,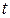
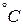
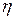Вода	0	1788	Масло касто­ровое	10	242·104
	20	1004	Масло подсолнечное	20 100	50000 2770
Глицерин	-20	134·106
	0	121·105	Мёд	20	650·104
	20	1499·103		80	100·103
	100	12945
	200	216	Молоко цельное	5 20	2960 1790
Молоко сгущенное	20	1245·103		80	570
(с сахаром)
			Рыбий жир	20	45600
Раствор спирта этилового в воде (20%-ный)	20	1960	Сливки (жирностью 40%)	80 20	4600 6900

Теория метода Стокса

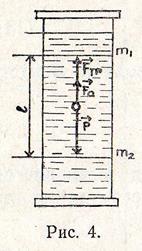
Одним из способов определения коэффициента вязкости является метод Стокса, основанный на использовании закона Стокса (8) и измерении времени (скорости) движения в исследуемой жидкости тяжёлого металлического шарика малого радиуса.

Если небольшой шарик падает вертикально в вязкой жидкости, то он испытывает действие трёх коллинеарных сил (см. рис. 4): силы тяжести 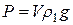, выталкивающей силы Архимеда  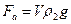и силы сопротивления (трения):

,

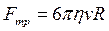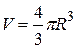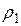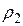где  — объём шарика;  и   – плотности материала шарика и исследуемой жидкости соответственно.

На основании второго закона Ньютона имеем:

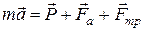,                               (12)

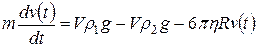.                  (12΄)

Решением этого уравнения, удовлетворяющим начальному условию 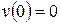, является:

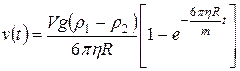.                               (13)

Через небольшой промежуток времени 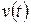 становится почти постоянной (скорость установившегося движения) и равной

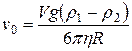.                           (14)

Решая это уравнение относительно 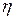 и переходя к диаметру шарика 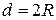, получаем:

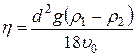 .                              (15)

Скорость установившегося движения вычисляется по экспериментально измеряемому времени 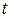  его движения (падения) на участие длины :

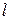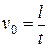.                      (16)

Окончательно расчётная формула для определения коэффициента вязкости 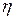 примет вид:

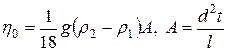,     (17)

где 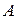 содержит все экспериментально измеряемые физические величины.

Формулы (15) и (17) справедливы для шарика, движущегося в бесконечно простирающейся жидкости. Для учёта влияния стенок и дна цилиндра, а также верхней поверхности жидкости на движение шарика необходимо в формулу (17) ввести безразмерный поправочный множитель:

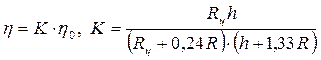                   (18)

4. Описание установки

Приборы для измерения вязкости жидкости называются вискозиметрами. В данной работе применяется прибор, представляющий собой высокий стеклянный цилиндр, установленный вертикально (рис. 4), в который налита исследуемая жидкость. Сосуд накрыт крышкой с отверстием, через которое при опытах опускаются металлические шарики небольшого диаметра. На цилиндре имеются две метк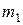и и 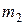, расположенные на расстоянии  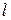друг от друга.

Уровень жидкости в сосуде должен быть выше верхней метки на 8-10 см. Это необходимо для того, чтобы к моменту подхода шарика к верхней метке движение шарика уже было бы установившимся, т. е. выполнялось условие (15). Расстояние между метками можно изменять только за счёт перемещения нижней метки .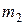

Порядок выполнения работы

1. Ознакомиться с лабораторной установкой и проверить её исправность.

2. Измерить расстояние 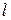 между меткам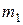и и .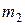

3. Измерить микрометром диаметр 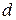 шарика и опустить этот шарик в сосуд с жидкостью.

4. В момент прохождения шарика мимо метки 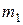 включить секундомер. При этом глаз наблюдателя должен находиться на одном уровне с меткой .

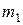5. Остановить секундомер в момент прохождения шарика мимо нижней метки 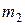. При этом глаз наблюдателя должен находиться на уровне метки .

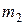6. Произвести отсчёт по секундомеру времени 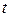 движения шарика между меткам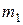и и .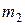

7. Повторить подобный опыт не менее пяти раз, выполняя каждый раз последовательно все пункты 2-6.

8. Температура оказывает заметное влияние на коэффициент вязкости, поэтому следует записать температуру, при которой производят опыт. Плотность шарика и плотность жидкости указаны на установке.