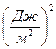1. Составить таблицу результатов измерений и наблюдений по форме (табл. 2).
Таблица 2
| Номер опыта |  ,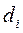
|  ,
|  ,
| 
|  ,
|  ,
|
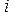
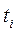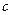
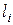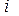
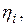
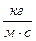
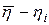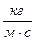
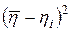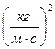
| 1 | . | . | ||||
| 5 |
2. Вычислить доверительный интервал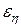 
по заданной доверительной вероятности 
:
.
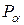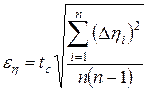3. Оценить границу абсолютной допустимой ошибки микрометра, линейки, секундомера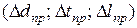 
.
4. Вычислить относительную приборную ошибку, допущенную при определении коэффициента вязкости по формуле:
,
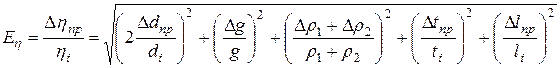где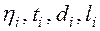 
берутся из табл. 2 и соответствуют случаю, когда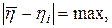 
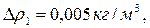
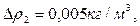
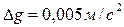при 
.
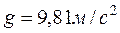5. Вычислить абсолютную приборную погрешность коэффициента вязкости:
.
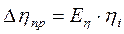6. Сравните абсолютную приборную погрешность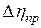 
и доверительный интервал 
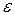. Если они одного порядка, то ошибка измерения 
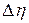вычисляется по формуле:
.
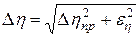Если они отличаются хотя бы на порядок, то берётся наибольшая ошибка.
7. Окончательный результат запишите в виде
.
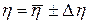8. Указать температуру, при которой производился опыт.
Контрольные вопросы
1. Дайте общую характеристику явлений переноса.
2. Как зависит сила сопротивления от скорости при ламинарном и турбулентном течениях? Почему?
3. Получите формулу (9) методом анализа размерностей.
4. Как зависит от температуры коэффициент вязкости газов? Объясните эту зависимость на основе молекулярно-кинетической теории.
5. Является ли течение жидкости в проведённом Вами опыте ламинарным или турбулентным? Объясните ответ, используя результат измерения.
6. Нужно ли вводить поправочный множитель (18) в формулу (17) в
Ваших измерениях?
7. Оцените силу сопротивления, действующую на шарик, используя результаты опыта.
8. Пользуясь табл.1, определите коэффициент вязкости сгущенного молока при t = 20° C в системе СГС (СИ)?
9. Оцените, с какой (по порядку величины) скоростью должен двигаться шарик в Вашем опыте, чтобы течение жидкости было турбулентным?
ЛАБОРАТОРНАЯ РАБОТА № 6
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПОВЕРХНОСТНОГО
НАТЯЖЕНИЯ ЖИДКОСТИ
1. Цель работы: Изучение явления поверхностного натяжения жидкостей, определение коэффициента поверхностного натяжения жидкости методом Ребиндера.
Краткая теория
Молекулы в жидкости расположены настолько близко друг к другу, что между ними возникают значительные силы взаимодействия. Известно, что силы взаимодействия молекул быстро убывают с увеличением расстояния между ними. Следовательно, силы взаимодействия между молекулами жидкости существенно больше, чем силы взаимодействия между молекулами жидкости и молекулами её пара.
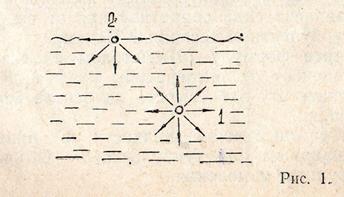Если взять (рис. 1) молекулу 1, находящуюся в глубине жидкости, то она подвержена воздействию соседних молекул со всех сторон в одинаковой мере и поэтому равнодействующая всех молекулярных сил, действующих на неё, равна нулю.
Чем ближе к поверхности молекула, тем больше и равнодействующая, направленная внутрь жидкости. Таким образом, все молекулы, лежащие у поверхности, испытывают силы, стремящиеся втянуть их внутрь жидкости. Для молекулы 2, находящейся на поверхности жидкости, силы молекулярного притяжения направлены только по касательной к поверхности и внутрь жидкости.
Силы, направленные перпендикулярно поверхности и сжимающие нижележащие слои, называются силами молекулярного давления. Силы, направленные по поверхности жидкости и стремящиеся сократить эту поверхность, называются силами поверхностного натяжения. Под влиянием этих сил поверхностный слой жидкости приходит в состояние, напоминающее растянутую упругую плёнку, стремящуюся сократиться. Для того чтобы такую плёнку удержать в равновесии, к линии её границы надо приложить силу F , касательную к поверхности жидкости, называемую силой поверхностного натяжения. Эта сила тем больше, чем больше длина границы пленки l , т. е.
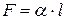(1)
или
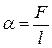, (2)
где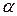 
— коэффициент поверхностного натяжения жидкости.
Таким образом, коэффициент поверхностного натяжения определяется силой поверхностного натяжения, действующей на единицу длины границы поверхности жидкости. В системе СИ коэффициент поверхностного натяжения имеет размерность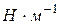 
.
Сила поверхностного натяжения всегда направлена по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует.
Зная силу поверхностного натяжения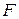 
, можно вычислить работу 
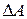, которую надо совершить, чтобы увеличить поверхность жидкости на величину 
.
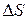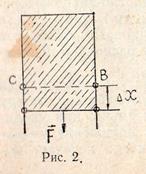
Рассмотрим рис. 2. На нём изображен проволочный прямоугольный каркас, нижняя сторона которого (проволочка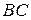 
длиной 
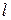) сделана подвижной. Предположим, что этот каркас заполнен мыльной плёнкой, которая представляет собой мыльную воду, имеющую два поверхностных слоя.
Под действием сил поверхностного натяжения свободная поверхность плёнки стремится сократиться. Чтобы удержать плёнку в равновесии, надо, согласно формуле (1), к проволочке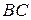 
приложить силу, которая равна
.
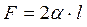Пусть граница поверхности жидкости длиной 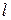передвинулась в направлении действующей силы 
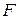на расстояние 
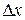. При этом будет совершена работа:
.
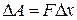С учётом выражения для силы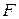 
имеем:
,
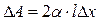или
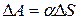, (3)
откуда
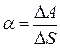, (4)
где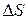 
– приращение площади свободной поверхности жидкости. Из (4) следует, что коэффициент поверхностного натяжения 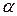определяется работой, которую необходимо затратить для увеличения поверхности жидкости на единицу площади. Таким образом, в системе СИ коэффициент поверхностного натяжения можно измерять не только в ньютонах на метр ( 
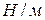), но и в джоулях на квадратный метр ( 
).
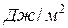Наибольшие значения коэффициента поверхностного натяжения имеют жидкости с наиболее прочными связями между их молекулами. Так, например, для ртути относительно её пара коэффициент поверхностного натяжения (при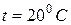 
) равен 
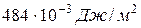, а для анилина в тех же условиях — 
.
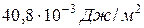Коэффициент поверхностного натяжения различен для различных жидкостей, а для одной и той же жидкости он существенно зависит от температуры жидкости (табл. 1) и наличия в ней примесей, особенно примесей поверхностно-активных веществ (жирные кислоты, их соли, спирты и др.), так как для переноса молекул этих веществ к поверхности требуется меньше энергии, чем для переноса молекул исследуемой жидкости.
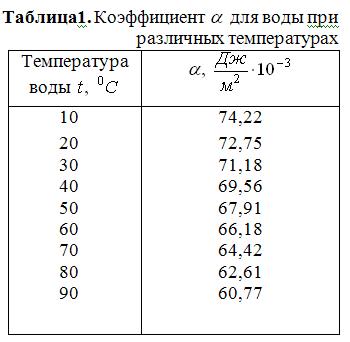Зависимость коэффициента 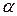от температуры объясняется тем, что при повышении температуры взаимодействие между молекулами жидкости ослабляется. Следовательно, при увеличении температуры жидкости поверхностное натяжение уменьшается. Вблизи критической температуры, когда исчезает поверхность раздела жидкость-пар, коэффициент поверхностного натяжения данной жидкости обращается в нуль.
Существует несколько методов определения коэффициента поверхностного натяжения. В основе этих методов лежат следующие закономерности.
Если поверхностный слой жидкости не плоский, а имеет кривизну, то силы поверхностного натяжения создают в таком слое избыточное давление, обусловленное кривизной поверхностного слоя. Это избыточное давление определяется формулой Лапласа:
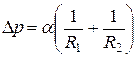, (5)
где 
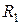и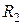 
— главные радиусы кривизны поверхности в рассматриваемой точке.
Добавочное давление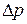 
направлено всегда к центру кривизны поверхности (в случае выпуклой поверхности жидкости дополнительное давление направлено внутрь жидкости, в случае вогнутой — наружу). Поверхность жидкости в узких трубках ( капиллярах ) называют мениском. Для смачивающей жидкости (когда силы взаимодействия между молекулами жидкости слабее взаимодействия между молекулами жидкости и твёрдого тела) мениск вогнутый. Если жидкость не смачивает твёрдое тело (сила сцепления между молекулами жидкости твёрдого тела меньше сил взаимодействия между молекулами жидкости), мениск выпуклый. В узких капиллярах поверхность мениска можно считать частью сферы, то есть можно принимать 
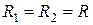. Тогда формула (5) будет иметь вид:
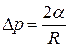. (6)
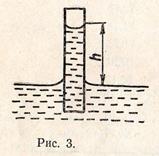Под действием отрицательного избыточного давления смачивающая жидкость поднимется по капилляру на некоторую высоту h (рис. 3), при которой избыточное Лапласово давление будет уравновешено гидрастатическим давлением поднявшегося столбика жидкости:
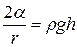, (7)
где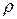 
— плотность жидкости; 
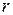— радиус капилляра;
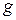— ускорение силы тяжести.
Из соотношения (7) получают формулу для определения коэффициента поверхностного натяжения:
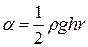. (8)
Заметим, что формула (8) справедлива только при условии полного смачивания стенок капилляра исследуемой жидкостью.
Если в верхней части капилляра, опущенного нижним концом в жидкость (рис. 3), создавать давление больше атмосферного, то поверхность жидкости внутри капилляра под воздействием этого давления начнет опускаться до тех пор, пока у нижнего конца капилляра не образуется воздушный пузырёк того же диаметра, что и диаметр капилляра. Затем, при дальнейшем увеличении давления, пузырёк отрывается от капилляра. Измеряя давление, соответствующее моменту отрыва пузырька, можно определить величину коэффициента поверхностного натяжения исследуемой жидкости. Метод определения коэффициента поверхностного натяжения жидкости путём измерения наибольшего давления пузырьков предложен академиком П. А. Ребиндером.
Существуют и другие методы определения коэффициента 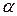, например, с помощью весов Жолли. В данной работе используется метод Ребиндера.
Описание установки
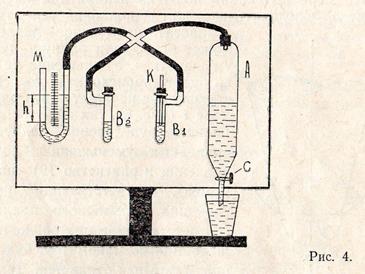Основными элементами установки для определения коэффициента поверхностного натяжения жидкости методом академика П. А. Ребиндера являются: жидкостный манометр 
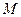, аспиратор 
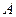, две пробирк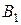и 
и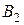 
, тонкая стеклянная трубка 
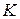с концом, оттянутым в капилляр. Схема соединения перечисленных элементов показана на рис. 4.
Перед началом опыта аспиратор 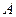(при закрытом кране) наполняется водой, в пробирку 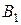наливается исследуемая жидкость (например, спирт), в пробирку 
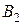— эталонная жидкость (например, дистиллированная вода). В одну из пробирок, например 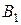, через отверстие в пробке вставляется трубочка 
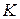так, чтобы её оттянутый под капилляр кончик едва касался бы поверхности жидкости.
Если слегка приоткрыть кран аспиратора, то вода начнёт медленно вытекать из него, и в верхней части аспиратора, а следовательно и в верхней части пробирок 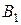и 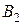, а также в правом колене манометра образуется разряжение. Давление 
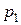над уровнями жидкости в аспираторе и пробирках будет меньше атмосферного 
:
.
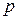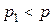В процессе дальнейшего разряжения воздуха в пробирке 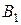поверхность жидкости на «кончике» капилляра начинает искривляться и становится частью некоторой сферы радиуса 
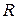(рис. 5). Начинает образовываться воздушный пузырёк. На него со стороны жидкости будет действовать дополнительное давление, определяемое формулой (6). Атмосферное давление 
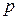будет уравновешиваться давлением воздуха 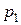, находящимся в аспираторе 
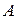и в пробирке 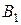и добавочным (Лапласовым) давлением 
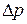. Гидростатическим давлением можно пренебречь. С учётом (6) можно записать:
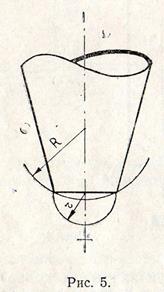
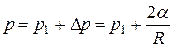. (9)
По мере вытекания воды из аспиратора уменьшается давление 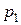. Следовательно, для выполнения условия (9), должно возрастать избыточное давление 
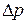. А это может быть, если радиус пузырька будет уменьшаться. Уменьшение радиуса пузырька будет происходить до тех пор, пока этот радиус не будет равен радиусу капилляра 
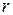(рис. 5), так как любое, даже небольшое увеличение радиуса пузырька приведёт к уменьшению дополнительного давления и равенство (9) нарушается. В момент, соответствующий равенству 
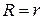, величина избыточного давления, а также соответствующая ему разность 
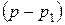, наблюдаемая по манометру, будет максимальной, и пузырек оторвётся. Далее начинается аналогичный процесс формирования нового пузырька.
Для момента отрыва пузырька от капилляра справедливо равенство:
.
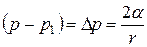Следовательно, измерив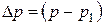 
по манометру 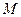и определив радиус 
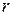капилляра, можно вычислить 
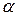. Однако с нужной точностью радиус капилляра определить трудно, поэтому обычно его из расчётной формулы исключают. Для этого вначале проводят опыт с жидкостью, коэффициент поверхностного натяжения 
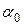которой известен, а затем повторяют опыт с исследуемой жидкостью для определения 
.
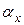Если через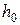 
обозначить величину максимального давления (разность высот в манометре) для эталонной жидкости, а через 
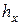- для исследуемой жидкости, то для них соответственно можно написать в момент отрыва пузырька следующие равенства:
, 
.
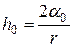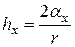Разделив одно равенство на другое, получим
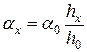. (10)
Из равенства (10) видно, что коэффициент поверхностного натяжения любой жидкости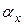 
можно определить, если известен коэффициент поверхностного натяжения другой жидкости 
.
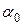В нашем опыте в качестве эталонной жидкости берётся дистиллированная вода при комнатной температуре (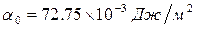 
).
Порядок выполнения работы
1. Ознакомиться с лабораторной установкой и подготовить её для проведения опыта при заданной (комнатной) температуре;
а) налить воду в аспиратор;
б) наполнить дистиллированной водой пробирку ;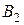
в) наполнить исследуемой жидкостью пробирку ;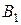
г) опустить капилляр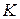 
в сосуд 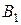настолько, чтобы его конец касался поверхности жидкости.
2. Составить таблицу результатов наблюдений по прилагаемой форме (табл. 2).
Таблица 2.
| Номер опыта | Исследуемая жидкость | Эталонная жидкость |
|
|
| ||||
| Положение уровней в манометре, мм | Положение уровней в манометре, мм | ||||||||
| левый | правый |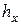 
| левый | правый |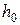
| ||||
1
2
3
…
| |||||||||
,
,
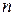
3. Медленно открывая кран аспиратора, добиться появления пузырьков на конце капилляра не группами, а по одному. Это условие необходимо для того, чтобы уровни жидкости в манометре изменялись медленно.
4. Измерить в момент выхода пузырька максимальную разность уровней жидкости 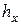в коленах манометра 
.
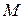5. Повторить измерения 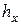не менее 7-10 раз. Результаты занести в табл. 2.
6. Переставить капилляр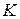 
в трубку 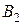и проделать столько же раз аналогичные опыты (выполнить пункты 3, 4, 5) с эталонной жидкостью (водой). Результаты измерений 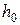занести в таблицу 2.
Примечание: при перестановке капилляра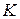 
из трубки 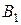в трубку 
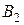его необходимо тщательно просушить.
7. Измерить и записать в свой отчёт температуру, при которой проводились опыты.
Дата: 2018-12-21, просмотров: 403.
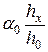
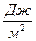
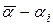
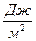
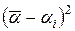
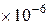