1. Записать с точностью до второго знака значения ускорения силы тяжести 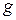 и числа  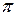и определить их предельные погрешности .

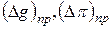2. Вычислить 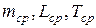, а также абсолютные погрешности .

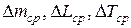3. Определить, используя расчётную формулу, наиболее вероятное значение момента инерции .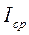

4. Вычислить среднее значение абсолютной погрешности:

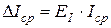
где 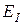 — относительная погрешность, вычисляемая по формуле:

.

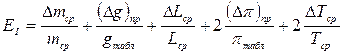Записать результаты расчётов в виде:

_{. .}

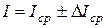6. Определить доверительную вероятность для доверительного интервала:

.

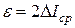7. Записать окончательный результат в следующем виде:

.

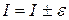8. Вычислить по теореме Штейнера (17) (используя результаты измерений и расчётов) момент инерции 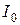 рассматриваемого маятника относительно оси, проходящей через центр масс этого маятника и параллельной оси, относительно которой данный маятник совершает колебания (рис. 4).

Задание 2. Исследование зависимости периода колебаний математического маятника от его длины.

Приборы и принадлежности : математический маятник, секундомер, линейка металлическая с ценой деления 1 мм, угольник.

При выполнении задания рекомендуется соблюдать следующую последовательность.

1. Ознакомиться с лабораторной установкой и проверить (в присутствии лаборанта) её работу.

2. Составить таблицу результатов опытов по прилагаемой форме (табл. 2).

Номер опыта	Длина маятника l, м	Число колебаний N	Продолжительность колебаний маятника в данном опыте				Период колебаний Т, с
			τ1 , с	τ2 , с	τ3 , с	τср , с
1
…

3. Установить длину маятника не менее 50 см и измерить её.

4. Отклонить маятник от положения равновесия на угол 5-10° и предоставить ему свободно колебаться.

5. Замерить с помощью секундомера время 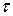 20-ти полных колебаний. Измерения  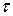повторить три раза.

6. Повторить аналогичные опыты ещё 3-4 раза, каждый раз увеличивая длину маятника на 15—20 см.

7. Записать в табл. 2 исходные данные и результаты наблюдения (длину маятника 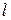, число колебаний 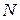, продолжительность колебаний 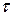) для каждого i-гo опыта.

8. Вычислить для каждого опыта период колебания математического маятника .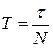

9. Построить на миллиметровой бумаге в прямоугольной системе координат теоретический график зависимости периода колебаний математического маятника от его длины, используя формулу (18).

10. Нанести на график теоретической зависимости 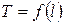 экспериментальные точки с координатами  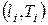из табл. 2 и соединить их плавной линией.

11. Оценить соответствие (расхождение) опытных данных с теоретической зависимостью 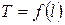 и объяснить причины возможного расхождения результатов эксперимента и теоретической кривой.

5. Контрольные вопросы

1. Какие силы называются квазиупругими?

2. Напишите дифференциальные уравнение гармонических колебаний маятника и назовите все физические величины, которые входят в данное уравнение, укажите единицы этих величин в СИ.

3. Материальная точка совершает колебания по закону 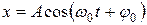. Докажите, что величина скорости и ускорения этой точки изменяется во времени по гармоническому закону и изобразите на одном рисунке графики .

4. Объясните, в чём состоит принципиальное различие между математическим и физическим маятниками.

5. Напишите формулу периода колебаний математического маятника и сформулируйте выводы, которые, по Вашему мнению, следуют из данной формулы. Сделайте то же самое для физического маятника.

6. Укажите причины возможных ошибок при прямых измерениях физических величин при выполнении заданий 1 и 2 данной лабораторной работы.

7. При какой длине 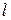 математического маятника частота  его свободных колебаний равна 0,159 Гц?

8. Какой вид будет иметь функция 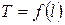 на графике в координатах ?

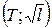ЛАБОРАТОРНАЯ РАБОТА № 5