Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

                      поперечном изгибе

Построение эпюр поперечных сил и изгибающих моментов су­щественно упрощается при использовании дифференциальных зави­симостей между изгибающим моментом, поперечной силой и интен­сивностью равномерно распределенной нагрузки (теорема Журавского):

Поперечная сила равна производной от изгибающего момента по длине балки:

                                                    

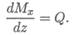
Интенсивность равномерно распределенной нагрузки равна производной от поперечной силы по длине балки:

                                                   

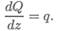
Из выше указанного следует:

если М_и = const, то Q = 0;   если Q = const; то q = 0.

            Тема 2.6. Изгиб. Классификация видов изгиба                                      245

       Контрольные  вопросы

1. Какую плоскость называют силовой?

2. Какой изгиб называют прямым? Что такое косой изгиб?

3. Какие силовые факторы возникают в сечении балки при чи­стом изгибе?

4. Какие силовые факторы возникают в сечении при поперечном
изгибе?

5. Определите поперечную силу и изгибающий момент в сечении
1-1 (рис. 29.7). Расстояние сечения от свободного конца балки 5 м.

6. Определите реакцию в опоре В.

                    

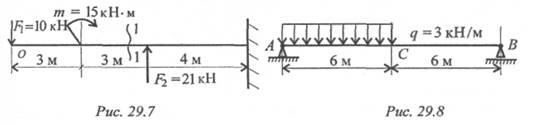
7. Определите величину поперечной силы и изгибающего момен­та в сечении С, использовав схему балки (рис. 29.8).

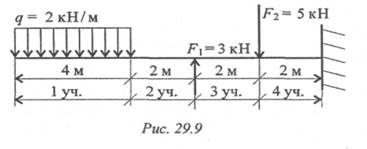
8. Определите участок чистого изгиба (рис. 29.9).

 

       

246                                                                                                                      Лекция 30

ЛЕКЦИЯ 30

Тема 2.6. Изгиб.

Построение эпюр поперечных сил

И изгибающих моментов.

Основные правила построения эпюр

Знать порядок построения и контроля эпюр поперечных сил и изгибающих моментов.

Уметь строить эпюры поперечных сил и изгибающих моментов.

Эпюры поперечных сил и изгибающих моментов можно строить, предварительно разделив балку на участки нагружения и составляя уравнения, выражающие изменения Q и М_х по участкам.

Напомним, что границы участков нагружения — это сечения, в которых приложены внешние нагрузки.

Примеры решения задач

Пример 1. На балку действуют сосредоточенные силы и мо­мент (рис. 30.1). Построить эпюры поперечных сил и изгибающих моментов.

 

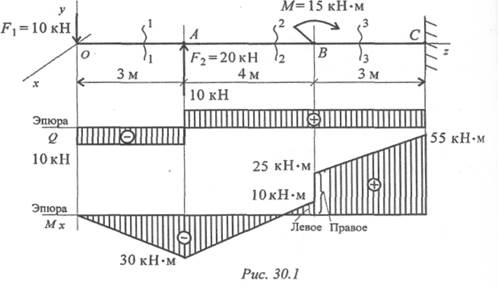
                                                                     Тема 2.6. Изгиб                                                              247

Решение

Последовательно по участкам нагружения рассматриваем вну­тренние силовые факторы в сечениях. Силовые факторы определяем из условий равновесия отсеченной части. Для каждого участка за­писываем уравнения внутренних силовых факторов.

Используем известные правила:

— поперечная сила численно равна алгебраической сумме проекций внешних сил на ось Оу;

— изгибающий момент численно равен алгебраической сумме
моментов внешних сил, действующих на отсеченную часть, относительно нейтральной оси, совпадающей с осью Ох;

— принятые знаки поперечных сил и изгибающих моментов
(рис. 30.2):

                  

               

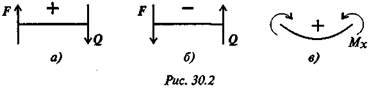
Составим уравнения равновесия.

1. Рассмотрим участок 1 (рис. 30.3а).

 

     

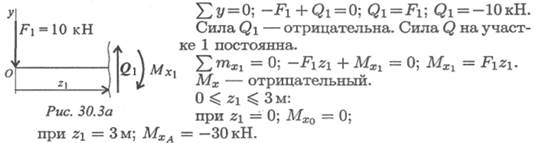
Изгибающий момент меняется по линейному закону, график -прямая линия.

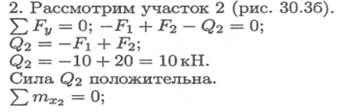
248                                                                   Лекция 30

          

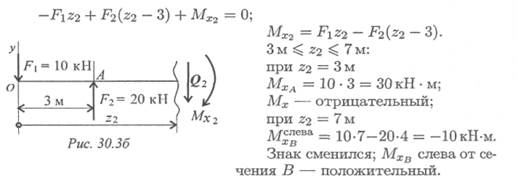
Поперечную силу и изгибающий момент можно определять сра­зу из зависимостей Q_y = ΣFy ; М_х = Σm х , не составляя уравнения равновесия участка.

Знак каждого из слагаемых этих уравнений определяем от­дельно (участок 3).

3. Рассмотрим участок 3 (рис. 30.3в).

Qз = -10 + 20 = 10 кН — поло­жительна.

Σm_Хз =0;  М_хз = - Fz ₃ + F ₂ ( z ₃ - 3) + m.

7м ≤ z ₃ ≤ 10м: при z ₃ = 7 м

MxB^справа = - 10·7+20·4+15 = 25 кН · М;

при z ₃ = 10 м.    М_хс = -10·10+20·10+15 = 55кН·м.

                                   

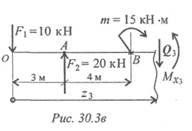
Обращаем внимание, что для точки В получено два значения изгибающих моментов: из уравнения для участка 2 левее точки В и из уравнения для участка 3 — правее точки В.

Это объясняется тем, что именно в этой точке приложен внеш­ний момент и поэтому внутренний момент сил упругости меняется.

В точках приложения внешнего момента на эпюре моментов по­явится скачок, равный величине приложенного момента.

Поперечная сила в точке В для второго и третьего участков одинакова. Следовательно, приложение внешнего момента не от­ражается на эпюре поперечных сил. График поперечной силы на участке 3 — прямая линия.

График изменения изгибающих моментов на третьем участке также прямая линия.

                                                                    Тема 2.6. Изгиб                                                               249

4. Построение эпюр. Порядок построения эпюр остается преж­ним: масштабы эпюр выбираются отдельно, исходя из значений мак­симальных сил и моментов.

Графики обводятся толстой основной линией и заштриховыва­ются поперек. На графиках указываются значения поперечных сил, изгибающих моментов и единицы измерения.

Правила построения эпюр (рис. 30.1 и 30.4):

1. Для участка, где отсутствует распределенная нагрузка, попе­речная сила постоянна, а изгибающий момент меняется по линейно­му закону.

2. В частном случае, когда поперечная сила на участке равна ну­лю, изгибающий момент постоянен (чистый изгиб), график — пря­мая линия, параллельная продольной оси (на рис. 30.1 отсутствует).

3. В том месте, где к балке приложена внешняя сосредоточенная сила, на эпюре Q возникает скачок на величину приложенной силы, а на эпюре моментов — излом.

4. В сечении, где к балке приложена пара сил (сосредоточенный момент), на эпюре М_и возникает скачок на величину момента этой пары. Поперечная сила при этом не изменяется.

5. В сечении на конце балки поперечная сила равна приложенной в этом сечении сосредоточенной силе или реакции в заделке.

6. На свободном конце балки или шарнирно опертом конце мо­мент равен нулю, за исключением случаев, когда в этом сечении приложена пара сил (внешний момент).

Пример 2. На двухопорную балку действуют сосредоточенные силы и моменты (рис. 30.4). Построить эпюры поперечных сил и изгибающих моментов.

Для двухопорной балки построение эпюр начинают с определе­ния опорных реакций балки. Для их определения используем систему уравнений равновесия, составляем  два уравнения моментов относи­тельно шарнирных опор. Затем проводим   проверку   правильности   решения   по   уравнению

n       

Σ F ky = 0 (см. лекцию 6).

0

                                                          Решение

1. Определение реакций в опорах. Уравнения равновесия:

Σ m _A = 0; -F1 · 6 + m - R_B · 10 + F ₂ · 12 = 0; -35 · 6 + 80 - R_B · 10 + 70 · 12 = 0;

250                                                                   Лекция 30

    

        

 

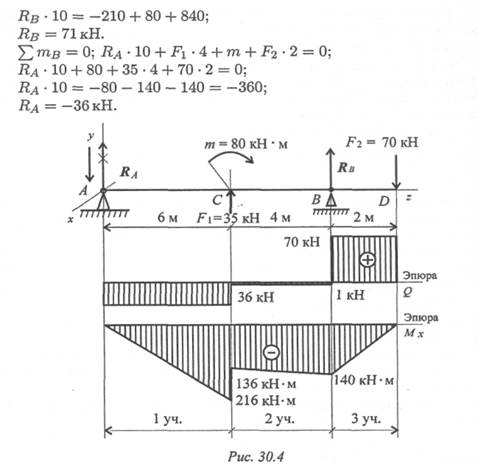
Реакция в опоре направлена в обратную сторону.

Проверка: ΣFy = 0;

- R_A + F 1 + R_B - F ₂ = 0;   -36 + 35 + 71 - 70 = 0.

Реакции определены верно.

2. Для упрощения расчетов при построении эпюр поперечных сил и изгибающих моментов можно провести расчет по характерным точкам без составления уравнений.

Для этого используют известные связи между поперечной силой и изгибающим моментом и правила построения эпюр.-

Участок 1 (от точки А до точки С).

                                                                     Тема 2.6. Изгиб                                                               251

В точке А приложена реакция Ra , направленная вниз. Попереч­ная сила на участке постоянна: Q 1 = Ra = - З6кН.

Момент в точке А равен нулю.

Точка С (слева). Приложена внешняя сила F 1 = З5кН, напра­вленная вверх, — здесь возникнет скачок вверх на величину З5кН. Момент в точке С (слева) может быть рассчитан по известной зави­симости МС^слева =- R_A · 6; МС^слева =-36·6 =-216 кН· м.

Участок 2 (от точки С справа до точки В).

Поперечная сила в точке С (справа) равна Qc = - Ra + F 1 ; Q_c = -36 + 35 = -1кН.

В точке С приложена внешняя пара сил с моментом 80кН·м, следовательно, здесь проявляется скачок на величину приложенного момента: Мc^справа = МС^слева+ m; Мc^справа = -216 + 80 = 136кН·м.

Поперечная сила на втором участке постоянна: Q2 = Qc^справа.

Момент в точке В определяется по зависимости

М B = - R_A • 10 + F1 • 4 + m; M_B = -36 • 10 + 35 • 4 + 80 = -140 кН•м.

Справа и слева от точки В момент имеет одинаковые значения.

Участок 3 (от точки В (справа) до точки D ).

В точке В приложена внешняя сила R b.  Здесь  появляется  скачок  на  величину 71 кН, Q_B = -1 + 71 = 70 кН.

Дальше по участку поперечная сила не изменяется. Момент в точке D равен нулю, т.к. здесь не приложена внешняя пара сил: M_D = 0.

Рассмотрение поперечных сил и изгибающих моментов можно было провести и справа налево.

По полученным значениям сил и моментов строим эпюры (эпю­ры под схемой вала, рис. 30.4).

        Контрольные вопросы и задания

1. Определите величины поперечных сил в сечении 1 и в сечении 2 (рис. 30.5).

      

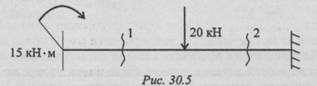
2. Напишите формулу для расчета изгибающего момента в сечении 3 (рис. 30.6).

252                                                                   Лекция 30

                    

                 

 

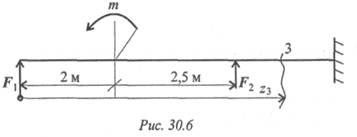
3. Из представленных эпюр выберете эпюру поперечной силы для изображенной балки (рис. 30.7).

Пояснения.

A. Обратить внимание на знак силы в сечении 1 (знак +).

Б. Обратить внимание на величину скачков в местах приложе­ния внешних сил.

B. Приложение момента пары сил не должно отражаться на
эпюре Q .

4. По рис. 30.8 выбрать эпюру изгибающего момента для изображенной на рис. 30.7 балки.

      

 

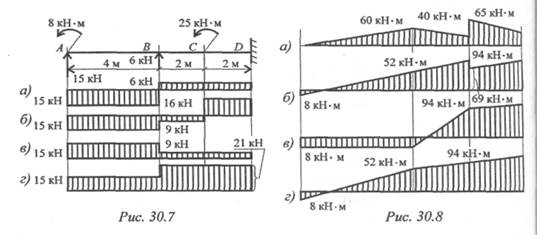
Пояснения.

A. На конце бруса приложен момент пары, следовательно, в этом
месте изгибающий момент должен быть равен этому же значению.

Б. Обратить внимание на знак момента в сечении 1.

B. В  точке   А  приложена   также   и   сила ,   поэтому линия ,   очертившая

 

                                                    

                                                                Тема 2.6. Изгиб                                                            253

 эпюру, должна быть наклонной.

5. Ответьте на вопросы тестового задания.

Тема 2.6.   Изгиб.