При изгибе. Линейные и угловые перемещения
При изгибе, их определение
Иметь представление о касательных напряжениях при изгибе, об упругой линии балки, о деформациях при изгибе и методах определения линейных и угловых перемещений.
Знать один из методов определения линейных и угловых перемещений.
Поперечный изгиб. Внутренние силовые факторы.
Напряжения
Рассмотрим изгиб балки, защемленной справа и нагруженной сосредоточенной силой F (рис. 33.1).
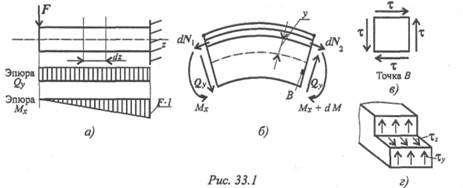
В поперечном сечении возникает изгибающий момент, меняющийся по длине балки, и постоянная поперечная сила Q .
Рассмотрим участок балки длиной dz (рис. 33.1b).
Изгибающий момент, как известно, является равнодействующим элементарных моментов, возникающих в результате действия продольных сил упругости. Связь между нормальными напряжениями в точках поперечного сечения и изгибающим моментом уже рассматривал ась:
Тема 2.6. Понятие о касательных напряжениях при изгибе 271
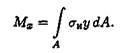
Поперечная сила представляет собой равнодействующую касательных сил упругости, возникающих в поперечных сечениях (рис. 33.1в), и связана с касательными напряжениями зависимостью
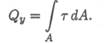
В силу парности касательных напряжений в продольных сечениях балок, параллельных нейтральному слою, возникают такие же по величине касательные напряжения (рис. 33.1г).
Появление касательных напряжений в продольных слоях балок подтверждается следующим опытом. Рассмотрим поперечный изгиб двух балок, одна — цельная, другая — составленная из нескольких положенных друг на друга слоев (рис. 33.2). Цельная балка изогнется (рис. 33.2а), брусья второй балки сдвинутся (рис. 33.26). Каждый из брусьев деформируется независимо. В цельной балке сдвигу слоев препятствуют возникающие касательные напряжения.
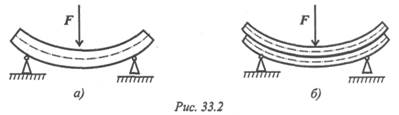
На поверхности касательные напряжения равны нулю.
Формула для расчета касательных напряжений для балки квадратного сечения была получена в 1855 году русским инженером Д. И. Журавским,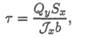 
где Qy — поперечная сила в сечении; Sx — статический момент отсеченной части относительно оси х, Sx = Аoтсyc, Аoтс — площадь поперечного сечения отсеченной части (рис. 33.3); Jx — момент инерции сечения; b— ширина балки.
272 Лекция 33
Наибольшее значение касательного напряжения достигается на нейтральной оси: 
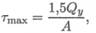А — площадь сечения.
Максимальное напряжение при поперечном изгибе в полтора раза больше среднего значения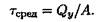 
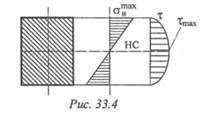Обнаруживается, что максимальные нормальные напряжения в сечении не совпадают с максимальными касательными (рис. 33.4).
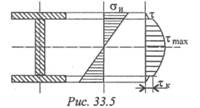
Для длинных балок расчет проводят только по нормальным напряжениям, т. к. касательные здесь не значительны. Для коротких балок, нагруженных значительными поперечными силами вблизи опор, проводят расчет по касательным напряжениям. Однако для тонкостенных профилей (двутавр, швеллер) необходимо проверять прочность балки в точках, где полка сочленяется со стенкой. Здесь и нормальные, и касательные напряжения значительны (рис. 33.5).
Понятия о линейных и угловых перемещениях
при изгибе
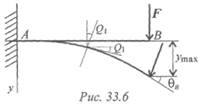
Под действием поперечных нагрузок продольная ось искривляется (рис. 33.6). Если материал подчиняется закону Гука, после снятия нагрузок брус выпрямляется, поэтому изогнутую ось бруса называют упругой линией. По форме упругой линии балки можно судить о перемещениях при изгибе.
При прямом поперечном изгибе бруса его ось, искривляясь, остается
Тема 2.6. Понятие о касательных напряжениях при изгибе 273
в силовой плоскости. В результате деформации бруса каждое из его поперечных сечений получает вертикальное и горизонтальное перемещение, а само сечение поворачивается на некоторый угол θ.
Деформации должны иметь упругий характер, они достаточно малы. В этом случае горизонтальные перемещения сечений ничтожно малы и не учитываются. Рассматривают вертикальные перемещения центра тяжести сечения, называемые прогибами (у). Максимальные прогибы обозначают f = уmax. Для обеспечения нормальной работы устанавливаемого на балках оборудования проводят расчет на жесткость.
Условие жесткости выражается неравенством
f ≤ [ f ],
где f — максимальный расчетный прогиб балки; [f] — допускаемый прогиб.
Иногда проверяется угол поворота сечения θ < [θ].
Допускаемый прогиб невелик: от 1/200 до 1/1000 пролета балки; допускаемый угол поворота 1·10-3 рад.
Существует несколько методов определения перемещений сечений при изгибе. Один из них основан на дифференцировании уравнения упругой линии, более рациональный способ — использование интегралов Мора. Метод Мора — универсальный способ определения линейных и угловых перемещений в любых системах.
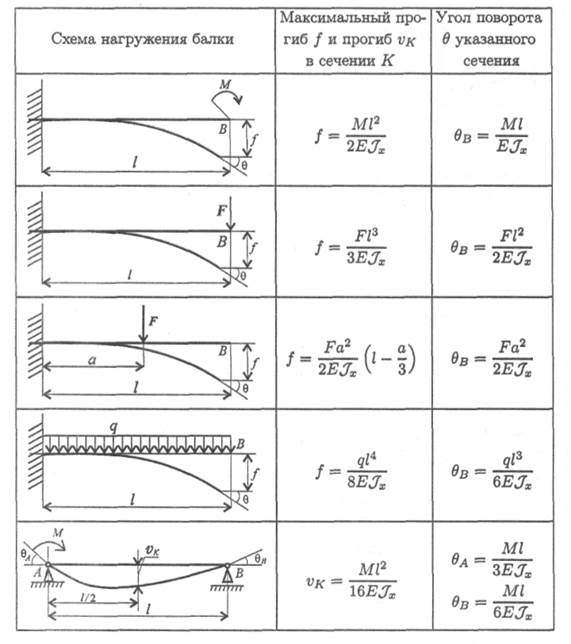
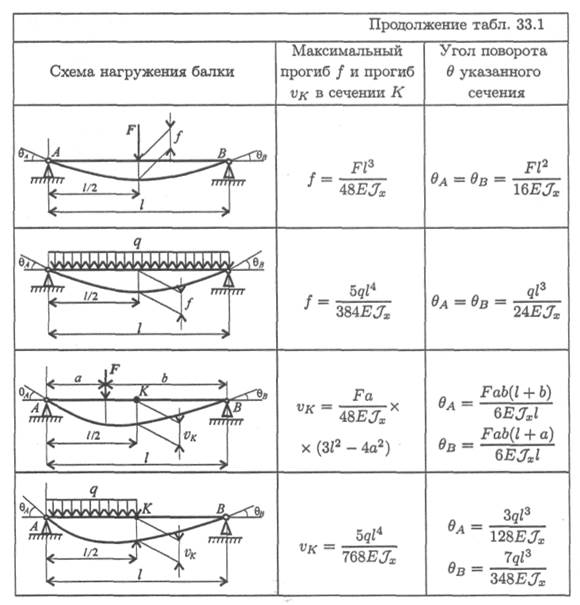
Для облегчения расчетов на жесткость можно использовать формулы прогибов и углов поворота сечений балок для простейших случаев нагружений. Наиболее распространенные случаи нагружения и расчетные формулы приведены в таблице.
При решении используем принцип независимости действия сил. Заданный случай нагружения делится на составляющие, для которых прогибы рассчитываются по известным табличным формулам, результаты расчетов суммируются.
Ограничение угла поворота вводится для обеспечения нормальной работы подшипников скольжения и роликовых подшипников.
В этом случае проверяется дополнительное условие жесткости:
274 Лекция 33
Формулы для определения прогибов и углов поворота сечений балок
Таблица 33.1
Тема 2.6. Понятие о касательных напряжениях при изгибе 275
Примеры решения задач
Проверить жесткость двутавровой балки ( рис. 33.7 ). Принять
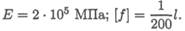Сечение балки — двутавр № 45.
Решение
Используем принцип независимости действия сил. По приведенным в
276 Лекция 33
таблице формулам рассчитываем прогиб балки в точке от каждого вида нагружения отдельно (рис. 33.7 (1, 2, 3)).
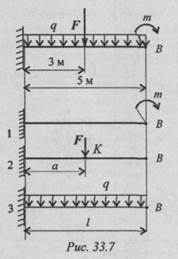Поскольку все действующие нагрузки прогибают балку вниз, результаты действия нагрузок можно сложить. Полученный суммарный прогиб сравним с допускаемым прогибом.
5000
Допускаемый прогиб [f] = ——— = 25 мм.
200
Суммарный прогиб
Исходные данные: т = 12 кН • м = 12 • 106 Н • м; а= 3 м = 3 • 103 мм;
F = 40kH = 40·103H; q = 4 кН/ м = 4 Н/мм; l = 5 м = 5 • 103 мм.
Для двутавра № 45 ГОСТ 8239-89 
Тогда
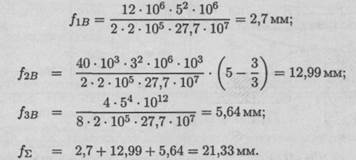
21,33 < 25 — условие жесткости выполняется. Максимальный прогиб не превышает допускаемого значения.
Тема 2.6. Понятие о касательных напряжениях при изгибе 277
Контрольные вопросы и задания
1. Какие внутренние силовые факторы возникают в сечении балки при чистом и поперечном изгибах?
2. Почему при поперечном изгибе в продольных сечениях балки
возникают касательные напряжения?
3. Каким опытом можно подтвердить возникновение касательных напряжений в продольных сечениях балки?
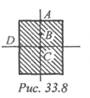
4. В какой точке поперечного сечения (рис. 33.8) касательные
напряжения при поперечном изгибе максимальны?
Варианты ответов:
1. А. 2. В. 3. С. 4. D .
5. Выберите верную эпюру распределения нормальных напряжений при изгибе (рис. 33.9). Напишите формулу для расчета нормальных напряжений при изгибе. Изгибающий момент действует в вертикальной плоскости.
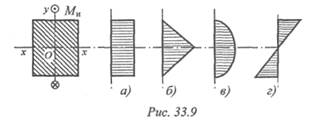
6. Как изменится максимальное нормальное напряжение в сечении (рис. 33.10а), если балку прямоугольного сечения положить плашмя (рис. 33.10б)? b = 20 мм; h = 100 мм.
7. Во сколько раз увеличится прогиб балки, если распределенную по всей длине нагрузку заменить сосредоточенной, приложенной в середине пролета? Использовать формулы для определения прогибов, приведенные в таблице 33.1.
278 Лекция 34
ЛЕКЦИЯ 34
Тема 2.7. Сочетание основных деформаций. Гипотезы прочности
Иметь представление о напряженном состоянии в точке упругого тела, о теории предельных напряженных состояний, об эквивалентном напряженном состоянии, о гипотезах прочности.
Знать формулы для эквивалентных напряжений по гипотезам наибольших касательных напряжений и энергии формоизменения.
Напряженное состояние в точке
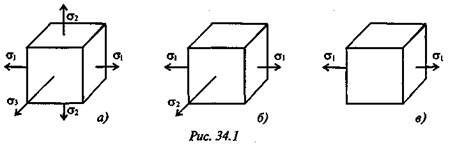
Напряженное состояние в точке характеризуется нормальными и касательными напряжениями, возникающими на всех площадках (сечениях), проходящих через данную точку. Обычно достаточно определить напряжения на трех взаимно перпендикулярных площадках, проходящих через рассматриваемую точку. Точку принято изображать в виде маленького элемента в форме параллелепипеда (рис. 34.1).
Положения теории напряженного состояния:
1. Напряженное состояние в данной точке полностью определено, если известны напряжения по любым трем взаимно перпендикулярным площадкам.
2. Среди множества площадок, которые можно провести через данную точку, есть три такие взаимно перпендикулярные площадки, на которых отсутствуют касательные напряжения, эти площадки называются главными, а нормальные напряжения, возникающие на них, называются главными напряжениями: σ 1 ; σ 2 ; σ3 (рис. 34.1).
Одно из этих напряжений — максимально, одно — минимально. Максимальное обозначают σ1, минимальное — σ3 .
Классификация видов напряженного состояния производится по главным напряжениям:
— если все три главных напряжения не равны нулю, то напряженное состояние называют объемным (трехосным) (рис. 34.1а);
— если одно из главных напряжений равно нулю, напряженное состояние называют плоским (двухосным) (рис. 34.1б);
— если два из главных напряжений ( σ2 = 0 ) противоположны
Тема 2.7. Сочетание основных деформаций 279
по знаку, напряженное состояние называют упрощенным плоским состоянием;
— если лишь одно из главных напряжений не равно нулю, напряженное состояние линейное (рис. 34.1в).
Понятие о сложном деформированном состоянии
Совокупность деформаций, возникающих по различным направлениям и в различных плоскостях, проходящих через точку, определяют деформированное состояние в этой точке.
Сложное деформированное состояние возникает, если деталь одновременно подвергается нескольким простейшим нагружениям.
Такие состояния возникают в заклепочных соединениях (срез и смятие), в болтовых соединениях (растяжение и скручивание), при поперечном изгибе бруса (изгиб и сдвиг).
Часто одним из нагружений (незначительным) пренебрегают.
Например, длинные балки рассчитывают только на изгиб.
В ряде случаев нормальные и касательные напряжения, возникающие в детали, имеют одинаковый порядок и ими нельзя пренебрегать. Тогда расчет проводят при сложном деформированном состоянии.
Сложность расчета заключается в отсутствии экспериментальных данных о предельных напряжениях, т. к. провести испытания из-за множества вариантов нагружения практически невозможно.
Для упрощения расчетов в этом случае применяют теории прочности. Смысл теорий заключается в замене реального сложного деформированного состояния равноопасным простым.
Опасное состояние может быть вызвано различными факторами: нормальные напряжения могут достигнуть предела текучести
280 Лекция 34
или предела прочности, касательные напряжения могут достигнуть опасного значения или накопленная энергия деформирования может стать слишком большой и вызвать разрушение.
Универсального критерия, позволяющего рассчитать предельное состояние для любого материала, нет. Разработано несколько различных гипотез предельных состояний, при расчетах используют наиболее подходящую гипотезу. Расчеты по гипотезам прочности позволяют избегать дорогостоящих испытаний конструкции.
В настоящее время для расчета валов при совместном действии изгиба и кручения используют только третью и пятую теории прочности.
Сравнение разнотипных состояний производится с помощью эквивалентного {простого) напряженного состояния. Обычно сложное напряженное состояние заменяют простым растяжением (рис. 34.2).
Расчетное напряжение, соответствующее выбранному одноосному растяжению, называют эквивалентным напряжением (рис. 34.26).
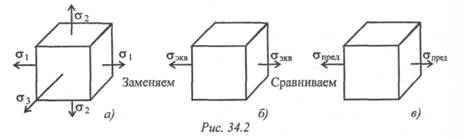
Полученное расчетным путем эквивалентное напряжение для точки сравнивают с предельным (рис. 34.2в).
Напряженное состояние в точке равноопасно эквивалентному напряженному состоянию. Условие прочности получим, сопоставив эквивалентное напряжение с предельным, полученным экспериментально для выбранного материала:
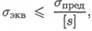где [ s ] — допускаемый запас прочности.
Как известно, предельным напряжением для пластичных материалов является предел текучести σт, а для хрупкого — предел прочности σв. Предельное напряженное состояние у пластичных материалов
Тема 2.7. Сочетание основных деформаций 281
наступает в результате пластических деформаций, а у хрупких — в результате разрушения.
Для пластичных материалов расчет может выполняться по гипотезе максимальных касательных напряжений: два напряженных состояния равноопасны, если максимальные касательные напряжения у них одинаковы (третья теория прочности).
Расчет можно проводить и по теории потенциальной энергии формоизменения: два напряженных состояния равноопасны, если энергия формоизменения у них одинакова (пятая теорема прочности).
Для хрупких и хрупко-пластичных материалов применяют теорию прочности Мора.
Расчет эквивалентного напряжения для точки по теории максимальных касательных напряжений выполняется по формуле
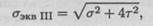
а по теории энергии формоизменения по формуле
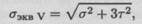
где σ — действующее в точке нормальное напряжение; τ — действующее в точке касательное напряжение.
Расчет круглого бруса на изгиб с кручением
В случае расчета круглого бруса при действии изгиба и кручения (рис. 34.3) необходимо учитывать нормальные и касательные напряжения, т. к. максимальные значения напряжений в обоих случаях возникают на поверхности. Расчет следует вести по теории прочности, заменяя сложное напряженное состояние равноопасным простым.
282 Лекция 34
Максимальное напряжение кручения в сечении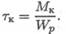 
Максимальное напряжение изгиба в сечении 
По одной из теорий прочности в зависимости от материала бруса рассчитывают эквивалентное напряжение для опасного сечения и проверяют брус на прочность, используя допускаемое напряжение изгиба для материала бруса.
Для круглого бруса моменты сопротивления сечения следующие:
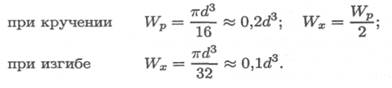
При расчете по третьей теории прочности, теории максимальных касательных напряжений, эквивалентное напряжение рассчитывается по формуле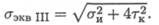 
Теория применима для пластичных материалов. При расчете по теории энергии формоизменения эквивалентное напряжение рассчитывается по формуле
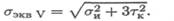
Теория применима для пластичных и хрупких материалов. Эквивалентное напряжение при расчете по теории максимальных касательных напряжений:
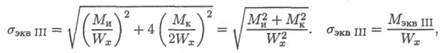
где Мэкв III = √М и² + М к² — эквивалентный момент.
Условие прочности:
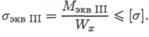
Тема 2.7. Сочетание основных деформаций 283
Эквивалентное напряжение при расчете по теории энергии формоизменения:
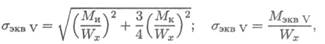
где Мэкв v = √М и² + 0,75М к² — эквивалентный момент.
Условие прочности:
Примеры решения задач
Для заданного напряженного состояния (рис. 34.4), пользуясь гипотезой максимальных касательных напряжений, вычислить коэффициент запаса прочности, если σт = 360 Н/мм .
Контрольные вопросы и задания
1. Чем характеризуется и как изображается напряженное состояние в точке?
2. Какие площадки и какие напряжения называют главными?
3. Перечислите виды напряженных состояний.
4. Чем характеризуется деформированное состояние в точке?
5. В каких случаях возникают предельные напряженные состояния у пластичных и хрупких материалов?
6. Что такое эквивалентное напряжение?
7. Поясните назначение теорий прочности.
8. Напишите формулы для расчета эквивалентных напряжений при расчетах по теории максимальных касательных напряжений и теории энергии формоизменения. Поясните, как ими пользоваться.
284 Лекция 35
ЛЕКЦИЯ 35
Тема 2.7. Расчет бруса круглого поперечного
сечения при сочетании основных деформаций
Знать формулы для эквивалентных напряжений по гипотезам наибольших касательных напряжений и энергии формоизменения.
Уметь рассчитывать брус круглого поперечного сечения на прочность при сочетании основных деформаций.
Формулы для расчета эквивалентных напряжений
Эквивалентное напряжение по гипотезе максимальных касательных напряжений σэкв = √σ2 + 4τ2.
Эквивалентное напряжение по гипотезе энергии формоизменения
σэкв = √σ2 + 3τ2,
где τ = MK / WP — расчетное касательное напряжение;
σ = M И / WX — расчетное нормальное напряжение.
Условие прочности при совместном действии изгиба
И кручения
Мэкв
σэкв = ------ ≤ [σ] ,
Wx
где Мэкв — эквивалентный момент.
Эквивалентный момент по гипотезе максимальных касательных
напряжений Мэкв III = √М и² + М к².
Эквивалентный момент по гипотезе энергии формоизменения
Мэкв v = √М и² + 0,75М к².
Особенность расчета валов
Большинство валов испытывают сочетание деформаций изгиба и кручения. Обычно валы — прямые брусья с круглым или кольцевым сечением. При расчете валов касательные напряжения от действия поперечных сил не учитывают из-за их незначительности.
Тема 2.7. Расчет бруса круглого поперечного сечения 285
Расчеты проводят по опасным поперечным сечениям. При пространственном нагружении вала пользуются гипотезой независимости действия сил и изгибающие моменты рассматривают в двух взаимно перпендикулярных плоскостях, а суммарный изгибающий момент определяют геометрическим суммированием.
Примеры решения задач
Пример 1. В опасном поперечном сечении круглого бруса возникают внутренние силовые факторы (рис. 35.1) Мх; Му; Mz .
Мх и Му — изгибающие моменты в плоскостях уОх и zOx соответственно; Mz — крутящий момент. Проверить прочность по гипотезе наибольших касательных напряжений, если [σ] = 120 МПа. Исходные данные: Мх = 0,9 кН∙м; Му = 0,8 кН•м; Mz = 2,2 кН • м; d = 60 мм.
Решение
Строим эпюры нормальных напряжений от действия изгибающих моментов относительно осей Ох и Оу и эпюру касательных напряжений от кручения (рис. 35.2).
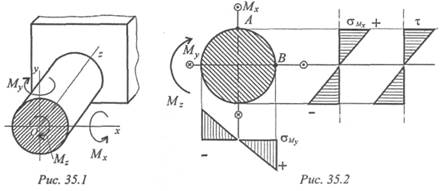
Максимальное касательное напряжение возникает на поверхности. Максимальные нормальные напряжения от момента Мх возникают в точке А, максимальные нормальные напряжения от момента Му в точке В. Нормальные напряжения складываются, потому что изгибающие моменты во взаимно перпендикулярных плоскостях геометрически суммируются.
286 Лекция 35
Суммарный изгибающий момент: Ми = √М x² + М y²;
Ми = √0,92 + 0,82 = 1,2 кН • м.
Рассчитываем эквивалентный момент по теории максимальных касательных напряжений:
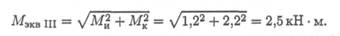
Условие прочности: Мэкв
σэкв = --------- ≤ [σ] , Wосевое = Wх = Wу.
Wосевое
Момент сопротивления сечения: Woceeoe = 0,1 • 603 = 21600 мм3.
Проверяем прочность: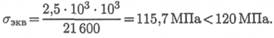 
Прочность обеспечена.
Пример 2. Из условия прочности рассчитать необходимый диаметр вала. На валу установлены два колеса. На колеса действуют две окружные силы F t 1 = 1,2 кН; Ft 2 = 2 кН и две радиальные силы в вертикальной плоскости Fr1 = 0,43 кН; Fr 2 = 0,72 кН (рис. 35.3). Диаметры колес соответственно равны d 1 = 0,1м; d2 = 0,06м.
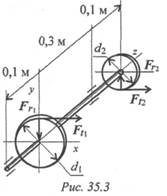Принять для материала вала [σ] = 50МПа.
Рассчитать размеры вала кольцевого сечения при с = 0,8 (с = dВН / d). Расчет провести по гипотезе максимальных касательных напряжений. Весом вала и колес пренебречь.
Решение
Указание. Используем принцип независимости действия сил, составляем расчетные схемы вала в вертикальной и горизонтальной плоскостях. Определяем реакции в опорах в горизонтальной и вертикальной плоскостях в отдельности. Строим эпюры изгибающих моментов (рис. 35.4). Под действием окружных сил вал скручивается. Определяем действующий на валу крутящий момент.
Тема 2.7. Расчет бруса круглого поперечного сечения 287
Составим расчетную схему вала (рис. 35.4).
1. Крутящий момент на валу:
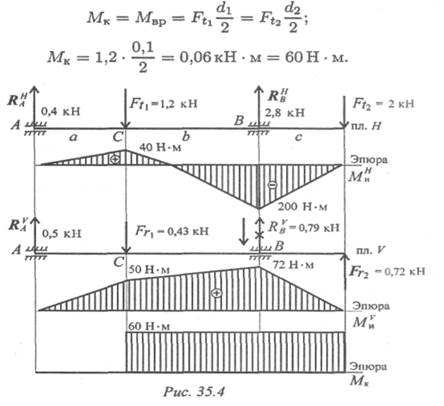
2. Изгиб рассматриваем в двух плоскостях : горизонтальной (пл. Н) и вертикальной (пл. V).
В горизонтальной плоскости определяем реакции в опоре:
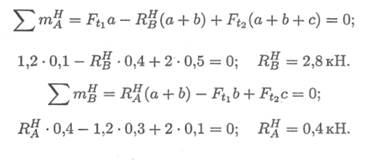
288 Лекция 35
Определяем изгибающие моменты в точках С и В:
Н Н
Мс = 400 • 0,1 = 40Н • м; М В = -2000 • 0,1 = 200Н • м.
В вертикальной плоскости определяем реакции в опоре:
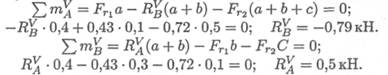
Определяем изгибающие моменты в точках С и В:
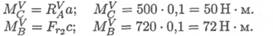
Суммарные изгибающие моменты в точках С и В:
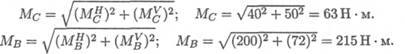
В точке В максимальный изгибающий момент, здесь же действует и крутящий момент.
Расчет диаметра вала ведем по наиболее нагруженному сечению.
3. Эквивалентный момент в точке В по третьей теории
прочности
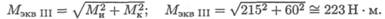
4. Определяем диаметр вала круглого поперечного сечения из
условия прочности
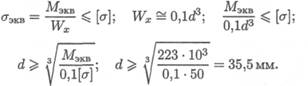
Округляем полученную величину: d — 36 мм.
Примечание. При выборе диаметров вала пользоваться стандартным рядом диаметров (Приложение 2).
5. Определяем необходимые размеры вала кольцевого сечения
dВН
при с = 0,8; с = — , где d — наружный диаметр вала.
d
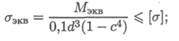
Тема 2.7. Расчет бруса круглого поперечного сечения 289
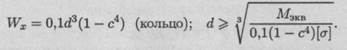
Диаметр вала кольцевого сечения можно определить по формуле
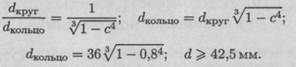
Примем d = 42 мм.
Перегрузка незначительная. dBH = 0,8 d = 0,8 • 42 = 33,6 мм.
Округляем до значения dBH = 33 мм.
6. Сравним затраты металла по площадям сечения вала в обоих случаях.
Площадь поперечного сечения сплошного вала
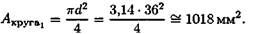
Площадь поперечного сечения полого вала
Площадь поперечного сечения сплошного вала почти в два раза больше вала кольцевого сечения:
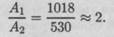
Контрольные вопросы и задания
1. Какое напряженное состояние возникает в поперечном сечении вала при совместном действии изгиба и кручения?
2. Напишите условие прочности для расчета вала.
3. Напишите формулы для расчета эквивалентного момента при расчете по гипотезе максимальных касательных напряжений и гипотезе энергии формоизменения.
4. Как выбирается опасное сечение при расчете вала?
290 Лекция 36
ЛЕКЦИЯ 36
Тема 2.10. Устойчивость сжатых стержней.
Основные положения
Иметь представление об устойчивых и неустойчивых формах равновесия, критической силе и коэффициенте запаса устойчивости, о критическом напряжении, гибкости стержня и предельной гибкости.
Знать условие устойчивости сжатых стержней, формулу Эйлера и эмпирические формулы для расчета критической силы и критического напряжения.
Понятие об устойчивом и неустойчивом равновесии
Относительно короткие и массивные стержни рассчитывают на сжатие, т. к. они выходят из строя в результате разрушения или остаточных деформаций. Длинные стержни небольшого поперечного сечения под действием осевых сжимающих сил изгибаются и теряют равновесие. Такие стержни работают на изгиб и сжатие.
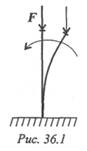Равновесие считают устойчивым, если за счет сил упругости после снятия внешней отклоняющей силы стержень восстановит первоначальную форму (рис. 36.1).
Если упругое тело после отклонения от равновесного положения не возвращается к исходному состоянию, то говорят, что произошла потеря устойчивости, а равновесие было неустойчивым.
Потерю устойчивости под действием центрально приложенной продольной сжимающей силы называют продольным изгибом.
На устойчивость равновесия влияет величина сжимающей силы.
Наибольшее значение сжимающей силы, при которой прямолинейная форма стержня сохраняет устойчивость, называют критической силой. Даже при небольшом превышении критического значения силы стержень недопустимо деформируется и разрушается.
Тема 2.10. Устойчивость сжатых стержней 291
Расчет на устойчивость
Расчет на устойчивость заключается в определении допускаемой сжимающей силы и в сравнении с ней силы действующей:
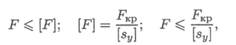
где F — действующая сжимающая сила;
[ F ] — допускаемая сжимающая сила, обеспечивает некоторый запас устойчивости;
Fкр — критическая сила;
[ s y ] — допускаемый коэффициент запаса устойчивости.
Обычно для сталей [ sy ] = 1,8 : 3; для чугуна [ sy ] = 5; для дерева [ sy ] ≈ 2,8.
Способы определения критической силы
Расчет по формуле Эйлера
Задачу определения критической силы математически решил Л.Эйлер в 1744 г.
Для шарнирно закрепленного с обеих сторон стержня (рис. 36.2) формула Эйлера имеет вид
где Е — модуль упругости;
Jmin — минимальный осевой момент инерции стержня;
l — длина стержня.
Потеря устойчивости происходит в плоскости наименьшей жесткости, поэтому в формулу входит минимальный из осевых моментов инерции сечения ( JX или Jy).
Формулу распространили на другие формы закрепления стержней, рассмотрев форму потери устойчивости в каждом случае.
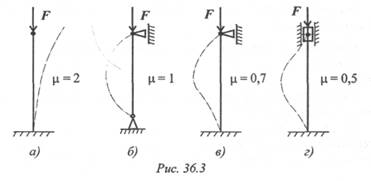
Длина стержня заменяется ее приведенным значением, учитывающим форму потери устойчивости в каждом случае: lПрив = μ l, где μ — коэффициент приведения длины, зависящий от способа закрепления стержня (рис. 36.3).
292 Лекция 36
Формула для расчета критической силы для всех случаев
Критические напряжения.
Критическое напряжение — напряжение сжатия, соответствующее критической силе.
Напряжение от сжимающей силы определяется по формуле
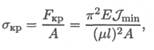
где σкр — напряжение сжатия, при котором стержень еще устойчив. Корень квадратный из отношения минимального момента инерции сечения к площади поперечного сечения принято называть минимальным радиусом инерции imin:
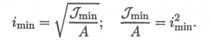
Тогда формула для расчета критического напряжения перепишется в виде
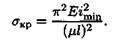
Отношение μ l / imin носит название гибкости стержня λ.
Гибкость стержня — величина безразмерная, чем больше гибкость, тем меньше напряжение:
Тема 2.10. Устойчивость сжатых стержней 293
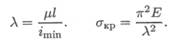
Заметим, что гибкость не зависит от материала, а определяется только геометрией стержня.
Дата: 2018-12-21, просмотров: 1357.
