Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Иметь представление о физическом смысле и порядке опре­деления осевых, центробежных и полярных моментов инерции, о главных центральных осях и главных центральных моментах инерции.

Знать формулы моментов инерции простейших сечений, спо­собы вычисления моментов инерции при параллельном переносе осей.

При растяжении, сжатии, смятии и сдвиге деталь сопротивля­ется деформации всем сечением одинаково. Здесь геометрической ха­рактеристикой сечения является площадь.

При кручении и изгибе сечение сопротивляется деформации не одинаково, при расчетах напряжений появляются другие геометри­ческие характеристики сечения, влияющие на сопротивления сече­ния деформированию.

Статический момент площади сечения

Рассмотрим произвольное сечение (рис. 25.1).

                                              

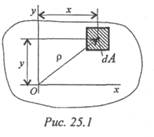
Если разбить сечение на бесконечно малые площадки dA и умножить каждую площадку на расстояние до оси координат и проинтегрировать полученное выраже­ние, получим статический момент площади сечения:

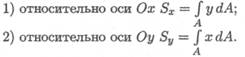
Для симметричного сечения статические моменты каждой по­ловины площади равны по величине и имеют разный знак. Следова­тельно, статический момент относительно оси симметрии равен нулю.

Статический момент используется при определении положения

               Тема 2.4. Геометрические характеристики плоских сечений                   209

центра тяжести сечения:

               

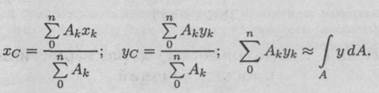
Формулы для определения положения центра тяжести можно за­писать в виде 

                                       

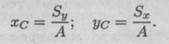
         Центробежный момент инерции

Центробежным моментом инерции сечения называется взятая по всей площади сумма произведений элементарных площадок на обе координаты:      

                                             

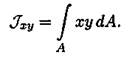
Центробежный момент инерции может быть положительным, отрицательным и равным нулю. Центробежный момент инерции от­носительно осей, проходящих через центр тяжести сечения, равен нулю.

Оси, относительно которых центробежный момент равен нулю, называются главными. Главные оси, проходящие через центр тяже­сти, называют главными центральными осями сечения.

         Осевые   моменты инерции

Осевым моментом инерции сечения относительно некоторой оси, лежащей в этой же плоскости, называется взятая по всей пло­щади сумма произведений элементарных площадок на квадрат их расстояния до этой оси:

1) осевой момент инерции сечения относительно оси Ох

210                                                                                    Лекция 25

        Полярный момент инерции сечения

Полярным моментом инерции сечения относительно некоторой точки (полюса) называется взятая по всей площади сумма произве­дений элементарных площадок на квадрат их расстояния до этой точки:

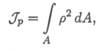где р — расстояние до полюса (центра поворота) (рис. 25.1).

Поскольку р ² = х² + у², получим: полярный момент инерции сечения равен сумме осевых: 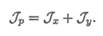Осевые моменты инерции характеризуют сопротивление сече­ния повороту относительно соответствующей оси.

Полярный момент инерция характеризует сопротивление сече­ния повороту вокруг полюса (начала координат). Единицы измере­ния моментов инерции: м⁴; см⁴; мм⁴.

        Моменты инерции простейших сечений

Осевые моменты инерции прямоугольника (рис. 25.2)

                                         

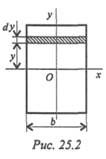
Представим прямоугольник высотой h и ши­риной b в виде сечения, составленного из бесконеч­но тонких полос. Запишем площадь такой полосы: bdy = dA . Подставим в формулу осевого момента  инерции относительно оси Ох:          

                      

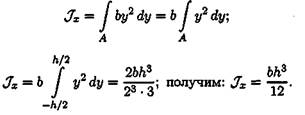
По аналогии, если разбить прямоугольник на вертикальные по­лосы, рассчитать площади полос и подставить в формулу для осе­вого момента инерции относительно оси Оу, получим:

                                     Тема 2.4. Геометрические характеристики плоских сечений                               211

                 

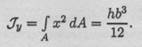
Очевидно, что при h > b сопротивление повороту относительно оси Ох больше, чем относительно Оу.

Для квадрата: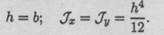

                          Полярный  момент   инерции  круга

Для круга вначале вычисляют поляр­ный момент инерции, затем — осевые.

Представим круг в виде совокупности бесконечно тонких колец (рис. 25.3).

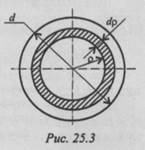Площадь каждого кольца можно рас­считать как площадь прямоугольника с длинной стороной, равной длине соответ­ствующей окружности, и высотой, равной толщине кольца: dA = 2 πp dp .

Подставим это выражение для площа­ди в формулу для полярного момента инерции: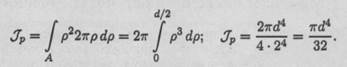           

Получим формулу для расчета полярного момента инерции круга:

               

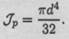
Подобным же образом можно получить формулу для расчета полярного момента инерции кольца:

                                              

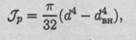
где d — наружный диаметр кольца; d_BH — внутренний диаметр ко­льца.

Если обозначить d_BH/ d = с, то

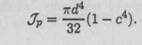
212                                                                 Лекция 25

         Осевые моменты инерции круга и кольца

Используя известную связь между осевыми и полярными момен­тами инерции, получим:

   

      

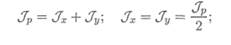
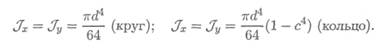
      Моменты инерции относительно параллельных осей

Оси Ox0 и Ох параллельны (рис. 25.4).

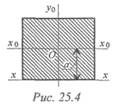При параллельном переносе прямоугольной системы осей уоО хо в новое положение уоО х зна­чения моментов инерции J_x , J_y , J_xy заданно­го сечения меняются. Задается формула перехода без вывода.

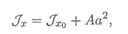здесь J_x — момент инерции относительно оси Ох;

                                  J_X0 — момент инерции относительно оси Ox0;  

 А — площадь сечения;

а — расстояние между осями Ох и Ox0.

            Главные оси и главные моменты инерции

Главные оси — это оси, относительно которых осевые момен­ты инерции принимают экстремальные значения: минимальный и максимальный.

Главные центральные моменты инерции рассчитываются отно­сительно главных осей, проходящих через центр тяжести.

Примеры решения задач

Пример 1. Определить величину осевых моментов инерции плоской фигуры относительно осей Ох и Оу (рис. 25.5).

                  Тема 2.4. Геометрические характеристики плоских сечений                     213

                                                                                                                                                                                                                     

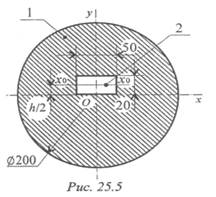                                                                                                     Решение

   1. Определим осевой момент инерции относительно оси Ох. Ис­пользуем формулы для главных центральных моментов. Предста­вим момент инерции сечения как разность моментов инерции круга и прямоугольника.

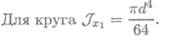            bh ³

   Для прямоугольника J_X02 = ——.

                                                                                                                   12

Для прямоугольника ось Ох не проходит через ЦТ.

Момент инерции прямоугольника относительно оси Ох:

             

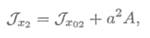
где А — площадь сечения; а — расстояние между осями Ох и Ox0 .

            

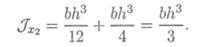
Момент инерции сечения

           

       

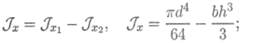
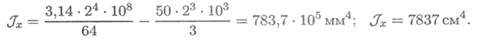
2. Осевой момент инерции относительно оси Оу:

            

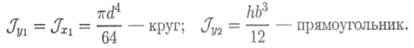
Момент инерции сечения

               

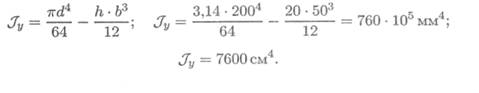
214                                                              Лекция 25

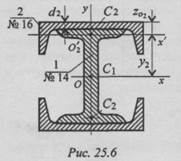
Пример 2. Найти главный центральный момент инерции сече­ния относительно оси Ох (рис. 25.6).

                                       Решение

     1. Сечение составлено из стандарт­ных профилей, главные центральные моменты инерции которых приводятся в таблицах ГОСТ, см. Приложение 1.

    Для двутавра № 14 по ГОСТ 8239-89 Jo_{x 1} = 572 см⁴.

    Для швеллера № 16 по ГОСТ 8240-89 J o x ₂ = 757 см⁴.

    Площадь А 2 = 18,1 см², J o y ₂ = 63,3 см⁴.

2. Определяем координату центра тяжести швеллера относительно оси Ох. В заданном сечении швеллер повернут и поднят.
При этом главные центральные оси поменялись местами.

y2 = ( h 1 /2) + d 2 — z o ₂ ; по ГОСТ находим h 1 = 14 см; d2 = 5 мм; zo = 1,8 см.

3. Момент инерции сечения равен сумме моментов инерции
швеллеров и двутавра относительно оси Ох. Используем формулу
моментов инерции относительно параллельных осей:

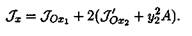В данном случае J ´ q _X2 = J ´ qу₂  =  63,3 см⁴;

y2 = (14/2) + 0,5 — 1,8 = 5,7 см (расстояние между осями координат Ох' и Ох);

            

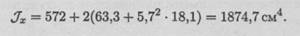
Контрольные вопросы и задания

1. Диаметр сплошного вала увеличили в 2 раза. Во сколько раз
увеличатся осевые моменты инерции?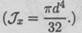

2. Осевые моменты сечения равны соответственно J_x = 2,5 мм⁴ и Jy = 6,5 мм. Определите полярный момент сечения.

3. Осевой момент инерции кольца относительно оси Ох J_x = 4 см⁴. Определите величину J_p .

                Тема 2.4. Геометрические характеристики плоских сечений                   215

 

4. В каком случае J_x наименьшее (рис. 25.7)?

        

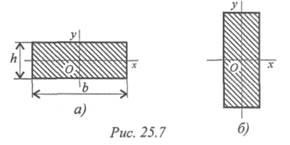
5. Какая из приведенных формул для определения J_x подойдет
для сечения, изображенного на рис. 25.8?

               

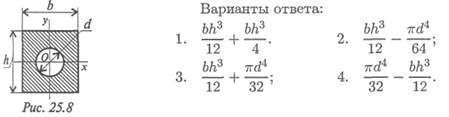
6. Момент инерции швеллера № 10 относительно главной центральной оси J_Xo = 174см⁴; площадь поперечного сечения 10,9 см².

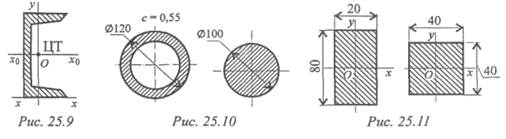
Определите осевой момент инерции относительно оси, проходя­щей через основание швеллера (рис. 25.9).

7. Сравнить полярные моменты инерции двух сечений, имею­щих практически одинаковые площади (рис. 25.10).

8. Сравнить осевые моменты инерции относительно оси Ох пря­моугольника и квадрата, имеющих одинаковые площади (рис. 25.11).

 

          

216                                                                   Лекция 26

ЛЕКЦИЯ 26

                       

                          Тема 2.5.   Кручение.  

Внутренние силовые   факторы  при   кручении.

      Построение   эпюр крутящих   моментов

Иметь представление о деформациях при кручении, о внутрен­ них силовых факторах при кручении.

Уметь строить эпюры крутящих моментов.

Деформации при кручении

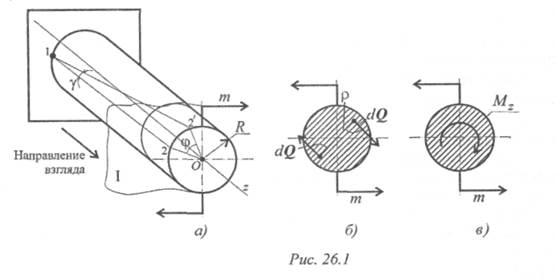
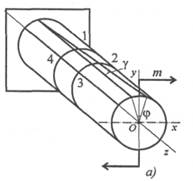
Кручение круглого бруса происходит при нагружении его па­рами сил с моментами в плоскостях, перпендикулярных продольной оси. При этом образующие бруса искривляются и разворачиваются на угол γ называемый углом сдвига (угол поворота образующей). Поперечные сечения разворачиваются на угол φ , называемый углом закручивания (угол поворота сечения, рис. 26.1).

Длина бруса и размеры поперечного сечения при кручении не изменяются.

                             

                Тема 2.5. Кручение. Внутренние силовые факторы при кручении                     217

 

Связь  между угловыми   деформациями  определяется   соотноше­нием

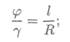                              l— длина бруса; R — радиус сечения.

Длина бруса значительно больше радиуса сечения, следователь­но, φ » γ.

Угловые деформации при кручении рассчитываются в радиа­нах.

Гипотезы при кручении

1. Выполняется гипотеза плоских сечений: поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформа­ции остается плоским и перпендикулярным продольной оси.

2. Радиус, проведенный из центра поперечного сечения бруса, после деформации остается прямой линией (не искривляется).

3. Расстояние между поперечными сечениями после деформации не меняется. Ось бруса не искривляется, диаметры поперечных се­чений не меняются.

               Внутренние силовые факторы при кручении

Кручением называется нагружение, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — крутящий момент.

Внешними нагрузками также являются две противоположно на­правленные пары сил.

Рассмотрим внутренние силовые факторы при кручении круг­лого бруса (рис. 26.1).

Для этого рассечем брус плоскостью I и рассмотрим равновесие отсеченной части (рис. 26.1а). Сечение рассматриваем со стороны отброшенной части.

Внешний момент пары сил разворачивает участок бруса про­тив часовой стрелки, внутренние силы упругости сопротивляются повороту. В каждой точке сечения возникает поперечная сила dQ (рис. 26.16). Каждая точка сечения имеет симметричную, где возни­кает поперечная сила, направленная в обратную сторону. Эти   силы образуют   пару   с   моментом    dm = pdQ ; p  —  расстояние  от  точки

218                                                                 Лекция 26

до центра сечения. Сумма поперечных сил в сечении равна нулю: . ΣdQ = 0.

С помощью интегрирования получим суммарный момент сил упругости, называемый крутящим моментом:

              

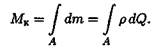
Практически крутящий момент определяется из условия равно­весия отсеченной части бруса.

Крутящий момент в сечении равен сумме моментов внешних сил, действующих на отсеченную часть (рис. 26.1в):

                   

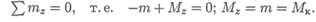
          Эпюры крутящих моментов

Крутящие моменты могут меняться вдоль оси бруса. После определения величин моментов по сечениям строим график-эпюру крутящих моментов вдоль оси бруса.

Крутящий момент считаем положительным, если моменты внешних пар сил направлены по часовой стрелке, в этом случае мо­мент внутренних сил упругости направлен против часовой стрелки (рис. 26.2).

                             

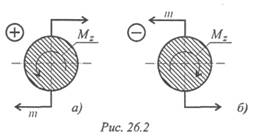
Порядок построения эпюры моментов аналоги­чен построению эпюр про­дольных сил. Ось эпюры параллельна оси бруса, значения моментов откла­дывают от оси вверх или вниз, масштаб построе­ния выдерживать обязательно.

      Примеры решения задач

Пример 1. На распределительном валу (рис. 26.3) установлены четыре шкива,  на   вал   через   шкив   1  подается  мощность  12 кВт,  кото­рая  через шкивы 2, 3, 4  передается  потребителю;  мощности распре­деляются   следующим   образом:   Р2 =  8 кВт ,   Рз  =  3 кВт ,    Р4  =  1кВт ,

               Тема 2.5. Кручение. Внутренние силовые факторы при кручении                      219

 

вал вращается с постоянной скоростью ώ = 25 рад/с. Построить эпюру крутящих моментов на валу.

                

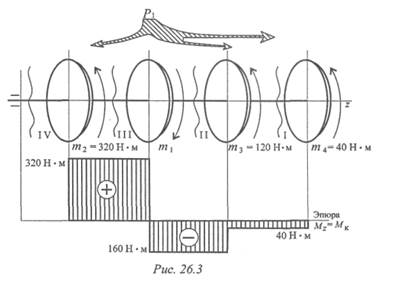
Решение

1. Определяем моменты пар сил на шкивах. Вращающий момент определяем из формулы мощности при вра­щательном движении

                                               

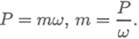
Момент на шкиве1 движущий, а моменты на шкивах 2, 3, 4 — моменты сопротивления механизмов, поэтому они имеют противо­положное направление. Брус скручивается между движущим момен­том и моментами сопротивления. При равновесии момент движущий равен сумме моментов сопротивления:

 

        

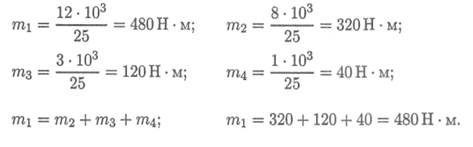
220                                                                                    Лекция 26

2. Определяем крутящие моменты в поперечных сечениях бруса
с помощью метода сечений.

      

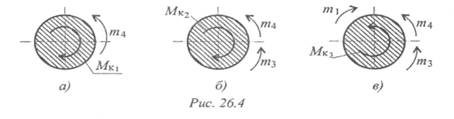
Сечение I (рис. 26.4а):

- m4 + М_К1 = 0; М_К1 = m4; М_{К 1} = 40Н • м — крутящий момент отрицательный.

Сечение II (рис. 26.4b):

- m4 – т ₃ + М_К2 = 0; М_К2 = m4 + m3; М_К2 = 40 + 120 = 160Н•м — крутящий момент отрицательный.

Сечение III (рис. 26.4в):

- m4 – т ₃ + т 1 — М_кз = 0; -М_кз = m4 + т ₃ - т 1;

-М_кз = 40 + 120 - 480; М_Кз = 320 Н • м — крутящий момент поло­жительный.

Сечение IV :

M_{K 4} = - m4 – т ₃ + т 1   – т ₂= 0.

3. Строим эпюру крутящих моментов. Заметим, что скачок на
эпюре всегда численно равен приложенному вращающему моменту.

Выбираем соответствующий масштаб.

Откладываем значения моментов, штрихуем эпюру поперек, об­водим по контуру, записываем значения моментов (см. эпюру под схемой вала (рис. 26.3)). Максимальный крутящий момент на участ­ке III Мкз =320Н•м.

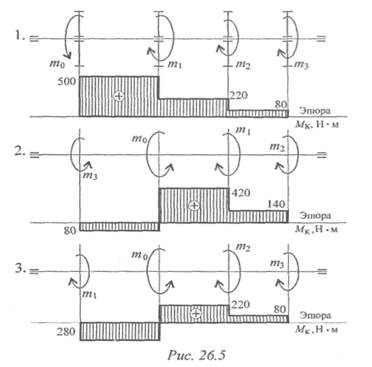
Пример 2.  Выбрать рациональное расположение колес на валу (рис. 26.5). т 1= 280 Н • м; т₂ = 140 Н • м; т₃ = 80 Н • м.

Примечание. Меняя местами колеса (шкивы) на валу, можно изменять величины крутящих моментов. Рациональным рас­положением является такое, при котором крутящие моменты принимают минимальные из возможных значения.

        m0 = т ₁ + т 2   + т ₃ = 280 + 140 + 80 = 500 Н • M.

                Тема 2.5. Кручение. Внутренние силовые факторы при кручении                      221

 

Рассмотрим нагрузки на валу при различном расположении колес.

Из представленных вариантов наиболее рационально располо­жение шкивов в третьем случае, здесь значения крутящих момен­тов минимальны. Вывод: при установке шкивов желательно, чтобы мощность подавалась в середине вала и по возможности равномерно распределялась направо и налево.

 

    

 

     Контрольные  вопросы и задания

1. Какие деформации возникают при кручении?

2. Какие гипотезы выполняются при деформации кручения?

3. Изменяются ли длина и диаметр вала после скручивания?

222                                                                                          Лекция 26

4. Какие внутренние силовые факторы возникают при кручении?

5. Что такое рациональное расположение колес на валу?

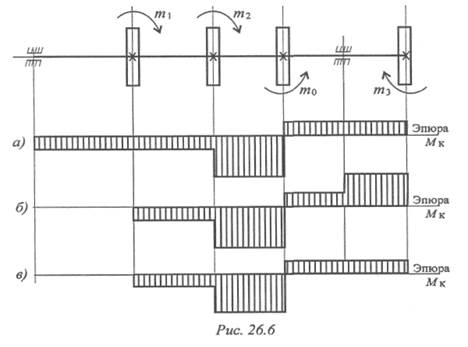
6. Для заданного вала (рис. 26.6) выбрать соответствующую
эпюру крутящих моментов (а, б, в). m 1 = 40Н•м; т 2 = 180Н•м;
m₀ = 280Н•м.

  

 

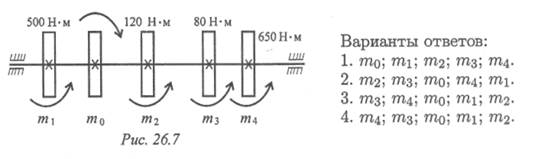
7. В каком порядке рациональнее расположить шкивы на валу
для уменьшения нагрузки на вал (рис. 26.7)?

 

     

                                                                                        Тема 2.5. Кручение                                                                                        223

ЛЕКЦИЯ 27

Тема 2.5. Кручение.

Напряжения и деформации

При кручении

Иметь представление о напряжении и деформациях при круче­нии, о моменте сопротивления при кручении.

Знать формулы для расчета напряжений в точке поперечного сечения, закон Гука при кручении.

Напряжения при кручении

Проводим на поверхности бру­са сетку из продольных и попе­речных линий и рассмотрим рису­нок, образовавшийся на поверхно­сти после деформации (рис. 27.1а). Поперечные окружности, оставаясь плоскими, поворачиваются на угол φ , продольные линии искривляют­ся, прямоугольники превращают­ся в параллелограммы. Рассмотрим элемент бруса 1234 после деформа­ции.

                                   

                     

При  выводе    формул    используем    закон    Гука    при    сдвиге    и    гипотезу

224                                                                       Лекция 27

плоских сечений и неискривления радиусов поперечных сечений.

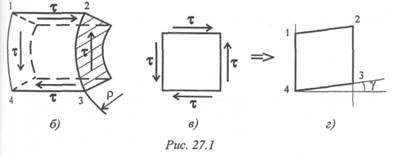
При кручении возникает напряженное состояние, называемое «чистый сдвиг» (рис. 27.16).

При сдвиге на боковой поверхности элемента 1234 возникают касательные напряжения, равные по величине (рис. 27.1в), элемент деформируется (рис. 27.1г).

Материал подчиняется закону Гука. Касательное напряжение пропорционально углу сдвига.

Закон Гука при сдвиге τ = Gγ ,

G — модуль упругости при сдвиге, Н/мм²; γ -- угол сдвига, рад.

              Напряжение в любой точке поперечного сечения

   Рассмотрим поперечное сечение круглого бруса. Под действием внешнего момента в каждой точке поперечного сечения возникают силы упругости dQ (рис. 27.2).

                                            

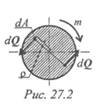
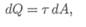
 где τ — касательное напряжение; dA — элементарная площадка.

  В силу симметрии сечения силы dQ образуют пары (см. лекцию 26).

Элементарный момент силы dQ относительно центра круга

       

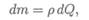
где р — расстояние от точки до центра круга.

Суммарный момент сил упругости получаем сложением (интегрированием) элементарных моментов:

         

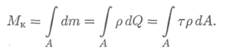
После преобразования получим формулу для определения напря­жений в точке поперечного сечения:

         

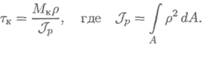
            Тема 2.5. Кручение                                                   225

При ρ = 0 τ_к = 0; касательное напряжение при кручении про­порционально расстоянию от точки до центра сечения. Полученный интеграл J_p (лекция 25) называется полярным моментом инерции сечения. J_p является геометрической характеристикой сечения при кручении. Она характеризует сопротивление сечения скручиванию.

Анализ полученной формулы для J_p показывает, что слои, рас­положенные дальше от центра, испытывают большие напряжения.

Эпюра распределения касательных напряжений при кручении (рис. 27.3)

   

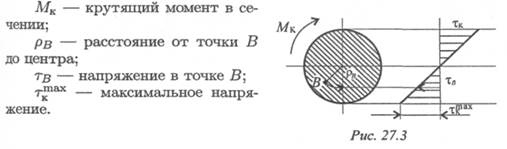
      Максимальные   напряжения   при   кручении

Из формулы для определения напряжений и эпюры распределе­ния касательных напряжений при кручении видно, что максималь­ные напряжения возникают на поверхности.

Определим максимальное напряжение, учитывая, что р_{т a х} = d /2, где d — диаметр бруса круглого сечения.

Для круглого сечения полярный момент инерции рассчитыва­ется по формуле (см. лекцию 25).

             

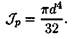
Максимальное напряжение возникает на поверхности, поэтому имеем 

                                            

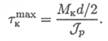
Обычно Jp / р_{т a х} обозначают W_p и называют моментом сопро­тивления при кручении, или полярным моментом сопротивления сечения

8 - 8060 Олофинская

226                                                                                  Лекция 27

Таким образом, для расчета максимального напряжения на по­верхности круглого бруса получаем формулу

           

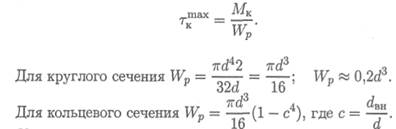
Условие прочности при кручении

Разрушение бруса при кручении происходит с поверхности, при расчете на прочность используют условие прочности

             

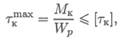
где [τ_к] — допускаемое напряжение кручения.

                                    

                                    Виды  расчетов  на  прочность

Существует два вида расчета на прочность

1. Проектировочный расчет — определяется диаметр бруса
(вала) в опасном сечении:

      

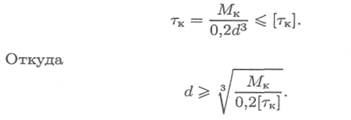
2. Проверочный расчет — проверяется выполнение условия прочности  

                                                  

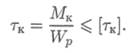
3. Определение нагрузочной способности (максимального крутящего момента)

                                                        

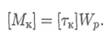
                                                                 Тема 2.5. Кручение                                                             227

Расчет на жесткость

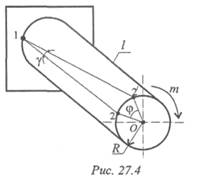
При расчете на жесткость определяется деформация и сравни­вается с допускаемой. Рассмотрим деформацию круглого бруса над действием внешней пары сил с моментом т (рис. 27.4).

При кручении деформация оце­нивается углом закручивания:

                                      

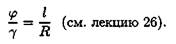
Здесь φ — угол закручивания; γ — угол сдвига; l — длина бруса; R — радиус; R = d /2. Откуда

             

                                                

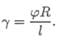
Закон Гука имеет вид τ_к = Gγ .

Подставим выражение для γ получим

           

oткуда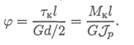                                            

Произведение GJ_P называют жесткостью сечения.

Модуль упругости можно определить как G = 0,4Е. Для стали G = 0,8·10⁵МПа.

Обычно рассчитывается угол закручивания, приходящийся на один метр длины бруса (вала) φ0.

Условие жесткости при кручении можно записать в виде

             

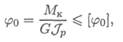
где φ0 — относительный угол закручивания, φ0 = φ/ l ;

[φ0] ≈1град/м = 0,02рад/м — допускаемый относительный угол закручивания.

228                                                                    Лекция 27

Примеры решения задач

Из расчетов на прочность и жесткость определить потреб­ный диаметр вала для передачи мощности 63 кВт при скорости 30 рад/с. Материал вала — сталь, допускаемое напряжение при кручении 30 МПа; допускаемый относительный угол закручивания [φ0] = 0,02 рад/м; модуль упругости при сдвиге G = 0,8 • 10⁵ МПа.

                                                        Решение

1. Определение размеров поперечного сечения из расчета на
прочность.

Условие прочности при кручении:

            

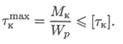
Определяем вращающий момент из формулы мощности при вра­щении:

                

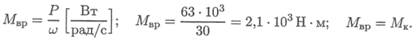
Из условия прочности определяем момент сопротивления вала при кручении 

                                             

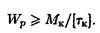
Значения подставляем в ньютонах и мм.

                  

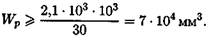
Определяем диаметр вала:

                   

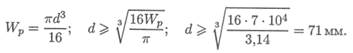
2. Определение размеров поперечного сечения из расчета на
жесткость.

Условие жесткости при кручении:

            

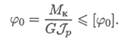
                                                                  Тема 2.5. Кручение                                                          229

Из условия жесткости определяем момент инерции сечения при кручении:

                 

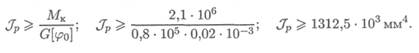
Определяем диаметр вала:

                 

3. Выбор потребного диаметра вала из расчетов на прочность и жесткость.

Для обеспечения прочности и жесткости одновременно из двух найденных значений выбираем большее.

Полученное значение следует округлить, используя ряд пред­почтительных чисел. Практически округляем полученное значение так, чтобы число заканчивалось на 5 или 0. Принимаем значение

dвала = 75 ММ.

Для определения диаметра вала желательно пользоваться стан­дартным рядом диаметров, приведенном в Приложении 2.

        

          Контрольные вопросы и задания

1. Как называется напряженное состояние, возникающее при кручении круглого бруса (вала)?

2. Напишите закон Гука при сдвиге.

3. Чему равен модуль упругости материала при кручении для стали? В каких единицах он измеряется?

4. Какая связь между углом сдвига и углом закручивания?

5. Как распределяется касательное напряжение при кручении? Чему равно напряжение в центре круглого поперечного сечения?

6. Напишите формулу для расчета напряжения в любой точке поперечного сечения.

7. Что такое полярный момент инерции? Какой физический
смысл имеет эта величина? В каких единицах измеряется?

Напишите формулу для расчета полярного момента инерции для круга.

230                                                                       Лекция 27

8. Напишите формулу для расчета напряжения на поверхности вала при кручении. Как изменится напряжение, если диаметр вала увеличится в два раза?

9. Почему для деталей, работающих на кручение, выбирают круглое поперечное сечение?

10. В чем заключается расчет на прочность?

11. В чем заключается расчет на жесткость?

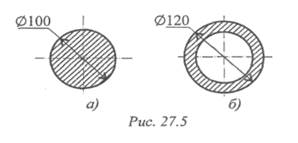
12. По величине допускаемых крутящих моментов сравнить не­сущую способность двух валов из одинакового материала, имею­щих примерно одинаковую площадь поперечных сечений с = 0,55 (рис. 27.5). Сравнение провести по формуле [М_к] = [ τ ĸ ]  W_p.

       

13. Ответьте на вопросы тестового задания.

Тема 2.5. Кручение

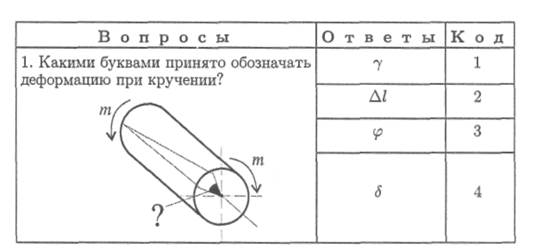
         Тема 2.5. Кручение                                                    231

 

232                                                                    Лекция 28

ЛЕКЦИЯ 28

Тема 2.5. Кручение.