При кручении

Иметь представление о рациональных формах поперечного се­ чения и рациональном расположении колес на валу.

Знать условия прочности и жесткости при кручении.

Уметь выполнять проектировочные и проверочные расчеты круглого бруса для статически определимых систем.

Примеры решения задач

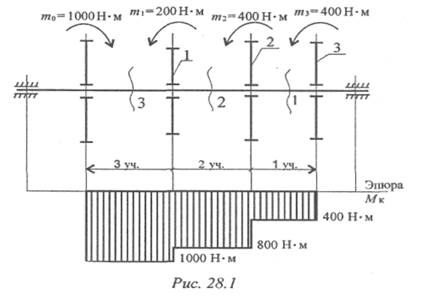
Пример 1. Для заданного бруса (рис. 28.1) построить эпюры крутящих моментов, рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента. Построить эпюру крутящих моментов при рациональном располо­жении шкивов.

Из    условия    прочности    определить диаметры    вала    для    сплошного

                                  Тема 2.5. Кручение                                                    233

и кольцевого сечений, приняв 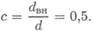  Сравнить полученные результаты по полученным площадям поперечных сечений. [τ_к] = 35МПа.

           Решение

1. Пользуясь методом сечений, определяем крутящие моменты на участках вала (рис. 28.2).

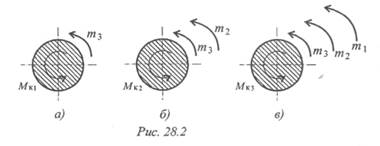
Сечение 1 (рис. 28.2а): M_K1 = mз = 400 Н·м.

Сечение 2 (рис. 28.26): М_к2 = m₃ + m2 = 800 Н·м.

Сечение 3 (рис. 28.2в): М_кз = т 3 + т 2 + m 1 = 1000 Н·м.

2. Строим эпюру крутящих моментов. Значения крутящих моментов откладываем вниз от оси, т. к. моменты отрицательные.

Максимальное значение крутящего момента на валу в этом слу­чае 1000Н·м (рис. 28.1).

3. Выберем рациональное расположение колес на валу. Наибо­лее целесообразно такое размещение колес, при котором наибольшие положительные и отрицательные значения крутящих моментов на участках будут по воз­можности одинаковыми.
Из этих соображений ве­дущий шкив, передающий момент 1000 Н·м, помещаем ближе к центру вала, ведомые шкивы 1 и 2 раз­мещаем слева от ведущего
с  моментом    1000 Н·м ,    шкив 3    остается    на    том    же    месте .

234                                                                     Лекция 28

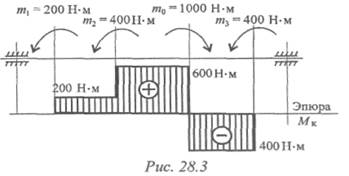
Строим эпюру крутящих моментов при выбранном расположении шкива (рис. 28.3).

Максимальное значение крутящего момента на валу при вы­бранном расположении колес на валу 600 Н·м.

4. Определяем диаметры вала по сечениям при условии, что сечение — круг.

Условие прочности при кручении τ_к = M_K / W_P ≤ [τ_к]. Момент сопротивления кручению

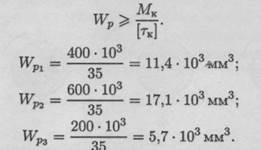
Определяем диаметры вала по сечениям:

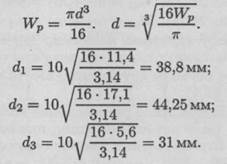
Округляем полученные значения: d1 = 40 мм; d2= 45 мм; d 3 = 35 мм.

5. Определяем диаметры вала по сечениям при условии, что се­чение — кольцо.

Моменты сопротивления остаются теми же.

По условию с = d _BH / d = 0,5.

Полярный момент сопротивления кольца

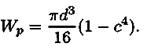
               Тема 2.5. Кручение                                                 235

Формула для определения наружного диаметра вала кольцевого сечения будет следующей:

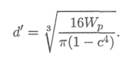
Расчет можно провести по формуле

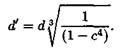
Диаметры вала по сечениям:

Наружные диаметры вала кольцевого сечения практически не изменились.

Для кольцевого сечения: d '₁ = 40 мм; d '₂ = 46 мм; d '₃ = 35 мм.

6. Для вывода об экономии металла при переходе на кольцевое сечение сравним площади сечений (рис. 28.4).

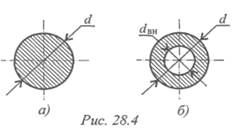
При условии, что сечение — круг (рис. 28.4а):

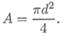
Сплошное круглое сечение: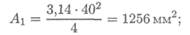

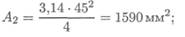
236                                                               Лекция 28

Следовательно, при переходе с кругового на кольцевое сечение экономия металла по весу составит 1,3 раза.

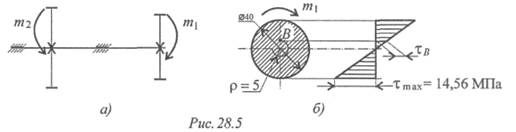
Пример 2. Стальной вал диаметром 40 мм передает мощность 15 кВт при угловой скорости 80 рад/с (рис. 28.5); проверить проч­ность и жесткость вала, если допускаемое напряжение кручения 20МПа. Модуль упругости при сдвиге 0,8 • 10⁵МПа. Допускаемый угол закручивания [φ о ] = 0,бград/м. Построить эпюру касательных напряжений и определить значение касательного напряжения в точ­ке, удаленной на 5 мм от оси вала.

                                                  Тема 2.5. Кручение                                                   237

       Решение

1. Определяем вращающий момент на валу:

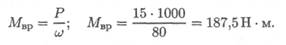
2. Проверка прочности вала.

Из условия равновесия m 1 + m 2 = 0; m 1 = m 2 = М_к.

Условие прочности: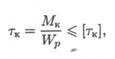        

где τ_к — расчетное напряжение в сечении; М_к — крутящий момент в сечении; W_p — момент сопротивления; [τ_к] — допускаемое напря­жение кручения.

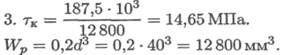
4. Прочность обеспечена. Максимальное касательное напряже­ние в сечении 14,65 МПа < 20 МПа.

5. Проверка жесткости.
Условие жесткости:

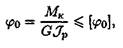
где φ o — относительный угол закручивания; J_p — полярный момент инерции при кручении; [φ o] — допускаемый угол закручивания.

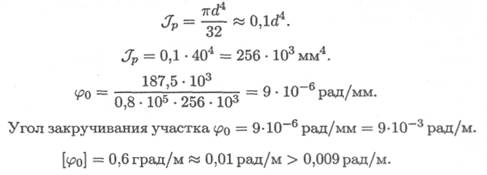
238                                                                                  Лекция 28

Жесткость обеспечена.

6. Построим эпюру касательных напряжений в поперечном сече­нии (рис. 28.5b). Определим напряжение в точке, удаленной на 5 мм от оси вала.

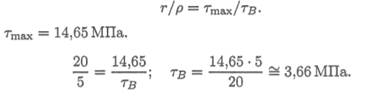
        Контрольные вопросы и задания

1. Определите крутящий момент в сечении 2-2 (рис. 28.6).

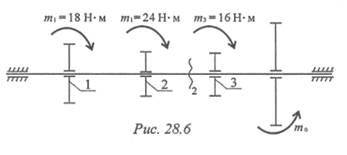
2. В каком порядке рациональнее расположить шкивы, что­бы получить минимальную нагрузку на вал? Использовать схему рис. 28.6.

3. Как изменится напряжение в сечении, если диаметр вала уменьшить в два раза?

4. Проведены расчеты вала на прочность и жесткость. Получе­но: диаметр вала из расчета на прочность 65 мм, диаметр вала из расчета на жесткость 70 мм. Каким должен быть вал?

5. Как изменится угол закручивания вала, если крутящий мо­мент увеличить в 4 раза, а диаметр уменьшить в 2 раза?

6. Напишите условия прочности и жесткости при кручении.

              Тема 2.6. Изгиб. Классификация видов изгиба                                              239

ЛЕКЦИЯ 29

                   Тема 2.6. Изгиб.

       Классификация видов изгиба.