A – некоторое множество физических объектов, цен, услуг и т. д.;
N – множество натуральных чисел N= {1, 2, 3,... };
Z – множество целых чисел Z= {0, ±1, ±2, ±3,... };
Q – множество рациональных чисел Q= {  :
: 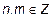 ,
, 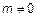 };
};
R – множество действительных (вещественных) чисел.
Множество может содержать много элементов или лишь несколько, например множество русских букв содержит ровно 33 элемента. Множество натуральных чисел N содержит бесконечно много элементов. Может быть и предельный случай, когда множество вообще не содержит элементов, например множество действительных корней уравнения x4+8 = 0.
Определение 2.
Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается 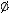 .
.
В общем случае множества бывают конечные и бесконечные.
|
Конечное множество – это такое множество, для которого существует натуральное число, равное числу его элементов.
Например, множество русских букв – конечное множество, так как существует натуральное число 33, равное числу элементов этого множества.
Определение 4.
Множество, не являющееся конечным, называется бесконечным множеством.
Замечание!!!
Перечислением можно задать только конечные множества. Вторым и третьим способами задаются бесконечные множества.
Уже рассмотренное нами множество натуральных чисел N – бесконечное множество, поскольку нет такого натурального числа, которое равнялось бы числу его элементов.
Определение 5.
Если множество A – конечное множество, то через |A| обозначают число его элементов и называют мощностью множества A. Понятие мощности вводится и для бесконечных множеств.
ПРИМЕР 4.
Пусть множество A состоит из элементов {январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь} – это множество месяцев одного года. Мощность |A| заданного таким образом множества A равна 12. Это число элементов множества A – количество месяцев одного года.
Определение 6.
Два конечных множества A и B называются равными, если они состоят из одних и тех же элементов. Если множества A и B равны, то мы будем писать A = B, в противном случае A 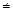 B.
B.
Вывод!!!
В равных множествах последовательность элементов не важна. Таким образом, мы получили следующее определение:
Определение 7.
Два конечных множества A и B не равны между собой, если в множестве A есть элемент, не принадлежащий множеству B или наоборот.
Вывод!!!
Согласно такому определению равенства множеств мы, естественно, получаем, что все пустые множества равны между собой или (что то же самое) что существует только одно пустое множество 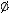 .
.
ПРИМЕР 5.
1. Множества {0, 1, 2}={1, 2, 0} равны между собой и поэтому между ними мы можем поставить знак равенства: они конечны и состоят из одних и тех же элементов.
|
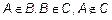 .
.
Важно!!!
Дата: 2018-12-21, просмотров: 379.