Активная мощность трехфазной системы определяется как сумма активных мощностей фаз нагрузки с учетом активной мощности в сопротивлении нулевого провода:
P=PA+PB+PC+P0.
Реактивная мощность трехфазной системы определяется аналогично:
Q=QA+QB+QC+Q0.
Полная мощность несимметричной трехфазной нагрузки равна
.
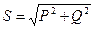В симметричной трехфазной системе активную, реактивную и полную мощности можно найти следующим образом:
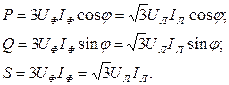
В уравновешенных системах суммарная активная мощность постоянна и не зависит от времени: P=PA+PB+PC=3UфIфcos j =P.
В несимметричной трехфазной системе полная, активная и реактивная мощности определяется отдельно для каждой фазы нагрузки:
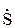A = 
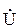АН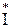 
A = PA + jQA = UAHIA cosjA + jUAHIA sinj;
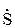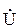B = ВН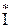 
B = PB + jQB = UBHIB cosjB + jUBHIB sinj;
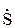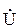C = СН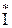 
C = PC + jQC = UCHIC cosjC + jUCHIC sinj;
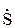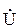0 = 00’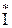 
0 = P0 + jQ0 = U00’I0 cosj0 + jU00’I0 sinj.
Задание 1. Расчет простых цепей постоянного тока
Задание: Схема, составленная из резистивных элементов, питается от источника постоянного напряжения (источник подключен ко входным зажимам «а» и «b», причем положительный полюс источника соединен с зажимом «а»). Рассчитать токи во всех ветвях схемы и падения напряжений на каждом из резисторов. Вариант схемы каждому студенту принять в соответствии с его порядковым номером в списке группы. Параметры элементов схем для каждого варианта приведены в таблице 4.1.
Таблица 4.1
Варианты задания и параметры элементов схем
| Вари-ант | Схема (№ рис.) | Значения сопротивлений резисторов, Ом | Напряжение источника, В | |||
| R1 | R2 | R3 | R4 | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 4.1 | 1 | 10 | 6 | 4 | 10 |
| 2 | 4.2 | 2 | 5 | 10 | 8 | 15 |
| 3 | 4.3 | 10 | 7 | 4 | 2 | 20 |
| 4 | 4.4 | 5 | 9 | 2 | 3 | 25 |
| 5 | 4.5 | 6 | 5 | 2 | 4 | 30 |
| 6 | 4.6 | 2 | 3 | 5 | 10 | 10 |
| 7 | 4.7 | 3 | 7 | 6 | 4 | 15 |
| 8 | 4.8 | 3 | 2 | 1 | 4 | 20 |
| 9 | 4.9 | 1 | 3 | 5 | 10 | 25 |
| 10 | 4.10 | 2 | 8 | 3 | 1 | 30 |
| 11 | 4.11 | 4 | 2 | 8 | 1 | 10 |
| 12 | 4.12 | 2 | 4 | 1 | 5 | 15 |
| 13 | 4.13 | 3 | 8 | 2 | 2 | 20 |
| 14 | 4.14 | 8 | 3 | 5 | 7 | 25 |
| 15 | 4.15 | 5 | 5 | 2 | 3 | 30 |
| 16 | 4.16 | 7 | 3 | 10 | 5 | 10 |
| 17 | 4.17 | 4 | 5 | 2 | 2 | 15 |
| 18 | 4.18 | 5 | 3 | 3 | 10 | 20 |
| 19 | 4.19 | 5 | 2 | 2 | 1 | 25 |
| 20 | 4.20 | 2 | 5 | 7 | 3 | 30 |
| 21 | 4.21 | 7 | 5 | 4 | 3 | 10 |
| 22 | 4.22 | 5 | 3 | 6 | 7 | 15 |
| 23 | 4.23 | 9 | 3 | 5 | 1 | 20 |
| 24 | 4.24 | 7 | 3 | 5 | 5 | 25 |
| 25 | 4.25 | 3 | 5 | 2 | 8 | 30 |
| 26 | 4.1 | 2 | 5 | 3 | 8 | 10 |
| 27 | 4.2 | 1 | 4 | 2 | 3 | 15 |
| 28 | 4.3 | 5 | 6 | 10 | 3 | 20 |
| 29 | 4.4 | 8 | 7 | 4 | 2 | 25 |
| 30 | 4.5 | 3 | 2 | 4 | 6 | 30 |
| 31 | 4.6 | 5 | 9 | 7 | 4 | 10 |
| 32 | 4.7 | 5 | 4 | 6 | 1 | 15 |
| 33 | 4.8 | 6 | 8 | 3 | 5 | 20 |
| 34 | 4.9 | 9 | 1 | 3 | 4 | 25 |
| 35 | 4.10 | 4 | 6 | 5 | 3 | 30 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 36 | 4.11 | 1 | 7 | 2 | 4 | 10 |
| 37 | 4.12 | 4 | 8 | 3 | 7 | 15 |
| 38 | 4.13 | 6 | 4 | 5 | 5 | 20 |
| 39 | 4.14 | 3 | 6 | 9 | 10 | 25 |
| 40 | 4.15 | 7 | 3 | 8 | 1 | 30 |
| 41 | 4.16 | 4 | 9 | 2 | 3 | 10 |
| 42 | 4.17 | 9 | 1 | 2 | 5 | 15 |
| 43 | 4.18 | 8 | 2 | 5 | 6 | 20 |
| 44 | 4.19 | 6 | 5 | 7 | 3 | 25 |
| 45 | 4.20 | 3 | 8 | 6 | 4 | 30 |
| 46 | 4.21 | 5 | 7 | 2 | 9 | 10 |
| 47 | 4.22 | 8 | 10 | 7 | 6 | 15 |
| 48 | 4.23 | 5 | 4 | 1 | 3 | 20 |
| 49 | 4.24 | 6 | 5 | 7 | 9 | 25 |
| 50 | 4.25 | 5 | 1 | 3 | 7 | 30 |
При выполнении задания студенту следует вычертить схему в соответствии с заданным вариантом и выписать исходные данные (значения напряжения источника Uab, сопротивлений R 1¸R 4). Затем необходимо проанализировать схему, определив виды соединения резисторов на отдельных участках схемы (последовательное или параллельное), после чего, постепенно «сворачивая» схему (заменяя последовательное или параллельное соединение резисторов на отдельных участках эквивалентными сопротивлениями), найти эквивалентное сопротивление всей цепи R Э относительно входных зажимов «а» и «b». После этого следует определить значение тока в неразветвленной части цепи, а затем, постепенно «разворачивая» схему, найти токи в отдельных ветвях схемы и напряжения на каждом из резисторов.
Варианты схем для выполнения задания 1
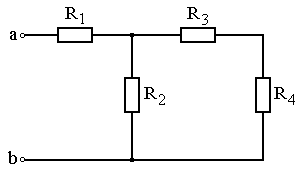
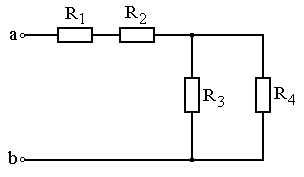
Рис. 4.1 Рис. 4.2
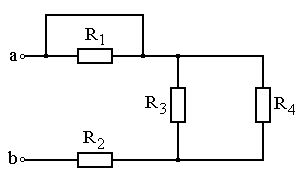
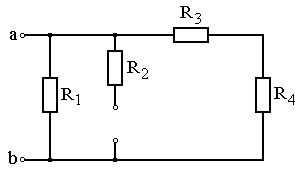
Рис. 4.3 Рис. 4.4
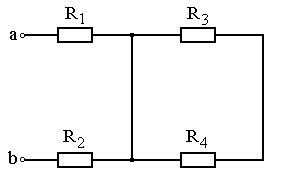
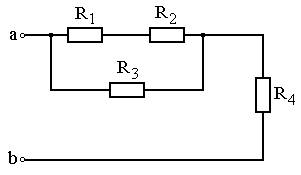
Рис. 4.5 Рис. 4.6
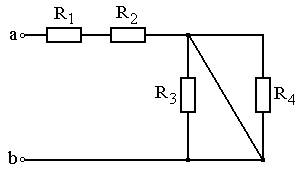
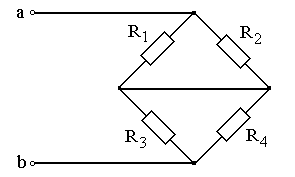
Рис. 4.7 Рис. 4.8
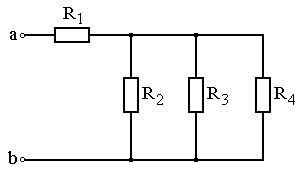
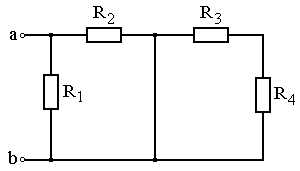
Рис. 4.9 Рис. 4.10
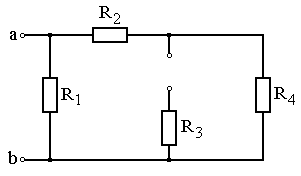
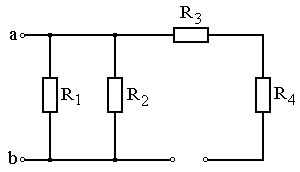
Рис. 4.11 Рис. 4.12
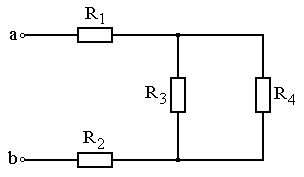
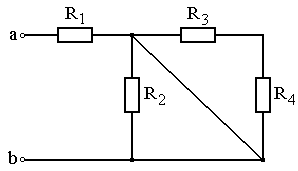
Рис. 4.13 Рис. 4.14
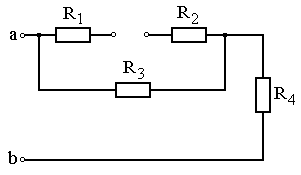
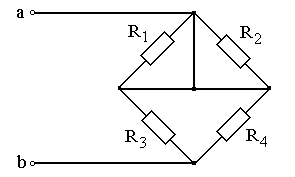
Рис. 4.15 Рис. 4.16
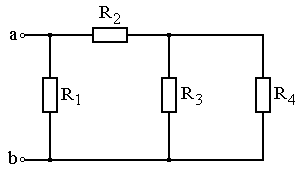
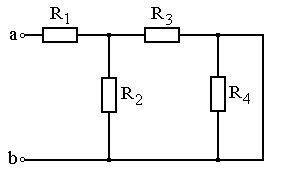
Рис. 4.17 Рис. 4.18
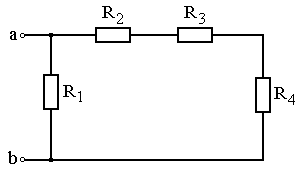
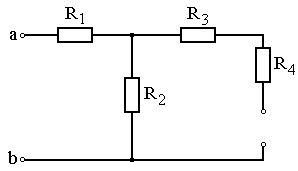
Рис. 4.19 Рис. 4.20
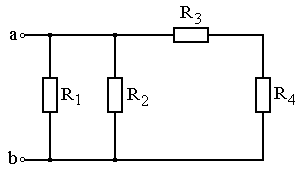
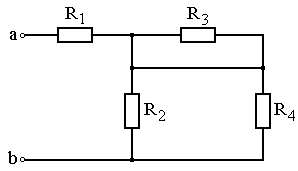
Рис. 4.21 Рис. 4.22
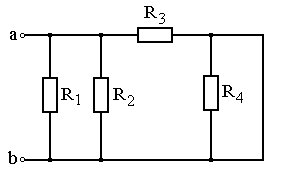
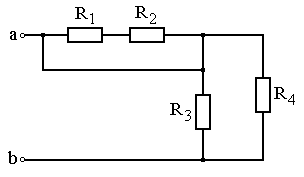
Рис. 4.23 Рис. 4.24
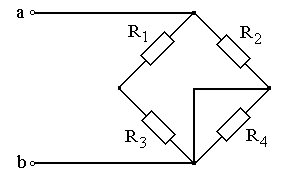
Рис. 4.25
Пример расчета простой цепи постоянного тока.
В схеме, изображенной на рис. 4.26, напряжение источника Uab=20 В, сопротивления резисторов равны соответственно: R 1=5 Ом, R 2=3 Ом, R 3=2 Ом, R 4=4 Ом, R 5=7 Ом. Рассчитать токи во всех ветвях схемы и падения напряжений на каждом из резисторов.
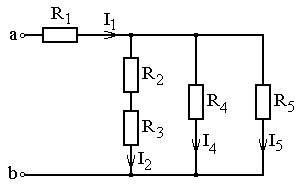
Рис. 4.26. Исходная схема для расчета
Очевидно, что резисторы R 2 и R 3 соединены последовательно, поэтому общее сопротивление данной ветви (рис. 4.27, а) можно найти как
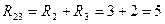Ом.
Резисторы R 4 и R 5 соединены параллельно, поэтому эквивалентное сопротивление двух этих ветвей (рис. 4.27, а) можно найти как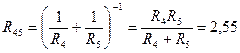 
Ом.
В свою очередь, сопротивления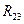 
и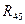 
между собой соединены параллельно, поэтому их можно заменить сопротивлением 
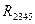(рис. 4.27, б): 
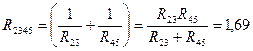Ом.
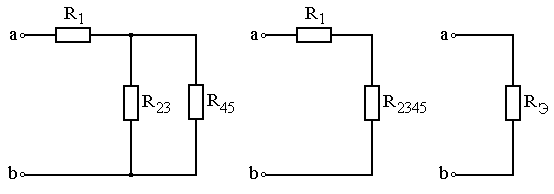
а б в
Рис. 4.27. Последовательность отыскания эквивалентного сопротивления
Величину эквивалентного сопротивления R Э всей схемы (рис. 4.27, в) находим как сумму R 2345 и R 1, так как данные сопротивления соединены последовательно; R Э=R 1+R 2345=6,69 Ом.
Ток I1 в неразветвленной части цепи может быть найден как
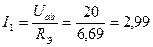А.
Для нахождения остальных токов необходимо знать напряжение на резисторах R 4, R 5 и R 23. Эти резисторы соединены параллельно, поэтому напряжение на них одинаково и равно напряжению на сопротивлении R 2345, которое может быть найдено как
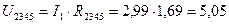В.
Токи в параллельных ветвях исходной схемы равны:
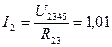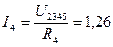А,
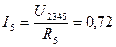А,
А.
Проверку полученных результатов можно провести по первому закону Кирхгофа, в соответствии с которым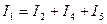 
. Подстановка чисел в данное выражение дает 2,99 А = 2,99 А. Токи определены верно.
Напряжения на резисторах исходной схемы равны:
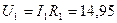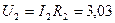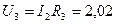В,
В,
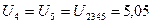В,
В.
Задание 2. Расчет сложных цепей постоянного тока
Задание: для электрических схем (варианты параметров элементов схем и номера схем для расчета каждым из методов приведены в таблицах 5.1 и 5.2) выполнить следующее:
1. Определить величины и направления токов во всех ветвях схемы по методу уравнений Кирхгофа.
1.1. Вычертить заданную схему, выписать заданные величины э.д.с. и сопротивлений;
1.2. Задать произвольные положительные направления токов в ветвях схемы (индексы токов при этом должны совпадать с индексами сопротивлений в соответствующих ветвях), определить число независимых узлов схемы, определить число независимых контуров схемы и задаться направлениями их обхода;
1.3. Составить необходимое количество уравнений по первому и второму законам Кирхгофа; полученную систему уравнений решить относительно неизвестных токов, определив их величину и истинное направление;
1.4. Произвести проверку правильности расчета токов путем составления уравнения баланса мощностей цепи.
2. Определить величины и направления токов во всех ветвях схемы по методу контурных токов.
2.1. Вычертить заданную схему, выписать заданные величины э.д.с. и сопротивлений;
2.2. Выбрать независимые контуры, задаться в них произвольными направлениями контурных токов;
2.3. Составить систему уравнений для контурных токов по второму закону Кирхгофа; решить данную систему относительно неизвестных контурных токов;
2.4. Определить значения токов в ветвях схемы через найденные контурные токи;
2.5. Произвести проверку правильности расчета токов путем составления уравнения баланса мощностей цепи.
3. Определить величины и направления токов во всех ветвях схемы по методу наложения.
3.1. Вычертить заданную схему, выписать заданные величины э.д.с. и сопротивлений;
3.2. Составить частичные схемы замещения исходной схемы; для каждой из частичных схем замещения задать направления токов в ветвях и определить эти токи, пользуясь законами Ома и Кирхгофа. По найденным токам частичных схем замещения найти полные токи в ветвях исходной схемы;
3.4. Проанализировать режимы работы источников э.д.с.;
3.5. Произвести проверку правильности расчета токов путем составления уравнения баланса мощностей цепи.
Таблица 5.1.
Параметры элементов схем для расчета
| Схема (№ рисунка) | Вариант параметров | Параметры элементов схемы | ||||||
| Е1, В | Е2, В | R1 , Ом | R 2 , Ом | R 3 , Ом | R 4 , Ом | R 5 , Ом | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 5.1 | 1 | 20 | 25 | 5 | 5 | 10 | 15 | 10 |
| 5.1 | 2 | 30 | 20 | 10 | 5 | 5 | 10 | 10 |
| 5.2 | 1 | 30 | 20 | - | 10 | 15 | 10 | 5 |
| 5.2 | 2 | 15 | 25 | - | 5 | 10 | 15 | 15 |
| 5.3 | 1 | 35 | 40 | 10 | 10 | 15 | 5 | 10 |
| 5.3 | 2 | 20 | 35 | 10 | 15 | 10 | 10 | 5 |
| 5.4 | 1 | 45 | 25 | 15 | 5 | 10 | 10 | 5 |
| 5.4 | 2 | 35 | 15 | 10 | 15 | 5 | 15 | 15 |
| 5.5 | 1 | 15 | 25 | 15 | 10 | 5 | 5 | 5 |
| 5.5 | 2 | 40 | 30 | 15 | 15 | 10 | 10 | 15 |
| 5.6 | 1 | 20 | 30 | 5 | - | 10 | 10 | 15 |
| 5.6 | 2 | 20 | 15 | 10 | - | 5 | 5 | 10 |
| 5.7 | 1 | 25 | 30 | 10 | 10 | 5 | 15 | 5 |
| 5.7 | 2 | 35 | 25 | 5 | 5 | 10 | 15 | 10 |
| 5.8 | 1 | 30 | 35 | 15 | 10 | 10 | 15 | 10 |
| 5.8 | 2 | 45 | 35 | 10 | 10 | 15 | 15 | 10 |
| 5.9 | 1 | 35 | 20 | 10 | 15 | 5 | 10 | 15 |
| 5.9 | 2 | 15 | 20 | 15 | 5 | 5 | 10 | 15 |
| 5.10 | 1 | 40 | 25 | 15 | 5 | 10 | 15 | 10 |
| 5.10 | 2 | 25 | 30 | 10 | 10 | 5 | 5 | 10 |
| 5.11 | 1 | 30 | 20 | 5 | 15 | 15 | 10 | 10 |
| 5.11 | 2 | 35 | 15 | 15 | 5 | 10 | 10 | 5 |
| 5.12 | 1 | 15 | 25 | 10 | 15 | 5 | 10 | 5 |
| 5.12 | 2 | 20 | 15 | 5 | 15 | 10 | 10 | 10 |
| 5.13 | 1 | 35 | 25 | 5 | 10 | 15 | 10 | 10 |
| 5.13 | 2 | 20 | 25 | 10 | 5 | 15 | 15 | 5 |
| 5.14 | 1 | 20 | 40 | 5 | - | 10 | 15 | 15 |
| 5.14 | 2 | 30 | 15 | 10 | - | 5 | 5 | 10 |
| 5.15 | 1 | 25 | 40 | 10 | - | 15 | 10 | 10 |
| 5.15 | 2 | 35 | 20 | 5 | - | 15 | 5 | 10 |
| 5.16 | 1 | 30 | 25 | 10 | 10 | 15 | 5 | 5 |
| 5.16 | 2 | 40 | 30 | 5 | 15 | 15 | 10 | 10 |
| 5.17 | 1 | 15 | 25 | 15 | 10 | 15 | 5 | 10 |
| 5.17 | 2 | 45 | 20 | 10 | 15 | 10 | 10 | 5 |
| 5.18 | 1 | 45 | 20 | 15 | - | 10 | 5 | 10 |
| 5.18 | 2 | 20 | 35 | 5 | - | 15 | 10 | 5 |
| 5.19 | 1 | 40 | 25 | 10 | 10 | 15 | 10 | 15 |
| 5.19 | 2 | 25 | 15 | 5 | 5 | 10 | 15 | 5 |
| 5.20 | 1 | 20 | 35 | 5 | 15 | 10 | 15 | 5 |
| 5.20 | 2 | 35 | 25 | 10 | 15 | 5 | 15 | 10 |
| 5.21 | 1 | 25 | 40 | - | 10 | 5 | 15 | 10 |
| 5.21 | 2 | 35 | 20 | - | 5 | 10 | 10 | 15 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 5.22 | 1 | 30 | 30 | 10 | - | 15 | 10 | 5 |
| 5.22 | 2 | 15 | 25 | 5 | - | 10 | 5 | 10 |
| 5.23 | 1 | 20 | 15 | 10 | 10 | 5 | 15 | 15 |
| 5.23 | 2 | 30 | 20 | 10 | 15 | 5 | 10 | 15 |
| 5.24 | 1 | 25 | 35 | 5 | 5 | 10 | 15 | 10 |
| 5.24 | 2 | 20 | 45 | 15 | 15 | 10 | 5 | 10 |
| 5.25 | 1 | 35 | 20 | 15 | - | 15 | 10 | 5 |
| 5.25 | 2 | 35 | 40 | 10 | - | 5 | 10 | 15 |
Таблица 5.2
Варианты расчетного задания
| Вариант задания | Схема, подлежащая расчеты по методу: | |||||
| Уравнений Кирхгофа | Контурных токов | Наложения | ||||
| Схема (№ рисунка) | Вариант параметров | Схема (№ рисунка) | Вариант параметров | Схема (№ рисунка) | Вариант параметров | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 5.1 | 1 | 5.2 | 1 | 5.3 | 1 |
| 2 | 5.4 | 1 | 5.5 | 1 | 5.6 | 1 |
| 3 | 5.7 | 1 | 5.8 | 1 | 5.9 | 1 |
| 4 | 5.10 | 1 | 5.11 | 1 | 5.12 | 1 |
| 5 | 5.13 | 1 | 5.14 | 1 | 5.15 | 1 |
| 6 | 5.16 | 1 | 5.17 | 1 | 5.18 | 1 |
| 7 | 5.19 | 1 | 5.20 | 1 | 5.21 | 1 |
| 8 | 5.22 | 1 | 5.23 | 1 | 5.24 | 1 |
| 9 | 5.25 | 1 | 5.1 | 2 | 5.2 | 2 |
| 10 | 5.3 | 2 | 5.4 | 2 | 5.5 | 2 |
| 11 | 5.6 | 2 | 5.7 | 2 | 5.8 | 2 |
| 12 | 5.9 | 2 | 5.10 | 2 | 5.11 | 2 |
| 13 | 5.12 | 2 | 5.13 | 2 | 5.14 | 2 |
| 14 | 5.15 | 2 | 5.16 | 2 | 5.17 | 2 |
| 15 | 5.18 | 2 | 5.19 | 2 | 5.20 | 2 |
| 16 | 5.21 | 2 | 5.22 | 2 | 5.23 | 2 |
| 17 | 5.24 | 2 | 5.25 | 2 | 5.1 | 1 |
| 18 | 5.2 | 1 | 5.3 | 1 | 5.4 | 1 |
| 19 | 5.5 | 1 | 5.6 | 1 | 5.7 | 1 |
| 20 | 5.8 | 1 | 5.9 | 1 | 5.10 | 1 |
| 21 | 5.11 | 1 | 5.12 | 1 | 5.13 | 1 |
| 22 | 5.14 | 1 | 5.15 | 1 | 5.16 | 1 |
| 23 | 5.17 | 1 | 5.18 | 1 | 5.19 | 1 |
| 24 | 5.20 | 1 | 5.21 | 1 | 5.22 | 1 |
| 25 | 5.23 | 1 | 5.24 | 1 | 5.25 | 1 |
| 26 | 5.1 | 2 | 5.2 | 2 | 5.3 | 2 |
| 27 | 5.4 | 2 | 5.5 | 2 | 5.6 | 2 |
| 28 | 5.7 | 2 | 5.8 | 2 | 5.9 | 2 |
| 29 | 5.10 | 2 | 5.11 | 2 | 5.12 | 2 |
| 30 | 5.13 | 2 | 5.14 | 2 | 5.15 | 2 |
| 31 | 5.16 | 2 | 5.17 | 2 | 5.18 | 2 |
| 32 | 5.19 | 2 | 5.20 | 2 | 5.21 | 2 |
| 33 | 5.22 | 2 | 5.23 | 2 | 5.24 | 2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 34 | 5.25 | 2 | 5.1 | 1 | 5.2 | 1 |
| 35 | 5.3 | 1 | 5.4 | 1 | 5.5 | 1 |
| 36 | 5.6 | 1 | 5.7 | 1 | 5.8 | 1 |
| 37 | 5.9 | 1 | 5.10 | 1 | 5.11 | 1 |
| 38 | 5.12 | 1 | 5.13 | 1 | 5.14 | 1 |
| 39 | 5.15 | 1 | 5.16 | 1 | 5.17 | 1 |
| 40 | 5.18 | 1 | 5.19 | 1 | 5.20 | 1 |
| 41 | 5.21 | 1 | 5.22 | 1 | 5.23 | 1 |
| 42 | 5.24 | 1 | 5.25 | 1 | 5.1 | 2 |
| 43 | 5.2 | 2 | 5.3 | 2 | 5.4 | 2 |
| 44 | 5.5 | 2 | 5.6 | 2 | 5.7 | 2 |
| 45 | 5.8 | 2 | 5.9 | 2 | 5.10 | 2 |
| 46 | 5.11 | 2 | 5.12 | 2 | 5.13 | 2 |
| 47 | 5.14 | 2 | 5.15 | 2 | 5.16 | 2 |
| 48 | 5.17 | 2 | 5.18 | 2 | 5.19 | 2 |
| 49 | 5.20 | 2 | 5.21 | 2 | 5.22 | 2 |
| 50 | 5.23 | 2 | 5.24 | 2 | 5.25 | 2 |
Варианты схем для выполнения задания
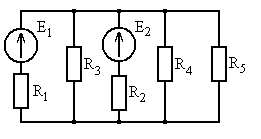
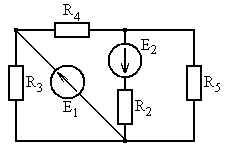
Рис. 5.1 Рис. 5.2
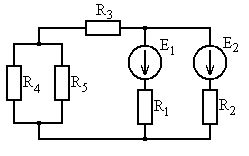
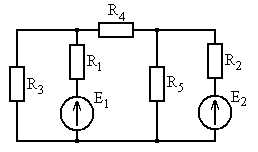
Рис. 5.3 Рис. 5.4
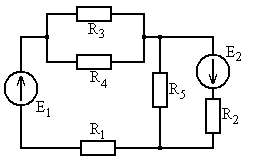
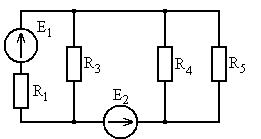
Рис. 5.5 Рис. 5.6
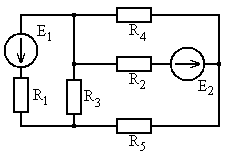
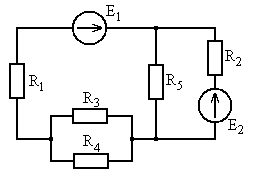
Рис. 5.7 Рис. 5.8
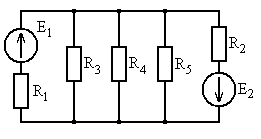
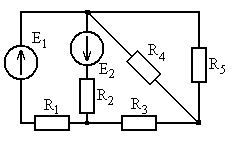
Рис. 5.9 Рис. 5.10
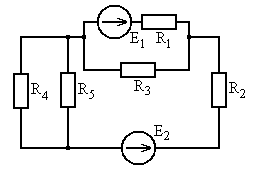
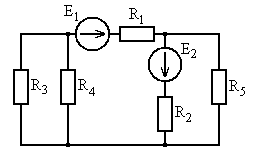
Рис. 5.11 Рис. 5.12
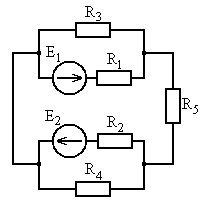
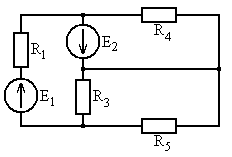
Рис. 5.13 Рис. 5.14
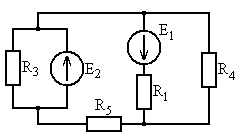
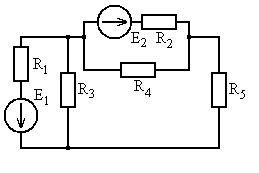
Рис. 5.15 Рис. 5.16
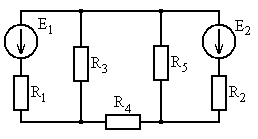
Рис. 5.17 Рис. 5.18
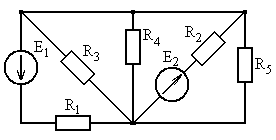
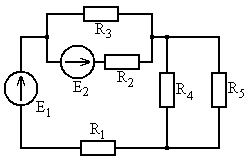
Рис. 5.19 Рис. 5.20
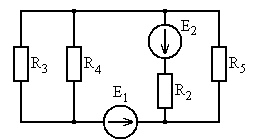
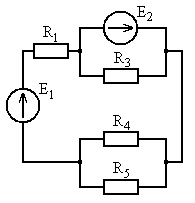
Рис. 5.21 Рис. 5.22
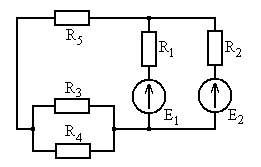
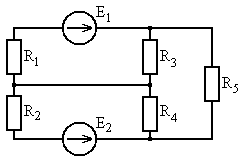
Рис. 5.23 Рис. 5.24
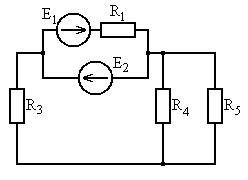
Рис. 5.25
Пример расчета сложных цепей постоянного тока.
1. Пример расчета цепи методом уравнений Кирхгофа.
В цепи, изображенной на рис. 5.26, заданы величины э.д.с. источников и сопротивления резисторов: Е1=100 В, Е2=75 В, R 1=10 Ом, R 2=15 Ом, R 3=20 Ом. Определить токи в ветвях схемы; проверку правильности решения произвести путем составления уравнения баланса мощностей цепи.
1.1. Произвольно направим токи во всех ветвях схемы (см. рис. 5.26).
1.2. Количество ветвей в схеме равно трем, следовательно, в схеме три различных тока. Для их нахождения следует составить три уравнения:
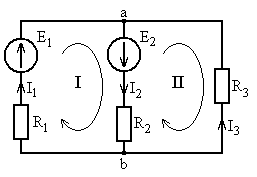
Рис. 5.26. Схема для расчета
одно по первому закону Кирхгофа (т.к. число узлов в схеме равно двум), и два по второму закону Кирхгофа. Для составления уравнений по второму закону Кирхгофа необходимо задать направления обхода соответствующих контуров (см. рис. 5.26).
1.3. Составим уравнение по первому закону Кирхгофа для узла «b». Токи, подтекающие к узлу, возьмем со знаком «–», вытекающие из узла – со знаком «+»:
.
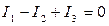В контуре I направление обхода совпадает с направлениями токов I 1, I 2 и э.д.с. Е1 и Е2, поэтому уравнение, составленное для данного контура по второму закону Кирхгофа, содержит слагаемые со знаком «+»:
.
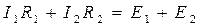В контуре II направление обхода не совпадает с направлениями токов I 2, I 3 и э.д.с. Е2, поэтому уравнение, составленное для данного контура по второму закону Кирхгофа, содержит слагаемые со знаком «–»:
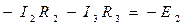
Получаемая таким образом система из трех уравнений с тремя неизвестными
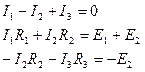
может быть решена любым удобным способом. Решение системы уравнений дает следующий результат: I 1 = 7,7 A; I2 = 6,5 A; I 3 = –1,2 А. Знак «–» для полученного значения тока I 3 означает, что истинное направление тока противоположно первоначально выбранному.
1.4. Произведем проверку правильности определения токов путем составления баланса мощностей цепи. В общем случае уравнение баланса мощностей имеет вид
,
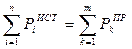где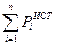 
– сумма мощностей источников энергии, имеющихся в электрической цепи, i – номер источника, n – общее количество источников; 
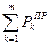– сумма мощностей, потребляемых приемниками (нагрузками), имеющимися в цепи, k – номер приемника, m – общее число приемников. При этом мощность источника э.д.с. определяется как произведение его э.д.с. на протекающий через источник ток; при совпадении направлений э.д.с. и тока указанное произведение входит в уравнение со знаком «+» (источник работает в режиме генератора энергии), а если направления э.д.с. и тока различны, их произведение входит в уравнение со знаком «–» (источник работает в режиме потребителя энергии). Мощность потребителя определяется как произведение его сопротивления на квадрат протекающего через него тока.
Таким образом, для рассматриваемой цепи уравнение баланса мощностей имеет вид
.
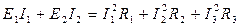После подстановки числовых значений получаем для левой части (суммарная мощность источников) 1257,5 Вт, для правой части (суммарная мощность приемников) 1255,5 Вт. Баланс мощностей сошелся, токи рассчитаны верно (некоторая разница числовых значений правой и левой частей уравнения баланса мощностей объясняется, в первую очередь, округлением результатов предыдущих вычислений; баланс мощностей считается сошедшимся, если разница правой и левой частей уравнения баланса мощностей не превышает 5%).
2. Пример расчета цепи методом контурных токов.
Пусть требуется рассчитать цепь, изображенную на рис. 5.26, методом контурных токов. Значения э.д.с. источников и сопротивления резисторов – те же, что и в предыдущем примере.
2.1. Выберем направления контурных токов I 11 и I 22 (см. рис. 5.27).
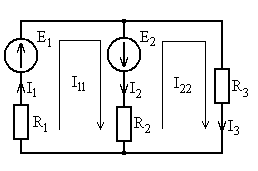
Рис. 5.27. Схема для расчета
2.2. Рассчитаем собственные и взаимные сопротивления контуров:
R 11 = R 1 + R 2 = 25 Ом;
R 22 = R 2 + R 3 = 35 Ом;
R 12 = R 21 = – R 2 = –15 Ом.
Взаимное сопротивление R 12 = R 21 берем со знаком «–», так как контурные токи в нем не совпадают по направлению.
Рассчитаем контурные э.д.с.:
Е11 = Е1 + Е2 = 175 В;
Е22 = –Е2 = –75 В.
Контурная э.д.с. Е22 имеет знак «–», так как направление контурного тока I 22 не совпадает с направлением э.д.с. Е2.
2.3. Система уравнений, составленных по второму закону Кирхгофа для контурных токов, для рассматриваемой цепи имеет вид:
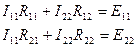
Решение данной системы дает следующий результат: I 11=7,7 A; I 22=1,2 А.
2.4. Найдем реальные токи в ветвях по величине и направлению:
I1 = I11 = 7,7 A;
I2 = I11 – I22 = 6,5 A;
I3 = I22 = 1,2 А.
2.5. Проверка правильности расчета токов может быть произведена путем составления уравнения баланса мощностей (так же, как это сделано в примере 1).
3. Пример расчета цепи методом наложения.
Пусть требуется рассчитать цепь, изображенную на рис. 5.26, методом наложения.
3.1. Как известно, принцип наложения позволяет расчленить сложную задачу на ряд более простых, в каждой из которых в рассматриваемой сложной цепи действует только одна э.д.с., а все остальные источники э.д.с. замыкаются накоротко (исключаются из схемы).
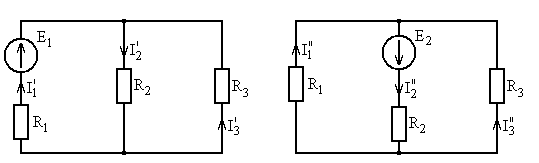
3.2. В рассматриваемой цепи имеются два источника э.д.с., следовательно, задача ее расчета распадается на две более простые задачи. Для их решения следует составить так называемые частичные схемы замещения, представленные на рис. 5.28. На рис. 5.28а изображена первая частичная схема, содержащая только источник э.д.с. Е1; по ветвям этой схемы протекают токи I׀1, I׀2, I׀3. На рис. 5.28б представлена вторая частичная схема с источником Е2 и токами I׀׀1, I׀׀2, I׀׀3.
а б
Рис. 5.28. Частичные схемы замещения
Получаемые таким способом частичные схемы могут быть рассчитаны любым удобным способом (проще всего схемы с одним источником энергии рассчитывать с помощью законов Ома и Кирхгофа); в результате расчета получают значения токов.
3.3. Реальные токи, протекающие в ветвях исходной схемы, находят путем алгебраического суммирования (суперпозиции) токов, протекающих в тех же ветвях каждой из частичных схем замещения, с учетом их направления. Для рассматриваемого случая реальные токи будут определены как
; 
; 
.
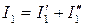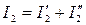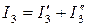3.4. Проверка правильности расчета токов может быть произведена путем составления уравнения баланса мощностей (так же, как это сделано в примере 1).
Задание 3. Расчет цепей переменного тока символическим методом
Задание: для электрической цепи переменного тока, соответствующей номеру варианта, с параметрами, приведенными в табл. 6.1, выполнить следующее:
1. Вычертить заданную цепь, выписать заданные величины э.д.с. и сопротивлений;
2. Построить схему замещения заданной цепи и определить полные комплексные сопротивления ветвей электрической цепи;
3. Произвести расчет всех комплексных токов и напряжений на участках цепи символическим методом;
4. Рассчитать сопряжённые комплексы токов;
5. Вычислить комплексы мощности источника и приёмников; произвести проверку правильности расчета токов путем составления уравнения баланса мощностей цепи;
6. Записать мгновенные значения токов и напряжений на участках цепи;
7. Построить векторную диаграмму токов и напряжений в комплексной плоскости.
Таблица 6.1
Варианты задания и параметры элементов схем
| Вари-ант | Схема (рис.)ис.) | Сопротивления элементов схемы, Ом | Параметры источника | ||||||||||
| R 1 | X 1 | R 2 | X 2 | R 3 | X 3 | R 4 | X 4 | R 5 | X 5 | U , В | ψ u , град | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 1 | 6.1 | 3 | 4 | 4 | 3 | 8 | 6 | 6 | 8 | 0 | 5 | 40 | 60 |
| 2 | 6.2 | 0 | 8 | 6 | 8 | 3 | 4 | 3 | 4 | 4 | 7 | 50 | 10 |
| 3 | 6.3 | 6 | 8 | 4 | 3 | 3 | 4 | 0 | 6 | 7 | 8 | 60 | 30 |
| 4 | 6.4 | 2 | 6 | 4 | 4 | 0 | 6 | 1 | 5 | 4 | 6 | 90 | 60 |
| 5 | 6.5 | 0 | 3 | 4 | 3 | 3 | 4 | 2 | 6 | 4 | 4 | 70 | 45 |
| 6 | 6.6 | 5 | 4 | 3 | 4 | 6 | 8 | 4 | 3 | 8 | 6 | 80 | 0 |
| 7 | 6.7 | 7 | 2 | 3 | 3 | 3 | 5 | 4 | 3 | 4 | 4 | 40 | 60 |
| 8 | 6.8 | 6 | 3 | 3 | 4 | 3 | 4 | 0 | 4 | 6 | 5 | 100 | 30 |
| 9 | 6.9 | 5 | 4 | 2 | 5 | 4 | 3 | 3 | 4 | 8 | 5 | 90 | 45 |
| 10 | 6.10 | 3 | 4 | 6 | 8 | 0 | 4 | 7 | 5 | 2 | 5 | 70 | 0 |
| 11 | 6.11 | 5 | 0 | 0 | 4 | 3 | 4 | 4 | 3 | 6 | 8 | 100 | 60 |
| 12 | 6.12 | 4 | 4 | 3 | 4 | 3 | 4 | 0 | 6 | 4 | 3 | 40 | 0 |
| 13 | 6.13 | 4 | 4 | 0 | 3 | 2 | 5 | 4 | 8 | 3 | 4 | 50 | 30 |
| 14 | 6.14 | 3 | 4 | 6 | 8 | 4 | 3 | 2 | 5 | 4 | 5 | 80 | 45 |
| 15 | 6.15 | 2 | 4 | 3 | 4 | 3 | 4 | 4 | 4 | 0 | 5 | 100 | 60 |
| 16 | 6.16 | 6 | 8 | 0 | 5 | 4 | 3 | 2 | 5 | 3 | 6 | 70 | 0 |
| 17 | 6.17 | 5 | 2 | 4 | 4 | 5 | 7 | 3 | 4 | 4 | 3 | 50 | 30 |
| 18 | 6.18 | 3 | 4 | 6 | 8 | 3 | 0 | 2 | 5 | 3 | 4 | 90 | 15 |
| 19 | 6.19 | 0 | 4 | 3 | 4 | 4 | 3 | 3 | 6 | 6 | 8 | 30 | 45 |
| 20 | 6.20 | 6 | 8 | 6 | 8 | 4 | 5 | 4 | 4 | 0 | 4 | 70 | 60 |
| 21 | 6.21 | 4 | 2 | 4 | 3 | 6 | 8 | 0 | 3 | 8 | 6 | 60 | 0 |
| 22 | 6.22 | 0 | 4 | 5 | 2 | 0 | 5 | 8 | 6 | 4 | 4 | 40 | 90 |
| 23 | 6.23 | 3 | 4 | 0 | 4 | 2 | 0 | 2 | 5 | 3 | 4 | 80 | 45 |
| 24 | 6.24 | 4 | 4 | 4 | 4 | 0 | 3 | 4 | 4 | 2 | 5 | 100 | 30 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 25 | 6.25 | 5 | 7 | 3 | 4 | 3 | 4 | 0 | 2 | 6 | 8 | 90 | 0 |
| 26 | 6.1 | 5 | 8 | 3 | 4 | 4 | 3 | 3 | 4 | 0 | 6 | 60 | 30 |
| 27 | 6.2 | 0 | 6 | 4 | 3 | 5 | 8 | 2 | 5 | 4 | 2 | 40 | 15 |
| 28 | 6.3 | 4 | 4 | 2 | 6 | 5 | 2 | 0 | 6 | 5 | 4 | 30 | 0 |
| 29 | 6.4 | 4 | 4 | 5 | 2 | 0 | 5 | 6 | 8 | 3 | 4 | 60 | 45 |
| 30 | 6.5 | 0 | 4 | 6 | 8 | 3 | 4 | 5 | 3 | 3 | 4 | 90 | 20 |
| 31 | 6.6 | 8 | 6 | 4 | 4 | 3 | 4 | 4 | 3 | 8 | 6 | 100 | 30 |
| 32 | 6.7 | 4 | 8 | 6 | 5 | 4 | 3 | 3 | 4 | 4 | 3 | 60 | 0 |
| 33 | 6.8 | 4 | 3 | 5 | 4 | 2 | 5 | 0 | 3 | 6 | 8 | 80 | 45 |
| 34 | 6.9 | 2 | 6 | 4 | 4 | 3 | 4 | 6 | 8 | 3 | 4 | 60 | 60 |
| 35 | 6.10 | 8 | 6 | 5 | 1 | 0 | 4 | 3 | 6 | 4 | 3 | 40 | 90 |
| 36 | 6.11 | 4 | 0 | 0 | 3 | 4 | 6 | 3 | 4 | 6 | 8 | 80 | 30 |
| 37 | 6.12 | 3 | 5 | 6 | 8 | 4 | 3 | 0 | 2 | 4 | 4 | 50 | 20 |
| 38 | 6.13 | 5 | 2 | 0 | 4 | 3 | 4 | 3 | 4 | 6 | 8 | 60 | 60 |
| 39 | 6.14 | 4 | 4 | 3 | 4 | 2 | 5 | 6 | 8 | 3 | 6 | 90 | 30 |
| 40 | 6.15 | 4 | 4 | 8 | 6 | 3 | 4 | 2 | 5 | 0 | 4 | 80 | 0 |
| 41 | 6.16 | 2 | 5 | 0 | 2 | 3 | 4 | 4 | 2 | 7 | 4 | 50 | 20 |
| 42 | 6.17 | 6 | 8 | 3 | 4 | 6 | 2 | 3 | 4 | 4 | 2 | 100 | 60 |
| 43 | 6.18 | 4 | 3 | 6 | 2 | 3 | 0 | 6 | 8 | 3 | 4 | 40 | 90 |
| 44 | 6.19 | 0 | 4 | 3 | 4 | 2 | 5 | 8 | 2 | 8 | 6 | 70 | 20 |
| 45 | 6.20 | 3 | 4 | 2 | 5 | 3 | 2 | 3 | 4 | 0 | 8 | 50 | 45 |
| 46 | 6.21 | 6 | 3 | 4 | 4 | 2 | 5 | 0 | 6 | 3 | 4 | 90 | 60 |
| 47 | 6.22 | 0 | 2 | 3 | 4 | 0 | 8 | 2 | 5 | 3 | 4 | 80 | 30 |
| 48 | 6.23 | 6 | 8 | 0 | 5 | 4 | 0 | 5 | 2 | 4 | 3 | 100 | 0 |
| 49 | 6.24 | 3 | 4 | 4 | 3 | 0 | 6 | 8 | 6 | 3 | 4 | 60 | 20 |
| 50 | 6.25 | 2 | 5 | 4 | 3 | 6 | 8 | 0 | 4 | 2 | 5 | 50 | 45 |
Варианты схем для выполнения задания
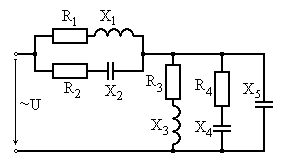
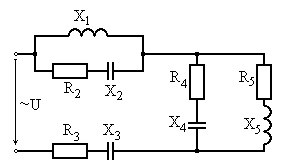
Рис. 6.1 Рис. 6.2
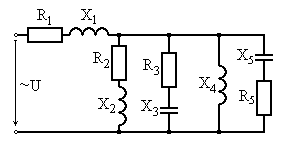
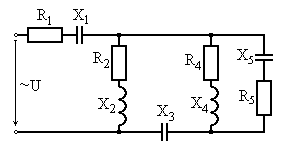
Рис. 6.3 Рис. 6.4
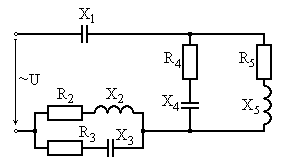
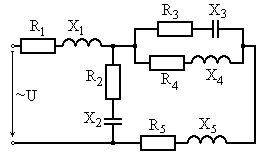
Рис. 6.5 Рис. 6.6
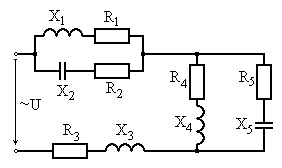
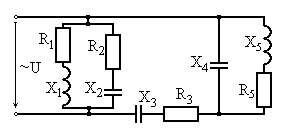
Рис. 6.7 Рис. 6.8
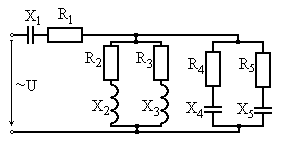
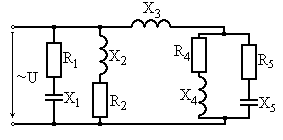
Рис. 6.9 Рис. 6.10
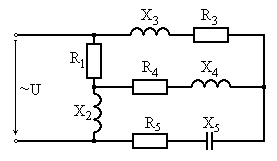
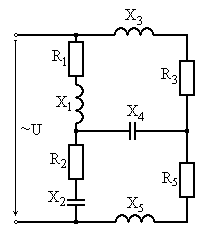
Рис. 6.11 Рис. 6.12
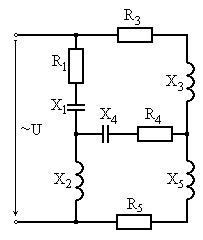
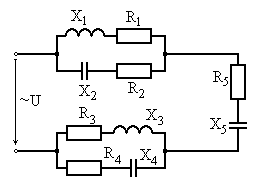
Рис. 6.13 Рис. 6.14
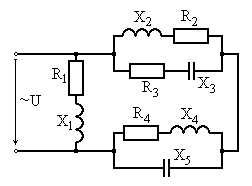
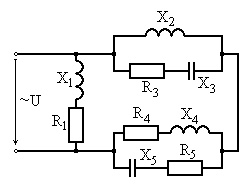
Рис. 6.15 Рис. 6.16
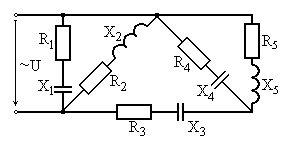
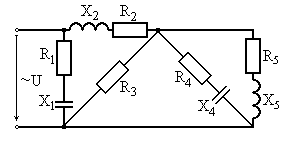
Рис. 6.17 Рис. 6.18
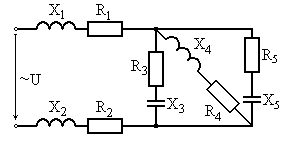
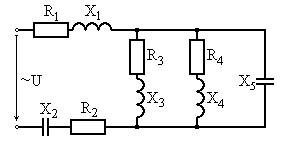
Рис. 6.19 Рис. 6.20
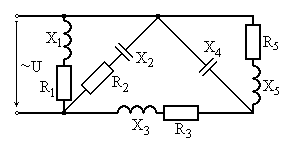
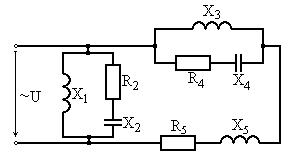
Рис. 6.21 Рис. 6.22
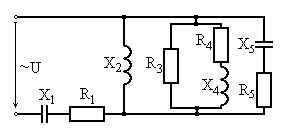
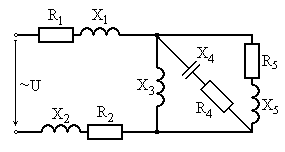
Рис. 6.23 Рис. 6.24
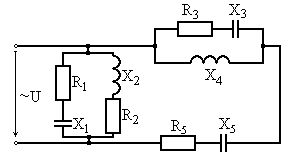
Рис. 6.25
Пример расчета простой цепи переменного тока символическим методом.
1. Пусть задана схема, изображенная на рис. 6.26, с параметрами: R1 = 5 Ом; R2 = 10 Ом; R3 = 4 Ом; R4 = 8 Ом; R5 = 6 Ом; X1 = 8 Ом; X2 = 6 Ом; X3 = 10 Ом; X4 = 10 Ом; X5 = 5 Ом; параметры источника: U = 220 B, ψu = 450.
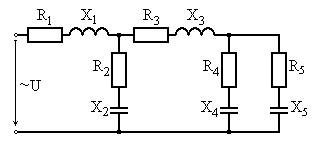
Рис. 6.26. Исходная цепь для расчета
2. Строим схему замещения (рис. 6.27) и определяем комплексные сопротивления ветвей и комплекс входного напряжения. На схеме замещения обозначим условные положительные направления токов в ветвях.
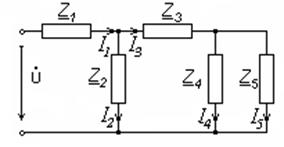
Рис. 6.27. Схема замещения исходной цепи
Полные комплексные сопротивления ветвей схемы замещения:
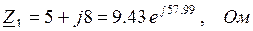– сопротивление имеет активно-индуктивный (R-L) характер;
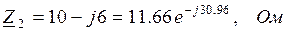– сопротивление имеет активно-емкостный (R-C) характер;
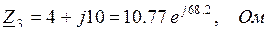– сопротивление имеет активно-индуктивный (R-L) характер;
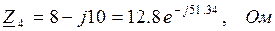– сопротивление имеет активно-емкостный (R-C) характер;
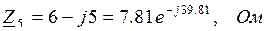– сопротивление имеет активно-емкостный (R-C) характер.
Комплекс входного напряжения:
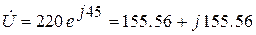, В.
3. Произведем расчет комплексных токов и напряжений на всех участках цепи символическим методом. Для этого найдем комплекс эквивалентного сопротивления всей цепи (т.е. приведем ее к виду, представленному на рис. 6.28).
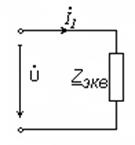
Рис. 6.28. Схема с эквивалентным сопротивлением
Определим эквивалентные сопротивления (сначала отдельных участков схемы замещения, а затем эквивалентное сопротивление всей цепи):
;
;
;
.
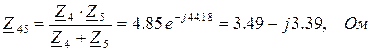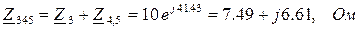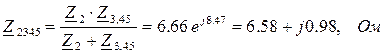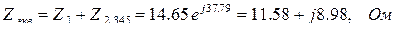Комплексы токов в ветвях можно найти как:
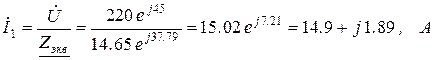
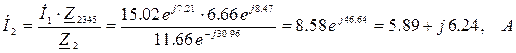
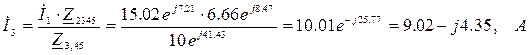
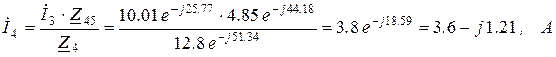
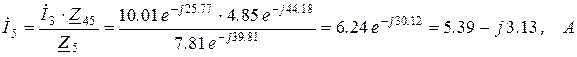
Комплексы напряжений на участках цепи:
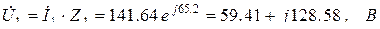
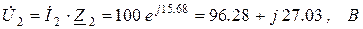
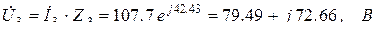
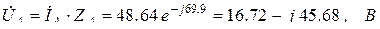
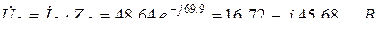
4. Найдем сопряженные комплексы токов:
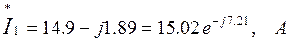
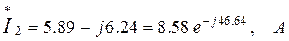
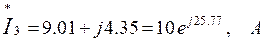
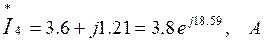
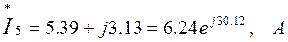
5. Вычислим комплексы мощностей источника и приемников. Составим уравнение баланса мощностей и убедимся в правильности произведенных расчетов.
Мощность приемников:
,
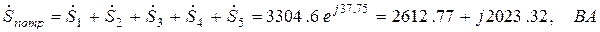где
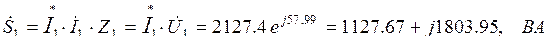
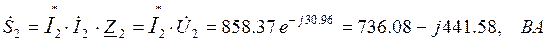
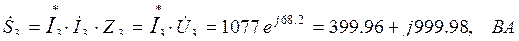
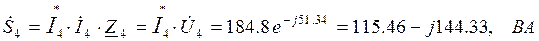
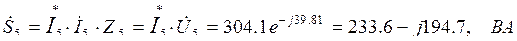
Мощность источника
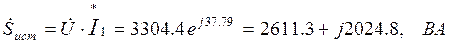
Баланс мощностей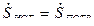 
сошелся, погрешность не превышает допустимую величину в 5%.
6. Мгновенные значения токов и напряжений на участках цепи, в общем виде, выражаются как
, 
,
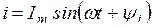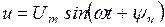где: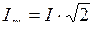 
– амплитудное значение тока;
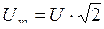– амплитудное значение напряжения.
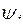– начальная фаза тока;
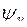– начальная фаза напряжения.
Найдем мгновенные значения токов ветвей:
,
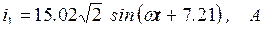
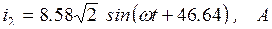
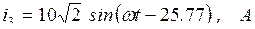
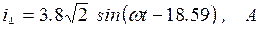
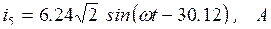а также мгновенные значения напряжений на участках цепи:
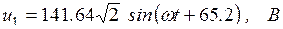
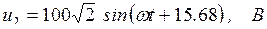
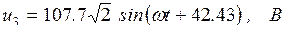
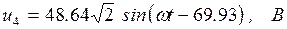
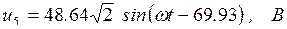
7. Строим векторную диаграмму токов и напряжений в комплексной плоскости (рис. 6.29).
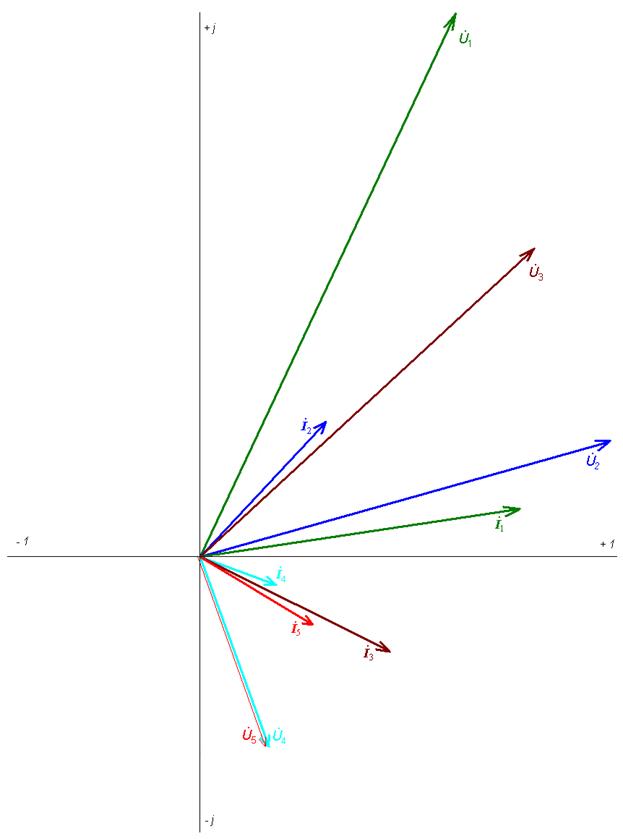
Рис. 6.29. Векторная диаграмма токов и напряжений
Задание 4. Расчет трехфазных цепей
Задание: для электрической цепи трехфазного переменного тока, соответствующей номеру варианта, с параметрами, приведенными в таблице 7.1, выполнить следующее:
1. Вычертить заданную цепь, выписать заданные величины э.д.с. и сопротивлений;
2. Построить схему замещения заданной цепи и определить полные комплексные сопротивления каждой из фаз нагрузки;
3. Произвести расчет комплексных фазных и линейных токов, а также тока в нейтральном проводе (при его наличии в заданной схеме), комплексных напряжений на каждом из элементов всех фаз нагрузки;
4. Найти активную, реактивную и полную мощности каждой фазы и всей цепи; произвести проверку правильности расчета токов путем составления уравнения баланса мощностей цепи;
5. Записать мгновенные значения токов и напряжений на каждом из элементов всех фаз нагрузки;
6. Построить векторную диаграмму токов и напряжений в комплексной плоскости.
7. При выполнении задания по каждому из вариантов принять, что заданная схема питается от симметричного трехфазного источника э.д.с., при этом действующее значение э.д.с. каждой из фаз источника равно 220 В.
Таблица 7.1
Варианты задания и параметры элементов схем
| Вариант задания | Схема (№ рисунка) | Параметры элементов схемы, Ом | |||||
| Ra (Rab) | Xa (Xab) | Rb (Rbc) | Xb (Xbc) | Rc (Rca) | Xc (Xca) | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 7.1 | 5 | 3 | 5 | 8 | 7 | 4 |
| 2 | 7.2 | 4 | – | 2 | 10 | 8 | 5 |
| 3 | 7.3 | 3 | 6 | – | 5 | 7 | 7 |
| 4 | 7.4 | 10 | 8 | – | 3 | 2 | 5 |
| 5 | 7.5 | 6 | 5 | 7 | 4 | 10 | 10 |
| 6 | 7.6 | 5 | 4 | 5 | – | – | 8 |
| 7 | 7.7 | – | 9 | – | 5 | 10 | 7 |
| 8 | 7.8 | 7 | 8 | 4 | 4 | 10 | 5 |
| 9 | 7.9 | 10 | 3 | 8 | 5 | 6 | 7 |
| 10 | 7.10 | 8 | 4 | – | 5 | – | 9 |
| 11 | 7.11 | 3 | 2 | 10 | 10 | 7 | 4 |
| 12 | 7.12 | – | 5 | 6 | 10 | 9 | 3 |
| 13 | 7.13 | 6 | 6 | 2 | 4 | 5 | 3 |
| 14 | 7.14 | – | 3 | 8 | 5 | 7 | 9 |
| 15 | 7.15 | 10 | 10 | – | 6 | 4 | 8 |
| 16 | 7.16 | 8 | 4 | 3 | 7 | 5 | 5 |
| 17 | 7.17 | 5 | 8 | – | 2 | 3 | 4 |
| 18 | 7.18 | 7 | 4 | – | 3 | 10 | 9 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 19 | 7.19 | – | 3 | 8 | 5 | 9 | 6 |
| 20 | 7.20 | 5 | 7 | – | 3 | – | 8 |
| 21 | 7.21 | 5 | 8 | 10 | 3 | 7 | 4 |
| 22 | 7.22 | – | 4 | – | 7 | 5 | 3 |
| 23 | 7.23 | 7 | 2 | 10 | 5 | 8 | 3 |
| 24 | 7.24 | – | 5 | – | 3 | 10 | 7 |
| 25 | 7.25 | – | 7 | 9 | 7 | – | 4 |
| 26 | 7.1 | 10 | 3 | 8 | 6 | 5 | 9 |
| 27 | 7.2 | 8 | – | 5 | 4 | 5 | 6 |
| 28 | 7.3 | 6 | 3 | – | 8 | 4 | 10 |
| 29 | 7.4 | 4 | 8 | – | 6 | 4 | 2 |
| 30 | 7.5 | 7 | 10 | 5 | 8 | 3 | 4 |
| 31 | 7.6 | 8 | 3 | 6 | – | – | 4 |
| 32 | 7.7 | – | 6 | – | 10 | 3 | 5 |
| 33 | 7.8 | 5 | 2 | 10 | 10 | 7 | 5 |
| 34 | 7.9 | 3 | 5 | 5 | 7 | 9 | 2 |
| 35 | 7.10 | 9 | 10 | – | 8 | – | 3 |
| 36 | 7.11 | 5 | 8 | 4 | 10 | 10 | 4 |
| 37 | 7.12 | – | 4 | 8 | 5 | 7 | 3 |
| 38 | 7.13 | 9 | 5 | 10 | 6 | 8 | 4 |
| 39 | 7.14 | – | 5 | 6 | 6 | 10 | 3 |
| 40 | 7.15 | 7 | 6 | – | 5 | 9 | 3 |
| 41 | 7.16 | 7 | 7 | 5 | 3 | 9 | 4 |
| 42 | 7.17 | 8 | 7 | – | 10 | 9 | 5 |
| 43 | 7.18 | 6 | 8 | – | 10 | 5 | 8 |
| 44 | 7.19 | – | 5 | 4 | 8 | 7 | 2 |
| 45 | 7.20 | 10 | 4 | – | 5 | – | 3 |
| 46 | 7.21 | 7 | 10 | 6 | 2 | 5 | 5 |
| 47 | 7.22 | – | 10 | – | 2 | 7 | 4 |
| 48 | 7.23 | 10 | 8 | 5 | 7 | 2 | 3 |
| 49 | 7.24 | – | 3 | – | 8 | 7 | 3 |
| 50 | 7.25 | – | 9 | 5 | 3 | – | 8 |
Варианты схем для выполнения задания
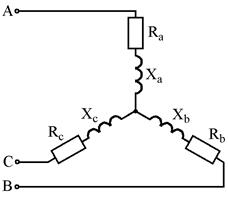
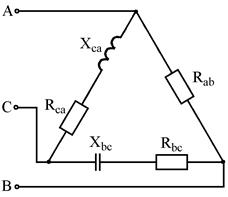
Рис. 7.1 Рис. 7.2
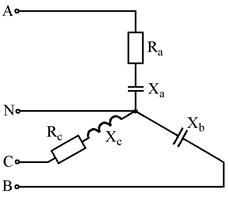
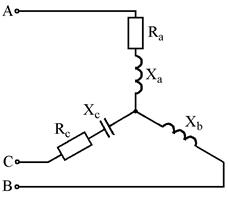
Рис. 7.3 Рис. 7.4
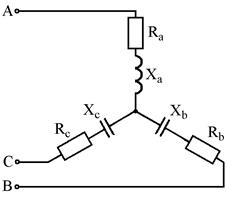
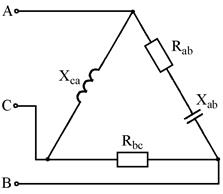
Рис. 7.5 Рис. 7.6
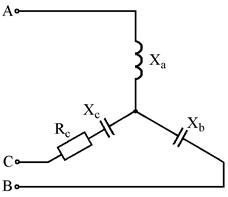
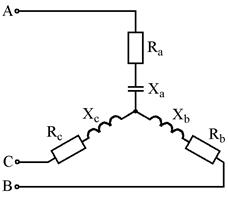
Рис. 7.7 Рис. 7.8
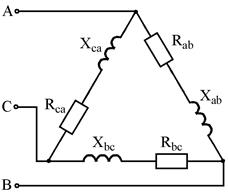
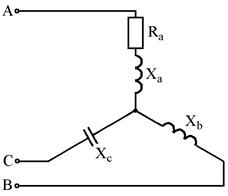
Рис. 7.9 Рис. 7.10
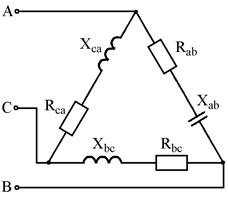
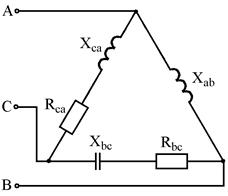
Рис. 7.11 Рис. 7.12
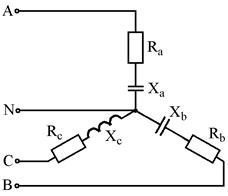
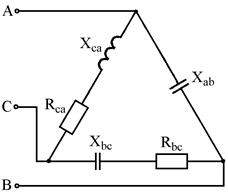
Рис. 7.13 Рис. 7.14
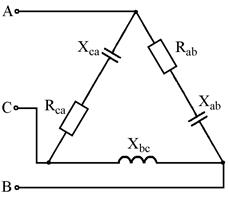
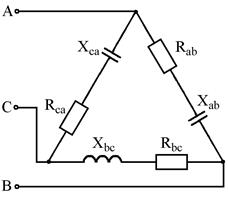
Рис. 7.15 Рис. 7.16
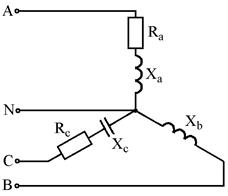
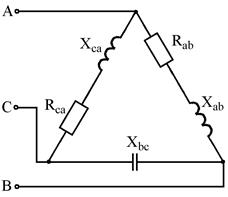
Рис. 7.17 Рис. 7.18
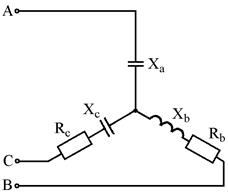
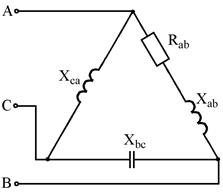
Рис. 7.19 Рис. 7.20
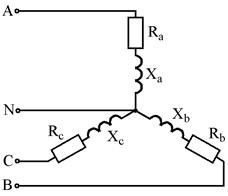
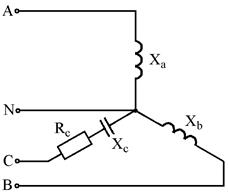
Рис. 7.21 Рис. 7.22
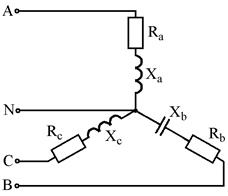
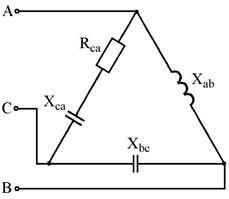
Рис. 7.23 Рис. 7.24
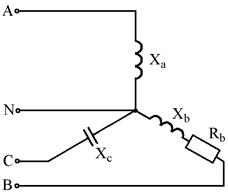
Рис. 7.25
Примеры расчета трехфазных цепей.
Пример 1.
В трехфазную сеть с линейным напряжением U л=220 В включен приемник, соединенный треугольником, сопротивление каждой фазы которого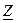 
=(10 + j10) Ом (рис. 7.26).
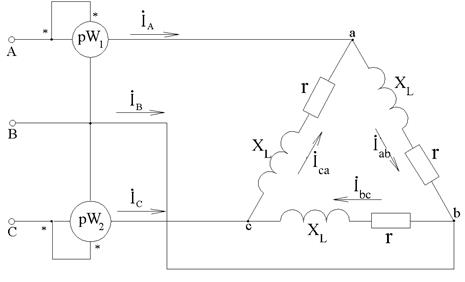
Рис. 7.26. Схема для расчета
Требуется найти токи в каждой фазе нагрузки, токи в линейных проводах и показания каждого ваттметра. Построить векторную диаграмму токов и напряжений.
Решение. Расчет токов в трехфазных цепях производится символическим методом. Примем, что вектор линейного напряжения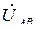 
направлен по действительной оси, тогда 
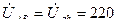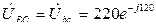В,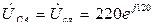 
В, 
В.
Определяем фазные токи:
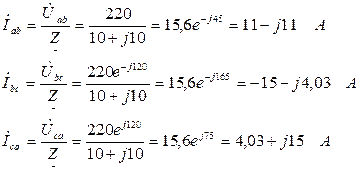
Находим линейные токи:
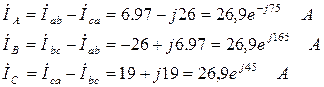
Определим показания ваттметров:
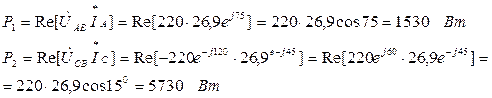
Активная мощность цепи (алгебраическая сумма показаний ваттметров) Р равна:
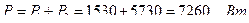или
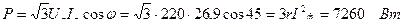
На рис. 7.27 приведена векторная диаграмма напряжений и токов.
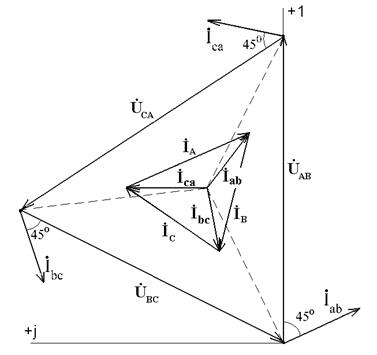
Рис. 7.27. Векторная диаграмма
Пример 2.
В четырехпроводную трехфазную сеть с линейным напряжением U л=220 В включен по схеме «звезда с нулевым проводом» приемник, активные и индуктивные сопротивления фаз которого соответственно равны: ra =3 Ом, xa=4 Ом, rb =3 Ом, xb =5,2 Ом, rc=4 Ом, xc=3 Ом (рис. 7.28).
Требуется определить токи в линейных и нейтральном проводах и построить векторную диаграмму токов и напряжений.
Решение. Считаем, что вектор фазного напряжения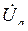 
направлен по действительной оси, тогда
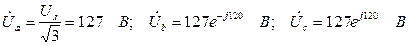
Находим линейные токи:
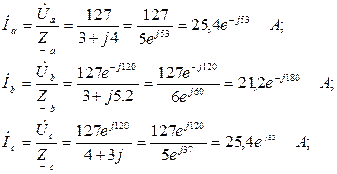
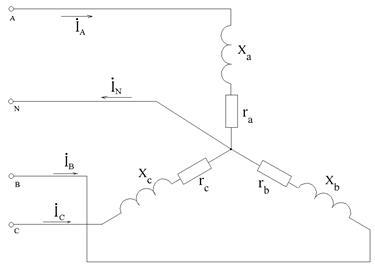
Рис. 7.28. Схема для расчета
Ток в нейтральном проводе определяется как геометрическая сумма линейных токов:
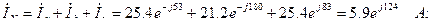
Векторная диаграмма приведена на рис. 7.29.
При несимметричной нагрузке для определения активной мощности находят мощность каждой фазы отдельно:
,
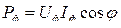а мощность всей трехфазной системы получают как сумму мощностей всех фаз.
Пример 3.
В трехфазную сеть с линейным напряжением U л=380 В включен по схеме «звезда» приемник, активное, индуктивное и емкостное сопротивление фаз которого равны r=xL=xC=22 Ом (рис. 7.30).
Решение. Расчет токов производим символическим методом. Находим фазные напряжения:
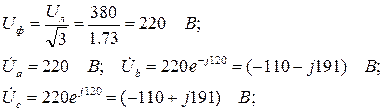
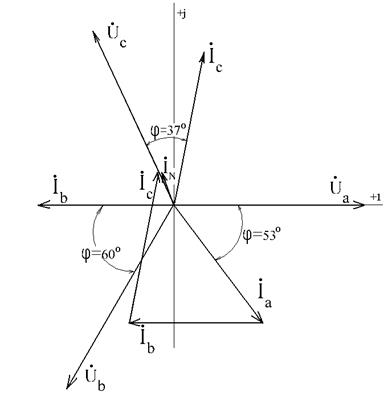
Рис. 7.29. Векторная диаграмма
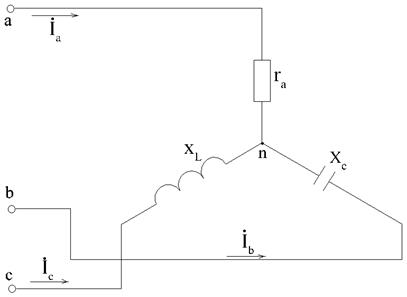
Рис. 7.30. Схема для расчета
Определяем напряжение между нейтральными точками приемника и источника питания:
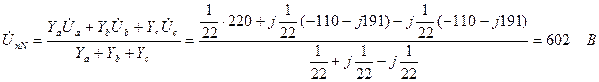
Определяем напряжения на зажимах фаз приемника:
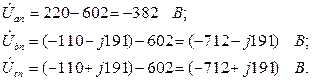
Определяем фазные (линейные) токи:
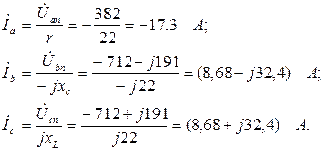
Векторная диаграмма изображена на рис. 7.31.
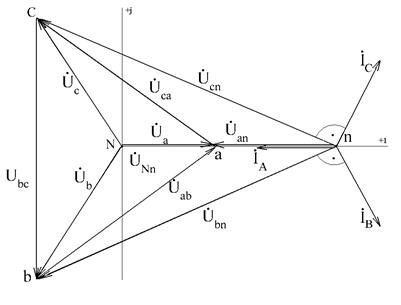
Рис. 7.31. Векторная диаграмма
Из рассмотрения этой задачи следует, что напряжения на зажимах фаз приемника получаются неодинаковыми. Поэтому несимметричные приемники (бытовые и др.) соединяют либо четырехпроводной звездой, либо треугольником.
Литература
1. Касаткин А.С., Немцов М.В. Электротехника. Учебник для ВУЗов. М.: Издательский центр «Академия», 2003, 544 с.
2. Немцов М.В., Светлакова И.И. Электротехника. Ростов-на-Дону: «Феникс», 2004, 567 с.
3. Прянишников В.А., Петров Е.А., Осипов Ю.М. Электротехника и ТОЭ в примерах и задачах. Практическое пособие. СПб.: «Корона принт», 2001, 336 с.
4. Рекус Г.Г. Основы электротехники и электроники в задачах с решениями. Учебное пособие. М.: Высшая школа, 2005, 343 с.
5. Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей. М.: Высшая школа, 1990, 544 с.
6. Черевко А.И. Линейные электрические цепи. Северодвинск: РИО Севмашвтуза, 2007, 78 с.
7. Зевеке Г.В., Ионкин П.А., Нетушин А.В., Страхов С.В. Основы теории цепей. М.: Энергоатомиздат, 1989, 528 с.
Содержание
Общие требования к выполнению контрольных работ ……………………3
1. Расчет цепей постоянного тока (общие сведения) ………………………4
1.1. Основные понятия. Источники электрической энергии ………………4
1.2. Закон Ома ………………………………………………………………...5
1.3. Законы Кирхгофа …………………………………………………….…..6
1.4. Основные методы расчета цепей постоянного тока …………………..7
2. Cведения из теории цепей переменного тока ……………………………13
2.1. Основные понятия и определения ………………………………….…..13
2.2. Изображение синусоидальной функции комплексным числом. Символический метод расчета цепей синусоидального тока ………….….15
2.3. Элементы электрической цепи переменного тока ………………….…17
2.4. Законы Ома и Кирхгофа в комплексной форме записи ………………18
2.5. Последовательное и параллельное соединение сопротивлений и проводимостей …………………………………………………………….....18
2.6. О применимости методов расчета цепей постоянного тока к расчетам цепей синусоидального тока ………………………………………………...19
2.7. Мощность в цепи синусоидального тока …………………………..…..19
2.8. Треугольники токов, напряжений, сопротивлений, проводимостей и мощностей ……………………………………………………………….…...20
2.9. Векторные и топографические диаграммы ……………………….…...20
3. Основные сведения по расчету трехфазных цепей ………………….….21
3.1. Термины и определения ………………………………………….……..21
3.2. Основные схемы соединения трехфазных цепей …………………......23
3.3. Расчет трехфазных систем …………………………………………...…24
3.4. Мощность в трехфазных системах ………………………………...…..27
4. Задание 1. Расчет простых цепей постоянного тока ………………....…28
5. Задание 2. Расчет сложных цепей постоянного тока ………………..….34
6. Задание 3. Расчет цепей переменного тока символическим методом ....44
7. Задание 4. Расчет трехфазных цепей ………………………………..…...53
Черевко Александр Иванович
Ивлев Марк Леонидович
Федотова Алла Александровна
Дата: 2018-12-21, просмотров: 616.
