Существует два основных способа соединения обмоток генераторов, трансформаторов и приемников в трехфазных цепях: соединение звездой и соединение треугольником. Соединение генератора и приемника звездой показано на рис. 3.2, а соединение треугольником – на рис. 3.3.
При соединении звездой все «концы» фазных обмоток генератора и нагрузки соединяют в одну точку. Общие точки обмоток генератора и ветвей звезды нагрузки называются нейтральными (нулевыми), а соединяющий их провод – нейтралью (нулевым проводом). При соединении треугольником фазные обмотки генератора соединяются таким образом, чтобы «начало» одной обмотки соединялось с «концом» другой обмотки. Общие точки каждой пары фазных обмоток генератора и ветвей приемника соединяются проводами, носящими названия линейных проводов. Трехфазная цепь и трехфазный приемник называются симметричными, если комплексные сопротивления всех фаз одинаковы. В противном случае они называются несимметричными. Режим работы, при котором трехфазные системы напряжений и токов симметричны, называют симметричным режимом.
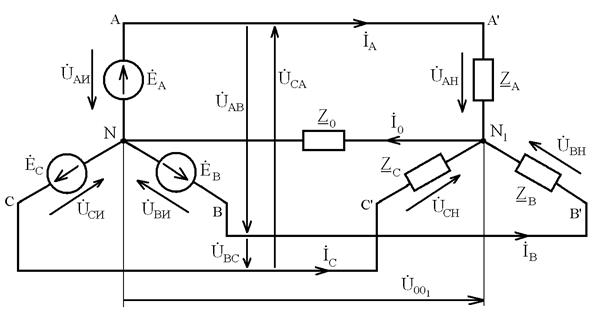
Рис. 3.2. Соединение фаз источника и нагрузки в звезду
Между линейными и фазными напряжениями и токами в симметричной трехфазной системе существуют следующие соотношения.
1) При соединении в звезду (рис. 3.2):
Iл=Iф; Uл= 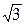 Uф.
Uф.
2) При соединении в треугольник (рис. 3.3):
Uл=Uф; Iл= 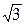 Iф.
Iф.
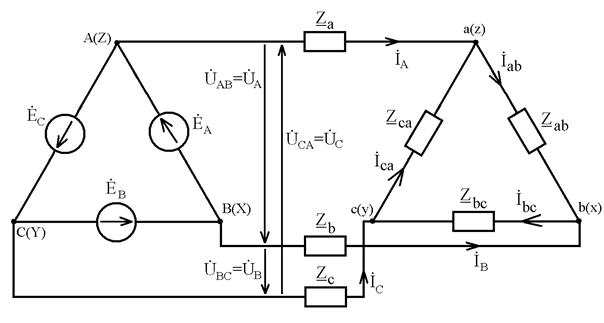
Рис. 3.3. Соединение фаз источника и нагрузки в треугольник
Расчет трехфазных систем.
Трехфазные цепи являются разновидностью цепей синусоидального тока, поэтому расчет и исследование процессов в них производятся при помощи символического метода и сопровождается построением векторных и топографических диаграмм.
Расчет симметричных трехфазных цепей производится только для одной фазы системы, так как здесь IА=IВ=IС; ZА=ZВ=ZС; j А = j В = j С, т.е. имеет место полная симметрия. В этом случае при соединении звездой (рис. 3.2) линейные напряжения равны разностям соответствующих фазных напряжений:
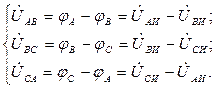
а при соединении треугольником (рис. 3.3) линейные токи равны разностям соответствующих фазных токов:
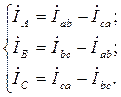
На рис. 3.4 и 3.5 представлены топографические векторные диаграммы (ТВД) для случаев соединения фаз приемника звездой и треугольником соответственно.
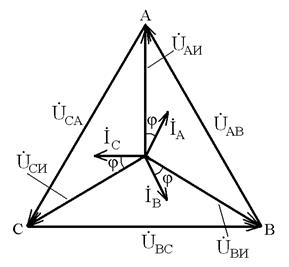
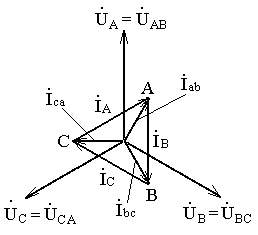
Рис. 3.4. ТВД для соединения Рис. 3.5. ТВД для соединения
фаз приемника звездой фаз приемника треугольником
Расчет несимметричных трехфазных цепей при соединении в звезду и звезду с нулевым проводом следует начинать с определения напряжения смещения нейтрали:
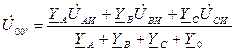 , (3.1)
, (3.1)
где 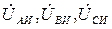 – фазные напряжения источника;
– фазные напряжения источника; 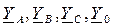 – проводимости фаз нагрузки и нулевого провода.
– проводимости фаз нагрузки и нулевого провода.
Токи в фазах нагрузки и нейтральном проводе:
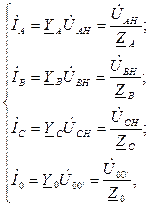
причем фазные напряжения в несимметричной нагрузке равны
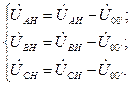
Если нагрузка соединена в звезду без нулевого провода, то 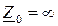 и в (3.1) следует принять
и в (3.1) следует принять 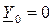 .
.
Если известны (в случае 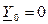 ) линейные напряжения
) линейные напряжения 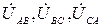 и проводимости фаз нагрузки, то фазные напряжения нагрузки можно найти по формулам:
и проводимости фаз нагрузки, то фазные напряжения нагрузки можно найти по формулам:
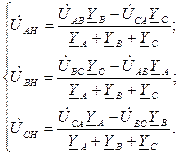
Порядок расчета несимметричной нагрузки с соединением фаз в треугольник зависит от учета либо неучета сопротивлений в линейных проводах (рис. 3.6).
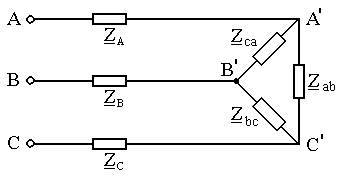
Рис. 3.6. Несимметричная нагрузка с соединением фаз в треугольник
Если известны линейные напряжения между зажимами A ¢, B ¢, C ¢, к которым присоединены сопротивления приемника, то задача определения токов в нагрузке решается по закону Ома, а затем находятся токи в линейных проводах. Однако обычно бывают известны напряжения на зажимах A, B, C источника питания, поэтому расчет несколько усложняется. Проще всего его провести, заменяя треугольник сопротивлений эквивалентной звездой. Определив токи в линейных проводах, нетрудно определить фазные напряжения приемника в эквивалентной звезде и получить линейные напряжения на фазах приемника как разность фазных напряжений эквивалентной звезды, а затем вычислить токи в ветвях треугольника нагрузки. Формулы преобразования звезды сопротивлений ( 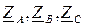 ) в эквивалентный треугольник сопротивлений (
) в эквивалентный треугольник сопротивлений ( 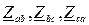 ) и обратно имеют вид:
) и обратно имеют вид:
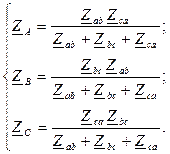
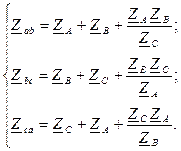
Дата: 2018-12-21, просмотров: 786.