1.4.1. Метод уравнений Кирхгофа.

Любая электрическая цепь может быть рассчитана на основании законов Кирхгофа. Рассмотрим алгоритм использования метода для нахождения токов в ветвях схемы.

Обозначим число всех ветвей схемы через m, число ветвей, содержащих источники тока, – через m_ит и число узлов – через n. Так как токи в ветвях с источниками тока известны (они равны токам источников тока), то число неизвестных токов равняется m–m_ит. Далее следует придерживаться нижеприведенного порядка действий:

а) произвольно выбрать положительные направления токов в ветвях и обозначить их на схеме;

б) выбрать положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа;

в) составить необходимое количество уравнений по первому закону Кирхгофа для узлов цепи;

г) составить необходимое количество уравнений по второму закону Кирхгофа для контуров цепи.

Чтобы получить линейно независимые уравнения, по первому закону Кирхгофа составляют число уравнений, равное числу узлов без единицы, то есть (n–1) уравнений. По второму закону Кирхгофа составляют число уравнений, равное числу ветвей без источников тока (m–m_ит), за вычетом числа уравнений, составленных по первому закону Кирхгофа, то есть (m–m_ит)–(n–1)=(m–m_ит–n+1) уравнений.

Составляя уравнения по второму закону Кирхгофа, надо охватить все ветви схемы, исключая ветви с источниками тока. При записи линейно независимых уравнений по второму закону Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону Кирхгофа. Такие контуры называются независимыми.

1.4.2. Метод контурных токов.

При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов (по второму закону Кирхгофа), после чего определяют реальные токи ветвей через контурные токи.

Таким образом, метод контурных токов можно определить как метод расчета, в котором за искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по второму закону Кирхгофа при расчете этой схемы рассмотренным выше методом.

При использовании данного метода выбирают и обозначают контурные токи, при этом по любой ветви должен проходить хотя бы один выбранный контурный ток. Известно, что общее число контурных токов k=m–m_ит–n+1. Для определения контурных токов по второму закону Кирхгофа составляют k уравнений в виде:

                       ,

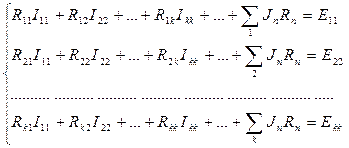где R_nn – собственное контурное сопротивление n – го контура (сумма сопротивлений всех ветвей, входящих в контур n); R_nl – взаимное контурное сопротивление смежных контуров n и l, причем R_nl=R_ln; если направления контурных токов в общей ветви для контуров n и l совпадают, то R_nl положительно, в противном случае R_nl отрицательно; E_nn – контурная э.д.с. контура n, она равна алгебраической сумме э.д.с., включенных в ветви, образующие данный контур; R_n – общее сопротивление ветви контура n с контуром, содержащим источник тока J_n.

    Для единообразия в знаках сопротивлений рекомендуется все контурные токи направлять в одну и ту же сторону (например, по часовой стрелке).

1.4.3. Метод узловых потенциалов.

Если электрическая схема имеет большое количество ветвей и малое количество узлов, то для ее расчета целесообразно применять метод узловых потенциалов, в котором за неизвестные принимают потенциалы узлов схемы.

Данный метод, основанный на использовании первого закона Кирхгофа и закона Ома для участка цепи, содержащего источник э.д.с., позволяет уменьшить количество уравнений получающейся системы до числа t, равного количеству узлов схемы без одного, t=n–1.

Сущность метода заключается в том, что вначале составляются уравнения по первому закону Кирхгофа для (n–1) узлов схемы, а затем токи в ветвях выражаются через потенциалы узлов и проводимости соответствующих ветвей:

.

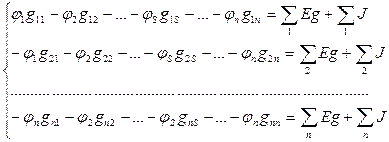Здесь g_ss – сумма проводимостей ветвей, присоединенных к узлу s; g_sq – сумма проводимостей ветвей, непосредственно соединяющих узел s с узлом q; 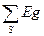 – алгебраическая сумма произведений э.д.с. ветвей, примыкающих к узлу s, на их проводимости; при этом со знаком плюс берутся те э.д.с., которые действуют в направлении узла s, и со знаком минус – в направлении от узла s;  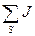– алгебраическая сумма токов источников тока, присоединенных к узлу s; при этом со знаком плюс берутся те токи, которые направлены к узлу s, а со знаком минус – в направлении от узла s.

Решая полученную систему, находят потенциалы (n–1) узлов, а затем токи в ветвях по закону Ома.

Методом узловых потенциалов рекомендуется пользоваться в тех случаях, когда число уравнений будет меньше числа уравнений, составленных по методу контурных токов.

Если в схеме некоторые узлы соединяются идеальными источниками э.д.с., то число t уравнений, составляемых по методу узловых потенциалов, уменьшается, t=n–m_и–1 (здесь m_и – число ветвей, содержащих только идеальные источники э.д.с.).

1.4.4. Метод двух узлов.

Этот метод наиболее рационален для расчета схем, содержащих два узла (для определенности узлы «a» и «b»). В данном методе за искомое принимают напряжение между двумя узлами, а затем с его помощью находят токи в ветвях схемы. Для таких схем узловое напряжение U_ab определяется формулой:

,

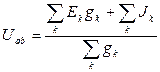где 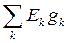 – алгебраическая сумма произведений э.д.с. ветвей (э.д.с. считаются положительными, если они направлены к узлу «a», и отрицательными, если направлены от узла «a» к узлу «b») на проводимости этих ветвей; J _k – токи источников тока (положительны, если они направлены к узлу «a», и отрицательны, если направлены от узла «a» к узлу «b»);  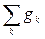– сумма проводимостей всех ветвей, соединяющих узлы «a» и «b».

1.4.5. Метод наложения.

Если в электрической цепи заданными величинами являются э.д.с. источников и токи источников тока, то расчет токов по методу наложения состоит в следующем. Ток в любой ветви можно рассчитать как алгебраическую сумму токов, вызываемых в ней э.д.с. каждого источника э.д.с. в отдельности и током, проходящим по этой же ветви от действия каждого источника тока (данный принцип справедлив для всех линейных электрических цепей). При этом надо иметь в виду, что когда ведется расчет токов, вызванных каким-либо одним источником э.д.с. или тока, то остальные источники э.д.с. в схеме заменяются короткозамкнутыми участками, а ветви с источниками тока остальных источников отключаются (ветви с источниками тока размыкаются). При этом для исходной схемы с общим числом источников э.д.с. и тока, равным n, получают и рассчитывают n частичных схем замещения, находя так называемые частичные токи. Истинные токи в ветвях находят путем алгебраического суммирования частичных токов данной ветви каждой из частичных схем. Методом наложения, однако, нельзя пользоваться для подсчета выделяемых в сопротивлениях мощностей как суммы мощностей от частичных токов (мощность является квадратичной функцией тока).

1.4.6. Методы преобразования.

Во всех случаях преобразования замена одних схем другими, им эквивалентными, не должна приводить к изменению токов или напряжений на участках цепи, не подвергшихся преобразованию.

Замена последовательно соединенных сопротивлений одним эквивалентным.

Сопротивления соединены последовательно, если они обтекаются одним и тем же током (рис. 1.3).

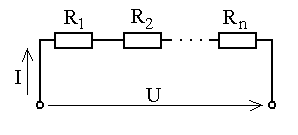
Рис. 1.3. Последовательное соединение сопротивлений

Эквивалентное сопротивление цепи, состоящей из n последовательно соединенных сопротивлений, равно алгебраической сумме этих сопротивлений:

.

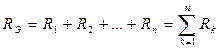При последовательном соединении n сопротивлений напряжения на них распределяются прямо пропорционально этим сопротивлениям:

U₁ : U₂ : . . . : U_n = R₁ : R₂ : . . . : R_n.

В частном случае двух последовательно соединенных сопротивлений:

U₁/U₂=R₁/R₂ ; U₁=UR₁/(R₁ + R₂) ; U₂=UR₂/(R₁ + R₂),

где U – общее напряжение, действующее на участке цепи, содержащем два сопротивления R₁ и R₂.