Основные понятия. Источники электрической энергии.

    Электрической цепью называют совокупность соединенных друг с другом источников электрической энергии и приемников (нагрузок), по которой может протекать электрический ток.

    Электрическим током называют упорядоченное движение заряженных частиц. Ток, неизменяющийся по величине и направлению, называют постоянным током.

    Электрической схемой называют изображение электрической цепи, выполненное с помощью принятых для этой цели условных графических обозначений.

Пассивный элемент электрической цепи – это элемент, не являющийся источником электромагнитной энергии (резистор с электрическим сопротивлением R).

Активный элемент электрической цепи – это элемент, являющийся источником электромагнитной энергии.

Ветвью электрической цепи называется участок цепи, вдоль которого ток имеет одно и то же самое значение.

Узлом электрической цепи называется точка соединения трех и более ветвей. На схемах узел обозначается точкой, наносимой в месте электрического соединения ветвей.

Контуром электрической цепи называется замкнутый путь, образованный одной или несколькими ветвями.

Вольт-амперная характеристика элемента электрической цепи – это зависимость тока, протекающего по элементу, от напряжения на зажимах этого элемента (или наоборот).

Элементы электрической цепи, имеющие вольт-амперные характеристики, изображаемые прямой линией, называют линейными элементами. Электрический цепи, составленные исключительно из линейных элементов, называют линейными электрическими цепями.

Источник электродвижущей силы.

Для идеального источника э.д.с. напряжение на его зажимах U_ab не зависит он величины протекающего через источник тока I и характеризуется его электродвижущей силой E (обозначения положительных направлений напряжения и тока показаны на рис. 1.1, а): U_ab=E. Внешняя характеристика такого источника изображена прямой 1 на рис. 1.2, а. Внутреннее сопротивление идеального источника э.д.с. равно нулю.

Реальный источник электродвижущей силы (рис. 1.1, б) обладает, в отличие от идеального, некоторым внутренним сопротивлением; он может быть изображен в виде последовательной схемы, содержащей э.д.с. E и сопротивление R. Внешняя характеристика такого источника изображена прямой 2 на рис. 1.2, а.

Источник тока.

Для идеального источника его ток J не зависит от напряжения U_ab, так как внутренняя проводимость источника тока равна нулю, напряжение источника тока бесконечно велико. Обозначения положительных направлений тока и напряжения показаны на рис. 1.1, в. Внешняя характеристика такого источника изображена прямой 1 на рис. 1.2, б.

Реальный источник тока (рис. 1.1, г) обладает, в отличие от идеального, некоторой внутренней проводимостью g=1/R; он может быть изображен в виде параллельной схемы, содержащей источник тока J, численно равный току короткого замыкания источника тока, и проводимость g. Внешняя характеристика такого источника изображена прямой 2 на рис. 1.2, б.

Переход от схемы источника электродвижущей силы к эквивалентной схеме источника тока осуществляется по формулам:

J=E/R, E=J/g, R=1/g.

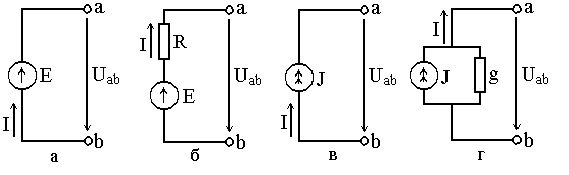
Рис. 1.1. Источники э.д.с. и тока

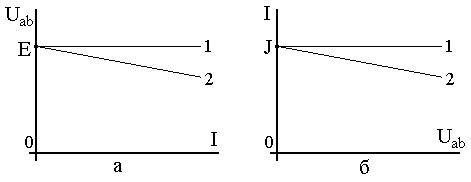
Рис. 1.2. Внешние характеристики источников э.д.с. и тока

Закон Ома.

Этот закон применяется для ветви или для одноконтурной замкнутой цепи (не имеющей разветвлений). Для записи выражения по закону Ома необходимо выбрать (произвольно) некоторое положительное направление тока.

Закон Ома для участка цепи, не содержащего источников э.д.с.

Для ветви, не содержащей источников э.д.с. и состоящей только из пассивных элементов (сопротивлений),

,

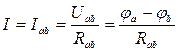где U_ab= j_a– j _b – разность потенциалов между зажимами « a» и « b» рассматриваемого участка, взятая по выбранному направлению тока; R_ab – суммарное сопротивление участка ab схемы.

Закон Ома для участка цепи, содержащего источники э.д.с.

Для участка цепи с э.д.с закон Ома имеет вид:

,

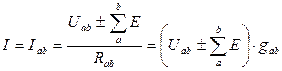где 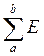 – алгебраическая сумма э.д.с., действующих на участке ab, причем каждая э.д.с., совпадающая по направлению с положительным направлением тока, записывается с положительным знаком, а несовпадающая – с отрицательным.

Необходимо помнить, что если в результате расчета тока получается отрицательная величина, то это значит, что действительное направление тока противоположно первоначально выбранному направлению.

Законы Кирхгофа.

Для записи выражений, составленных на основании законов Кирхгофа, необходимо задаться положительными направлениями токов каждой ветви.

Первый закон Кирхгофа применяется для описания состояния узлов электрической цепи. Он формулируется следующим образом: алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю,

.

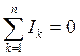Токи, отекающие от узла, условно принимаются положительными, а втекающие в него – отрицательными (или наоборот).

Второй закон Кирхгофа применяется для описания состояния замкнутых контуров. Он формулируется следующим образом: алгебраическая сумма э.д.с. замкнутого контура равна алгебраической сумме падений напряжений на всех элементах данного контура:

.

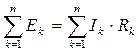Направление обхода контура выбирается произвольно. При записи левой части уравнения те э.д.с., направления которых совпадают с выбранным направлением обхода контура (независимо от направления тока, протекающего через них), принимаются положительными, а э.д.с., направленные против выбранного направления обхода – отрицательными. При записи правой части уравнения со знаком плюс берутся падения напряжения в тех ветвях, в которых выбранное положительное направление тока совпадает с направление обхода (независимо от направления э.д.с. в этих ветвях), а со знаком минус – падения напряжения в тех ветвях, в которых положительное направление тока противоположно направлению обхода.

Оба закона Кирхгофа являются следствиями закона сохранения энергии применительно к электрическим цепям.