2.1. Основные понятия и определения.

    Переменный ток – это ток, изменяющийся во времени по величине и направлению.

    В практической электротехнике в большинстве случаев переменные токи, напряжения и э.д.с. – это величины, изменяющиеся по синусоидальному закону (см. рис. 2.1).

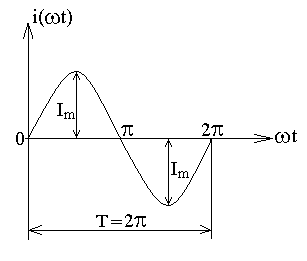
Рис. 2.1. Синусоидально изменяющийся ток

    Наименьший промежуток времени, через который периодически изменяющаяся величина повторяется по форме и величине, называется периодом Т.

    Значение синусоидально изменяющейся функции в любой момент времени (то есть ордината функции) называется мгновенным значением (соответственно, мгновенным значением тока, напряжения или э.д.с.).      

Мгновенное значение синусоидально изменяющейся величины может быть задано выражением вида:

a(t)=A_msin( w t + y )=A_msin [ w (t + ) ],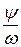

где A_m – максимальное значение, или амплитуда (I_m на рис. 2.1); wt+ y – фаза (фазовый угол); y – начальная фаза (начальный фазовый угол); y / w – начальный фазовый сдвиг; w – угловая частота.

Период Т, угловая частота w и частота f связаны соотношениями:

w = 2 p f = 2 p / T ; f = 1 / T .

    Понятия начальной фазы и сдвига по фазе проиллюстрируем рис. 2.2, на котором изображены два синусоидальных тока одинаковой частоты: i ₁ ( t )= I_{m 1} sin (ω t +ψ₁), i ₂ ( t )= I_{m 2} sin (ω t +ψ₂).

    Начальная фаза всегда отсчитывается в момент перехода кривой из отрицательной области в положительную в сторону начала координат (переход берут ближайший к началу координат). Знак начальной фазы определяют из сопоставления направления отсчета начальной фазы и положительного направления оси абсцисс: если они совпадают, знак начальной фазы положительный, в противном случае – отрицательный.

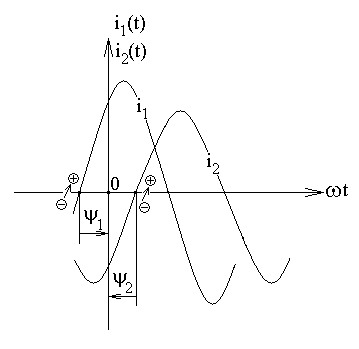
Рис. 2.2. К понятию начальной фазы

    Сдвиг по фазе двух синусоидальных функций одной частоты определяют как разность их начальных фаз: Δψ=ψ₁–ψ₂; причем если Δψ=(ψ₁– ψ₂)>0, то ток I₁ опережает ток I₂ по фазе, а если Δψ=(ψ₁– ψ₂)<0, то ток I₁ отстает от тока I₂ по фазе.

    Таким образом, если начала функций времени одной частоты не совпадают, то они сдвинуты по фазе, Δψ≠0. Если начала функций совпадают, то они синфазны, Δψ=0. Если начала функций времени сдвинуты на ±π (±180º), то они находятся в противофазе, Δψ=±π. Если начала функций времени сдвинуты на ±π/2, то они находятся в квадратуре, Δψ=±π/2.

Действующие значения переменных токов, напряжений, э.д.с. определяются как

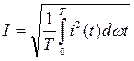
(для напряжения и э.д.с. структура выражений аналогична). Для синусоидально изменяющихся э.д.с., напряжения и тока

E=E_m/ 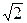=0,707E_m, U=U_m/ 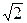, I=I_m/ .

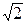Средние значения переменных токов, напряжений, э.д.с. за положительную полуволну определяются как

(для напряжения и э.д.с. структура выражений аналогична). Для синусоидально изменяющихся э.д.с., напряжения и тока

Е_ср=2 E _m / p =0,637Е_m, U_ср=2U_m/ p , I_ср=2I_m/ p.

Среднее значение синусоидально изменяющейся величины а(t)=A_msin( w t+ y ) за целый период равно нулю.

Изображение синусоидальной функции вращающимся вектором.

Проекция вращающегося против часовой стрелки с постоянной угловой скоростью w вектора 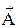_m на вертикальную ось изменяется во времени по синусоидальному закону: a(t)=A_msin( wt + y ), поэтому любая синусоидальная функция (ток, напряжение, э.д.с.) может быть изображена в виде вектора.