Выполните матричное умножение.
Z=1/(N-1)*ВT*В
Где N-об’ем выборки,Х и ХТ соответствующие матрицы.
Для этого выделим блок ячеек 4х4
И вставим в него формулу
Получим
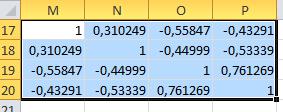
Матрица Z называется матрицей парных корреляций.
По главной диагонали Z находятся 1 ,а снизу и сверху коэффициенты корреляции. Докажите, что матрица Z положительно определенная.
Поверьте Ваши вычисления для исходной МСВ, используя АНАЛИЗ ДАННЫХ команды ковариация и корреляция.
Вычисление частного и множественного коэффициентов корреляции многофакторной случайной величины.
Вычислим определитель матрицы парных корреляций, используя функцию МОПРЕД и матрицу обратную к ней МОБР. Скопируйте значение определителя и с помощью специальной вставки вычислите присоединенную матрицу парных корреляций.
Частные коэффициенты корреляций характеризуют силу линейной связи между парами признаков без учета влияния других признаков в «чистом» виде и вычисляются по формуле
rij,k,l= -Аij/(Ai,iAj,j)1/2
где Аi,j,Ai,i,Aj,j соответствующие элементы присоединенной матрицы (алгебраические дополнениям элементов матрицы парных корреляций.)
Вычислим обратную матрицу к матрице парных корреляций(МОБР())
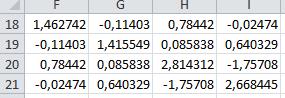
Присоединенная матрица(матрица алгебраических дополнений) получается умножением каждого элемента обратной матрицы на определитель матрицы парных корреляций.
Равный 0,204351(Мопред())
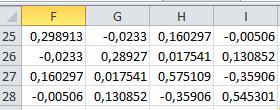
Вычислим Множественный коэффициент корреляции для элемента а11 матрицы парных корреляций
r211ij,k,=1-0,204351/0,298913=-0,316352
Для элемента а22
r2 22ij,k,l=1-D/D2=1-0,204351/0,28987=0,29356
Частный коэффициент корреляции для переменных Х1 и Х2
r2 12ij,k,l =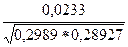 
=0,079
Самостоятельно вычислите r 2 13ij,k,l r 2 2,3ij,k,l r 2 24 ij,k,l
Самостоятельно Постройте матрицу парных корреляций для выборки и вычислите частные и множественные коэффициенты корреляции
| Рентабельность | фондоотдача | фондоворужонность. |
| 13,25 | 1,45 | 6,4 |
| 10,16 | 1,3 | 7,8 |
| 13,72 | 1,37 | 9,76 |
| 12,85 | 1,62 | 7,9 |
| 10,63 | 1,91 | 5,35 |
| 9,13 | 1,68 | 9,9 |
| 25,83 | 1,94 | 4,5 |
| 23,39 | 1,89 | 4,88 |
| 14,68 | 1,94 | 3,46 |
| 10,05 | 32,4 | 2,06 |
| 14 | 11,52 | 2 |
| 9,66 | 17,28 | 1,02 |
| 10,03 | 16,2 | 1,85 |
| 9,13 | 13,32 | 0,9 |
| 5,17 | 17,28 | 0,62 |
| 9,9 | 9,72 | 1,09 |
| 12,62 | 16,2 | 1,6 |
| 5,02 | 24,84 | 1,53 |
Лабораторная работа 7. Регрессионно-корреляционный анализ многофакторных выборок.
Формулировка задания.
Даны статистические данные наблюдений за некоторым количеством однотипных однородных экономических объектов требуется провести полный корреляционно регрессионный анализ.
Для этого.
-определить и оценить силу линейной связи между ними,
-построить и исследовать модель регрессии;
-построить графики регрессии и отклонений от нее
| Рент. | ненормир.Оборотные с-ва | фондоотдача | фондоворужонность. | нормир.обор.с-ва |
| 13,25 | 10,08 | 1,45 | 6,4 | 166,2 |
| 10,16 | 14,76 | 1,3 | 7,8 | 92,88 |
| 13,72 | 6,48 | 1,37 | 9,76 | 158,04 |
| 12,85 | 21,96 | 1,62 | 7,9 | 93,96 |
| 10,63 | 11,88 | 1,91 | 5,35 | 173,88 |
| 9,13 | 12,6 | 1,68 | 9,9 | 162,3 |
| 25,83 | 11,52 | 1,94 | 4,5 | 88,56 |
| 23,39 | 8,28 | 1,89 | 4,88 | 101,16 |
| 14,68 | 11,52 | 1,94 | 3,46 | 166,32 |
| 10,05 | 32,4 | 2,06 | 3,6 | 140,76 |
| 14 | 11,52 | 2 | 3,56 | 128,52 |
| 9,66 | 17,28 | 1,02 | 5,65 | 177,84 |
| 10,03 | 16,2 | 1,85 | 4,28 | 114,48 |
| 9,13 | 13,32 | 0,9 | 8,9 | 93,24 |
| 5,17 | 17,28 | 0,62 | 8,52 | 126,72 |
| 9,9 | 9,72 | 1,09 | 7,19 | 91,8 |
| 12,62 | 16,2 | 1,6 | 4,82 | 69,12 |
| 5,02 | 24,84 | 1,53 | 5,46 | 66,24 |
| 21,18 | 14,76 | 1,4 | 6,2 | 67,68 |
| 25,17 | 7,56 | 2,22 | 4,25 | 50,4 |
| 19,4 | 8,64 | 1,32 | 5,88 | 70,6 |
| 21 | 8,64 | 1,48 | 5,88 | 72 |
| 6,57 | 9 | 0,68 | 9,27 | 97,2 |
| 14,2 | 14,8 | 2,3 | 4,4 | 80,3 |
| 15,8 | 10,1 | 1,4 | 10,3 | 51,5 |
| 5,23 | 14,8 | 1,5 | 4,7 | 105,1 |
| 8 | 10,44 | 1,43 | 4,2 | 128,5 |
| 17,5 | 14,75 | 1,82 | 3,13 | 94,7 |
| 17,16 | 20,52 | 2,62 | 4 | 85,32 |
| 14,54 | 14,4 | 1,75 | 5,23 | 76,3 |
Выполнение работы.
1.Занесем данные в ячейки рабочего листа MS EXCEL.
2. Определим количественные характеристики связи, используя настройку
Анализ данных \корреляция.
| Рентабельность | ненормир.Оборотные с-ва | фондоотдача | фондоворуж. | нормир.обор.с-ва | |
| Рентабельность | 1 |
|
|
|
|
| Ненорм.Обор с-ва | -0,3735 | 1 |
|
|
|
| фондоотдача | 0,47878 | 0,192469 | 1 |
|
|
| фондоворуж. | -0,29462 | -0,241921 | -0,66241838 | 1 |
|
| Норм.обор.с-ва | -0,38508 | 0,021457 | -0,07516782 | 0,019524 | 1 |
3.Проверим значимость коэффициентов парных корреляций и вычислим их доверительные интервалы.
3.1. Проверка значимости
Вычислим величину
Тнабл=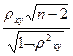 
Таблица Т расч , для каждого коэффициента корреляции
| 0 |
|
|
|
|
| -2,1308 | 0 |
|
|
|
| 2,8857 | 1,037856 | 0 |
|
|
| -1,6313 | -1,31932 | -4,6789 | 0 |
|
| -2,2079 | 0,113569 | -0,3988 | 0,103333 | 0 |
Т кр=2,048
Отсюда можем сделать вывод о значимости только 4 коэффициентов
Для вычисления интервальных оценок воспользуемся методикой предыдущей работы, раздел 4.2
Данные удобно представить таблицей.
| фишер | Zr | ΔZ | мин =Zr-Δ | мах=Zr+Δ |
| р,1 | -0,3925 | 0,328970 | -0,72149828 | -0,06356 |
| р,2 | 0,52140 |
| 0,1924356 | 0,85037 |
| р,4 | -0,4060 |
| -0,7349811 | -0,07704 |
| r 3,2 | -0,7971 |
| -1,1260814 | -0,46814 |
После выполнения обратных преобразований Фишера получим.
| гран.корел | ρl=F(мин) | ρh=F(мах) |
| р,1 | -0,617836 | -0,0634 |
| р,2 | 0,190094 | 0,69126 |
| р,4 | -0,626103 | -0,0768 |
| 3,2 | -0,809673 | -0,4367 |
4.Расчет частных коэффициентов корреляции.
Частные коэффициенты корреляции характеризуют силу линейной связи двух факторов, без учета влияния остальных
Р=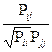 
, Р I,j алгебраическое дополнение соответствующего элемента матрицы парных корреляций.
Для вычисления их используем прием.
а) вычислим обратную матрицу матрицы парных корреляций
б) вычислим ее определитель
в) с помощью специальной вставки , выполним умножение элементов обратной матрицы на значение определителя.
а)Обратная матрица.
| 2,317 | 1,112 | -1,148 | 0,176 | 0,779 |
| 1,112 | 1,599 | -0,616 | 0,300 | 0,342 |
| -1,148 | -0,616 | 2,367 | 1,086 | -0,272 |
| 0,176 | 0,300 | 1,086 | 1,842 | 0,107 |
| 0,779 | 0,342 | -0,272 | 0,107 | 1,270 |
Определитель
0,2257
Матрица алгебраических дополнений
| 0,523 | 0,251 | -0,259 | 0,040 | 0,176 |
| 0,251 | 0,361 | -0,139 | 0,068 | 0,077 |
| -0,259 | -0,139 | 0,534 | 0,245 | -0,061 |
| 0,040 | 0,068 | 0,245 | 0,416 | 0,024 |
| 0,176 | 0,077 | -0,061 | 0,024 | 0,287 |
Теперь использованием формулы, для частных коэффициентов корреляции , вычислим их значение, но только для значимых коэффициентов.
| 0,5778 | 1,0000 |
|
|
| -0,4904 | -0,3166 | 1,0000 |
|
| 0,0851 |
| 0,5202 | 1,0000 |
| 0,4539 |
|
|
|
Оценим их значимость по тем же критериям
5. Построение модели регрессии
У-рентабельность
Протокол регрессии
| Регрессионная статистика | |
| Множественный R | 0,753923 |
| R-квадрат | 0,568400 |
|
|
|
|
|
|
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | 17,1885 | 6,7479 | 2,5472 | 0,0174 |
| ненормир.Оборотные с-ва | -0,5002 | 0,1413 | -3,5401 | 0,0016 |
| фондоотдача | 6,2535 | 2,2228 | 2,8133 | 0,0094 |
| фондоворуж. | -0,2059 | 0,4822 | -0,4269 | 0,6731 |
| нормир.обор.с-ва | -0,0513 | 0,0201 | -2,5470 | 0,0174 |
Из протокола видно, что модель работает на 75%
Имеет вид
У=17,18- 0,5Х1+6,25Х2-0,206Х3-0,05Х4
Все коэффициенты кроме третьего значимы.
Имеет место мультиколлинеарность, второй и третьей переменной, одну из них надо исключить из анализа
Новая модель.
| Множественный R | 0,75183 |
| R-квадрат | 0,56525 |
| Нормированный R-квадрат | 0,51509 |
| Стандартная ошибка | 4,03248 |
Дата: 2018-12-21, просмотров: 263.
