Важнейшим требованием к информации при использовании массовых данных является её качественная и количественная однородность.
Качественная однородность предполагает, что обследованию будут подвергаться наблюдения или объекты, схожие друг с другом. Использование разнородных объектов будет искажать характер связи между отдельными признаками.
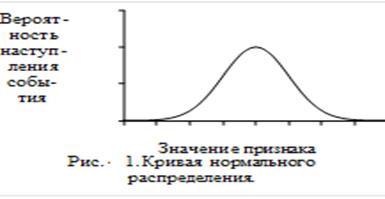
Для большинства экономических показателей характерно распределение данных, близкое к нормальному. Нормальным распределением называется такое, которое получается из ряда наблюдений, вариация которых обусловлена воздействием большого числа мелких беспорядочных или случайных влияний.
Кривая нормального распределения представлена на рис. 4.1. Как видно из рисунка, наиболее часто встречаются значения признака, близкие к его среднему. По мере удаления от среднего значения число наблюдений или вероятность наступления события уменьшаются. Причем в интервал от `х- s х до `х+ s х попадает 68,26% случаев; от `х-2s х до `х+2s х – 95,46%; от `х-3s х до `х+3s х – 99,73% случаев..
Эти теоретические положения, характеризующие кривую нормального распределения.
Исходная информация, которая будет использована для построения эконометрических моделей, должна быть достоверной. Для проверки информации на достоверность необходимо рассчитать и оценить 2 показателя: асимметрию(А) и эксцесс (Э). Эти показатели определяются по формулам:
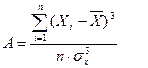
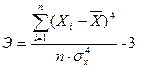
Xi – фактическое значение показателя;
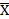 - среднее значение показателя;
- среднее значение показателя;
n – количество опытов;
σx – среднеквадратическое отклонение, которое, в свою очередь, рассчитывается по формуле:
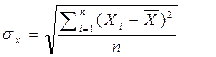
На примере информации о посещаемости студентами занятий и их успеваемости уточним методику расчета асимметрии и эксцесса.
Таблица – Посещаемость занятий студентами и их оценки на экзамене
| Номер | Пропуски | Оценка | Номер | Пропуски | Оценка |
| 1 | 1 | 8 | 14 | 1 | 5 |
| 2 | 4 | 5 | 15 | 4 | 3 |
| 3 | 3 | 4 | 16 | 3 | 7 |
| 4 | 0 | 7 | 17 | 2 | 5 |
| 5 | 2 | 7 | 18 | 0 | 7 |
| 6 | 6 | 2 | 19 | 1 | 9 |
| 7 | 5 | 1 | 20 | 5 | 6 |
| 8 | 1 | 10 | 21 | 3 | 5 |
| 9 | 0 | 9 | 22 | 2 | 7 |
| 10 | 7 | 3 | 23 | 3 | 3 |
| 11 | 4 | 5 | 24 | 2 | 8 |
| 12 | 3 | 4 | 25 | 0 | 10 |
| 13 | 2 | 6 |
Таблица 3– Порядок расчета асимметрии и эксцесса
| Номер | Xi | (Xi – 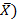
| (Xi – 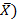 2 2
| (Xi – 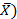 3 3
| (Xi – 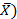 4 4
|
| 1 | 1 | -1,56 | 2,4336 | -3,7964 | 5,9224 |
| 2 | 4 | 1,44 | 2,0736 | 2,9860 | 4,2998 |
| 3 | 3 | 0,44 | 0,1936 | 0,0852 | 0,0375 |
| - | - | - | - | - | - |
| 25 | 0 | -2,56 | 6,5536 | -16,7772 | 42,9497 |
| Итого | 64 | Х | 88,16 | 83,5008 | 808,6177 |
| Среднее | 2,56 | Х | 3,5264 | 3,34 | 32,34 |
Таким образом,
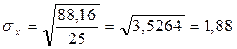

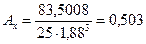
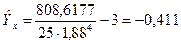
Если параметры А и Э равны нулю, то исходная информация в полной мере считается достоверной. Конечно, такой идеальный вариант при изучении экономических явлений и процессов встречается крайне редко. Чаще всего асимметрия и эксцесс не равны нулю.
Если асимметрия принимает положительное значение, то соответствующее поле вероятностей сдвигается вправо относительно графика нормального распределения (смотрите рисунок 1). Соответственно, отрицательный коэффициент асимметрии свидетельствует о перемещении графика влево.
Конкретное значение эксцесса отражает перемещение графика распределения вероятностей по вертикали. В частности, если поле вероятностей островершинное, то Э> 0. В свою очередь, уменьшение коэффициента Э приводит к тому, что изучаемый график становится все более пологим.
В связи с этим встает вопрос о возможных границах отклонений коэффициентов А и Э от нулевых значений. Информацию можно считать достоверной и пригодной для дальнейшей обработки, если выполняются следующие два неравенства:
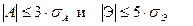
В приведенных формулах σА и σЭ представляют собой ошибки асимметрии и эксцесса, соответственно, которые определяются по формулам:
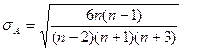
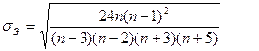
Нетрудно заметить, что ошибки асимметрии и эксцесса зависят только от числа опытов n. В нашем примере (n = 25) ошибка асимметрии составляет:
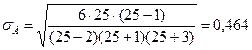
Что касается ошибки эксцесса, то при n=25 она равна:
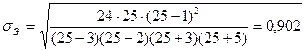
Так как асимметрия по факторному признаку меньше трех ошибок (0,503 ≤ 3∙ 0,464), а эксцесс по модулю ниже пяти соответствующих ошибок (0,411 ≤5∙0,902), то информацию о пропусках занятий следует считать достоверной.
Легко проверить, что асимметрия и эксцесс по результативному показателю также находятся в допустимых пределах (Ау = -0,055; Эу = -0,764).
На этапе проверки информации на достоверность рекомендуется удалить ту информацию, которая резко выделяется из изучаемой совокупности. Речь идет о слишком высоких или очень низких значениях показателей. Выход коэффициентов асимметрии и эксцесса за допустимые границы сигнализирует о том, что такие значения имеют место. Выделить эти ”нестандартные” значения позволяет правило трех сигм: |Xi - 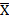 | ≤3∙σx. Соответственно, для результативного показателя данное правило может быть записано в виде: |Yi -
| ≤3∙σx. Соответственно, для результативного показателя данное правило может быть записано в виде: |Yi - 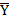 | ≤3∙σy.
| ≤3∙σy.
Рассмотрим пропуски занятий и применим правило трех сигм в отношении первых двух студентов:
|X1 - 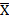 | = |-1,56 | ≤ 3∙1,88
| = |-1,56 | ≤ 3∙1,88
|X2 - 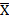 | = |1,44 | ≤ 3∙1,88.
| = |1,44 | ≤ 3∙1,88.
Расчеты показывают, что и по всем остальным студентам правило трех сигм соблюдается (в отношении факторного показателя).
Что касается оценок, т.е. результативного показателя, то и в этом случае модуль отклонения фактических значений от средней оценки не превышает трех сигм ( 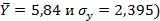 . Проверим это утверждение на примере оценок, полученными седьмым и восьмым студентами:
. Проверим это утверждение на примере оценок, полученными седьмым и восьмым студентами:
|Y7 - 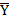 | = |1 – 5,84 | ≤ 3∙2,395
| = |1 – 5,84 | ≤ 3∙2,395
|Y8 - 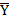 | = |10 – 5,84 | ≤ 3∙2,395.
| = |10 – 5,84 | ≤ 3∙2,395.
Вы заметили, что нами были взяты минимальная и максимальная оценки студентов. Если при этих значениях правило трех сигм соблюдается, то остальные значения можно не проверять.
Таким образом, исходная информация по всем студентам группы является достоверной. Это подтверждают коэффициенты асимметрии, эксцесса, а также правило трех сигм. Мы рекомендуем использовать правило трех сигм в любом случае, даже если асимметрия или эксцесс не выходят за допустимые границы. Это связано с тем, что в некоторых случаях нарушения асимметрии и эксцесса являются допустимыми, а правило трех сигм все равно не соблюдается.
Если какое-нибудь значение не удовлетворяет правилу трех сигм, то оно (значение) подлежит удалению. Одновременно следует удалить всю строку (опыт, объект, предприятие и т.д.), которой это значение принадлежит. Однако следует помнить, что удаляемая информация содержит, как правило, оригинальные и интересные факты. Именно поэтому, те объекты, которые мы должны удалить из изучаемой совокупности, требуется подвергнуть детальному монографическому анализу.
После удаления ”лишних” опытов целесообразно рассчитать новые значения асимметрии и эксцесса, а после этого убедиться в достоверности оставшейся части информации.
Задание. Используя данные нижеприведенной таблицы проверить все столбцы информации на достоверность
Таблица 1. – Информация для изучения объема продаж
| Номер наблюдения | Объем продаж, ед. | Цена реализации, ден. ед. | Затраты по стимулированию сбыта, ден. ед. | Количество торговых агентов, чел. |
| 1 | 120300 | 21,1 | 225600 | 2 |
| 2 | 90100 | 19,5 | 37400 | 1 |
| 3 | 112500 | 22,3 | 260500 | 4 |
| 4 | 109800 | 22,9 | 356800 | 5 |
| 5 | 97800 | 22,7 | 207000 | 3 |
| 6 | 118900 | 26,5 | 688700 | 3 |
| 7 | 84000 | 23,4 | 153500 | 2 |
| 8 | 70400 | 26,4 | 88700 | 2 |
| 9 | 99800 | 25,8 | 383200 | 8 |
| 10 | 89100 | 25,1 | 176700 | 2 |
| 11 | 72200 | 27,4 | 137600 | 2 |
| 12 | 97000 | 26,5 | 284400 | 4 |
| 13 | 108000 | 28,6 | 384600 | 5 |
| 14 | 69100 | 29,0 | 174000 | 2 |
| 15 | 95200 | 27,9 | 353300 | 5 |
| 16 | 86000 | 28,5 | 286200 | 4 |
| 17 | 61300 | 29,1 | 176100 | 3 |
| 18 | 71300 | 32,1 | 251700 | 3 |
| 19 | 66500 | 27,7 | 231900 | 4 |
| 20 | 92300 | 30,2 | 415400 | 4 |
| 21 | 82300 | 33,1 | 376000 | 5 |
| 22 | 73300 | 33,2 | 323600 | 4 |
| 23 | 52800 | 29,9 | 218600 | 3 |
| 24 | 97400 | 31,1 | 697800 | 6 |
| 25 | 69400 | 30,6 | 340700 | 4 |
| 26 | 41300 | 35,2 | 230100 | 3 |
| 27 | 63900 | 35,9 | 496800 | 5 |
| 28 | 81700 | 27,0 | 271000 | 3 |
| 29 | 96900 | 23,7 | 313000 | 3 |
| 30 | 72200 | 28,6 | 214400 | 3 |
| 35 | 89900 | 30,2 | 676200 | 7 |
Дата: 2018-12-21, просмотров: 403.