Вычислим величину
Тнабл= 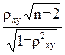
Т набл= -10,845
Для вычисления критического значения Используя функцию СТЬЮДРАСПОБР, категория статистические ,по заданному уровню значимости α=0,05 и числу степеней свободы (n-2)=10 определяют критическую точку tα/2 , n-2. Если модуль Т меньше tα/2 , n-2
С вероятностью 5% и степенями свободы 14 критическое значение распределения Стьюдента равно Ткр = 2,145
|Т набл| > Ткр , что свидетельствует о его значимости коэффициента корреляции
Рассчитаем д доверительные интервалы коэффициента корреляции
а)Выполним преобразование Фишера над коэффициентом корреляции, Фишер(ρ)
Ф(ρ)= -1,79078
б) вычислим отклонение ΔZ = 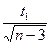 , где t1 значение функции Лапласа, встроенная функция НОРМСТОБР. t1=1.6448
, где t1 значение функции Лапласа, встроенная функция НОРМСТОБР. t1=1.6448
Величина отклонения с вероятностью 95% ΔZ= 0.4562
в) Предельные значения интервала в пространстве Фишера
А= -1,337-0,548=-2.2468
В=-1,337+0,548=-1.334
г) Обратное преобразование Фишера даст значения границ доверительного интервала для ρ вероятностью 95% -0,87 и -0,97
Самостоятельно рассчитайте силу связи между факторами таблицы.
| фондоотдача в мил.руб | фондоворужонность. в мил руб |
| 1,45 | 6,4 |
| 1,3 | 7,8 |
| 1,37 | 9,76 |
| 1,62 | 7,9 |
| 1,91 | 5,35 |
| 1,68 | 9,9 |
| 1,94 | 4,5 |
| 1,89 | 4,88 |
| 1,94 | 3,46 |
| 2,06 | 3,6 |
| 2 | 3,56 |
| 1,02 | 5,65 |
| 1,85 | 4,28 |
| 0,9 | 8,9 |
| 0,62 | 8,52 |
| 1,09 | 7,19 |
| 1,6 | 4,82 |
| 1,53 | 5,46 |
| 1,4 | 6,2 |
Корреляционный анализ в слабых шкалах
Коэффициенты ассоциации и контингенции. Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации и контингенции. Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т. е. состоящим из двух качественно отличных друг от друга значений признака (например, изделие годное или бракованное):
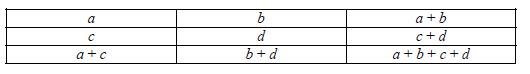
В этой таблице a, b, c, d являются частотами. Коэффициенты вычисляются по формулам:
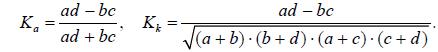
Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если или Ка≥0.5 Kk≥0.3
Пример. Исследуем связь между успеваемостью студентов и обеспеченностью учебно-методической литературой /Результаты обследования характеризуются следующими данными (человек):
| Группы студентов | Успевают | Не успевают | Итого |
| Обеспечены литературой | 42 | 7 | 49 |
| Не обеспечены литературой | 15 | 11 | 26 |
| Всего | 57 | 18 | 75 |
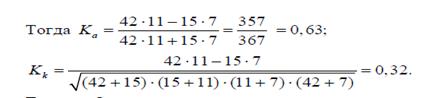
Сделайте вывод.
Самостоятельно выполните исследование.
На предприятии Х проводился социологический опрос удовлетворенности своей работой. Получены данные.
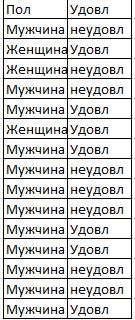
Рассчитать коэффициенты ассоциации и контингенции.
Примечание : при заполнении таблицы используйте функцию СчетЕсли()
Ранговые коэффициенты связи. В анализе социально-экономических явлений часто приходится прибегать к различным условным оценкам с помощью рангов, а взаимосвязь между отдельными признаками измерять с помощью непараметрических коэффициентов связи.
Ранжирование — это процедура упорядочивания объектов изучения, которая выполняется на основе предпочтения.
Ранг — порядковый номер значений признака, расположенных в порядке возрастания или убывания величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех значений принимается равным средней арифметической из соответствующих номеров мест, которые они занимают. Данные ранги называются связными.
Среди непараметрических методов оценки тесноты связи наибольшее значение имеют ранговые коэффициенты Спирмена и Кендэла. Эти коэффициенты могут быть использованы для определения тесноты связи как между количественными, так и между качественными признаками. Коэффициент корреляции Спирмена
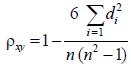
di квадраты разности рангов,n число наблюдений.
Если среди значений признаков х и у встречается несколько одинаковых, образуются связанные ранги, т. е. одинаковые средние номера; например, вместо одинаковых по порядку третьего и четвертого значений признака будут два ранга по 3,5. В таком случае коэффициент Спирмена вычисляется как:
где
j - номера связок по порядку для признака х;
Аj - число одинаковых рангов в j-й связке по х;
k - номера связок по порядку для признака у;
Вk - число одинаковых рангов в k-й связке по у.
Для проверки значимости коэффициента корреляции Спирмена используют те же методы, что и для коэффициента корреляции количественной шкалы.
Выполнение работы
Рассмотрим данные таблицы 1 Посещаемость занятий студентами и их оценки на экзамене (лабораторной работы 2), фрагмент исходной Excel таблицы.
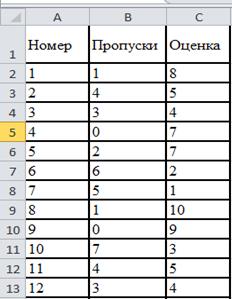
Выполним ранжирование рядов данных.(фрагмент таблицы ранжирование рядов),используя функцию

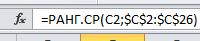
Обратите внимание, что вторым аргументом функции является массив , имеющих абсолютные адреса ячеек
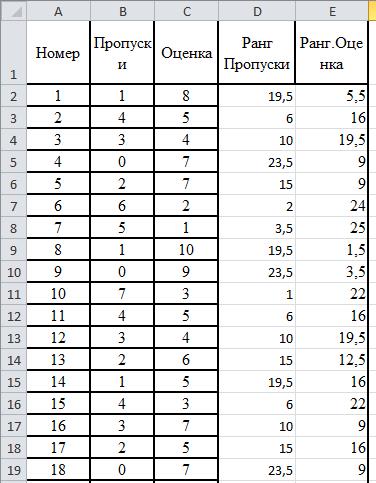
Вычислим разности рангов и квадраты разностей
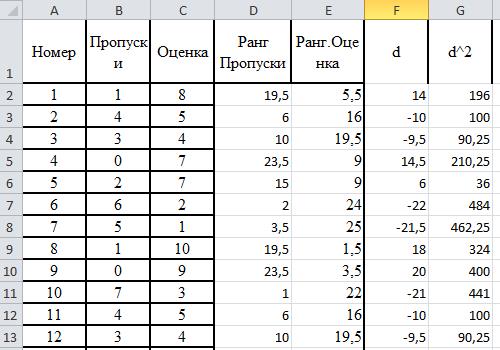
Подсчитаем сумму квадратов рангов
S=4548
Так как среди данных встречаются повторения, то для расчета коэффициента корреляции Спирмена , используем формулу
, где ,
j - номера связок по порядку для признака х;
Аj - число одинаковых рангов в j-й связке по х;
k - номера связок по порядку для признака у;
Вk - число одинаковых рангов в k-й связке по у.
Для подсчета одинаковых рангов по связкам, целесообразно скопировать в отдельную часть листа столбцы рангов и выполнить сортировки.
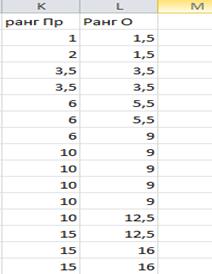
Из отсортированных данных видно, что повторяются 6 наблюдений с рангами
3,5 ; 6; 10; 15; 19,; 23,5
аналогично по оценкам одинаковые ранги у 8 наблюдений-это ранги
1,5 ; 3,5 ; 5,5 ;9 ; 12,5 ;16 ,19,5 22
, таким образом
Число рангов по связке Пропуск равно 6 , число рангов по связке оценка 8
Тогда
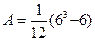 =17,5
=17,5
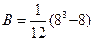 =42
=42
Число наблюдений-25
Тогда коэффициент корреляции Спирмена равен -0,767

Подсчитаем значимость
Тнабл= 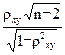 =5,73
=5,73
Ткр=1,73
Вывод коэффициент корреляции значим.
Самостоятельно рассчитать доверительный интервал.
Дата: 2018-12-21, просмотров: 467.