Корреляционный анализ имеет своей задачей количественное определение тесноты и направления связи между двумя признаками при парной связи и между результативным и множеством факторных признаков при многофакторной связи.
Корреляционная зависимость — это зависимость случайных величин (признаков), при которой изменению среднего значения одной соответствует изменение среднего значения другой случайной величины.
Показатели тесноты связи между признаками называют коэффициентами корреляции. Знаки при коэффициентах корреляции характеризуют направление связи между признаками.
В эконометрическом анализе используют числовые шкалы
1) номинальная шкала (наименований) предназначена для описания принадлежности объектов к определенным социальным группам;
2) шкала порядка (ранговая) применяется для измерения упорядоченности объектов по одному или нескольким признакам;
3) количественная шкала используется для описания количественных показателей.
Корреляционный анализ на количественной шкале.
Линейный коэффициент корреляции характеризует тесноту и направление связи между двумя коррелируемыми при-знаками в случае наличия между ними линейной зависимости. Расчет линейного коэффициента корреляции осуществляется по формуле
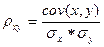, где cov(x,y)= 
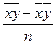ковариация двух факторов х и у, а σх ,σу стандартные отклонения этих факторов.
Значимость линейного коэффициента корреляции определяется с помощью t-критерия Стьюдента, сравнением величины с критическим значением tα/2 , n-2 с уровнем доверия α и числом степеней свободы выборки (n-2)
Тнабл=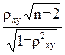 
Для вычисления критического значения tα/2 , n-2 Используя функцию СТЬЮДРАСПОБР, категория статистические ,по заданному уровню доверия α=0,05. Если модуль Тнабл меньше tα/2 , n-2 , то коэффициент корреляции значим. Доверительный интервал для коэффициента корреляции определяется по формулам:
,
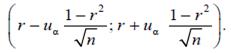где — uα критическая точка стандартного нормального распределения , соответствующего уровню значимости α и n— объем выборки.
Задача.. Предприятие розничной торговли исследуя влияние спроса на товары в зависимости от его цены составило выборку. Определить существует ли зависимость между этими данными
| № | цена товара | спрос на товар | № | цена товара | спрос на товар |
| 1 | 220 | 3,7 | 9 | 267 | 2,5 |
| 2 | 115 | 7,2 | 10 | 202 | 3,8 |
| 3 | 105 | 8,6 | 11 | 176 | 4,4 |
| 4 | 180 | 4,3 | 12 | 248 | 3,1 |
| 5 | 265 | 2,8 | 13 | 229 | 3,3 |
| 6 | 304 | 2,1 | 14 | 237 | 3,1 |
| 7 | 245 | 3,1 | 15 | 176 | 4,4 |
| 8 | 250 | 2,9 | 16 | 182 | 4,8 |
Выполнение работы.
1.Занесем данные в ячейки рабочего листа MS EXCEL
2. Заполним столбец Х*У, подсчитаем средние значения и стандартные отклонения используя функции среднее() , стандотглонГ()
.
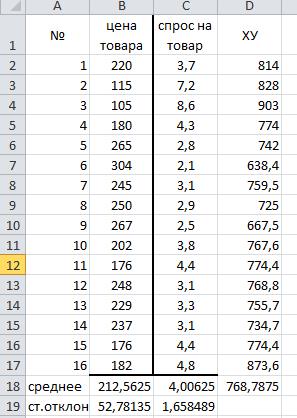
Подсчитаем ковариацию признаков, используя формулу
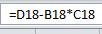
и корреляцию
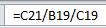
Результат
Коэффициент корреляции равен -0,945. Значение свидетельствует о сильной обратной связи переменных.
4.Проверим его значимость и вычислим доверительный интервал.
Дата: 2018-12-21, просмотров: 247.
