Самостоятельно Рассчитать коэффициент корреляции Спирмена по данным таблицы.
| год | объем реализации |
| 1979 | 105 |
| 1980 | 111 |
| 1981 | 110 |
| 1982 | 106 |
| 1983 | 118 |
| 1984 | 124 |
| 1985 | 113 |
| 1986 | 92 |
| 1987 | 91 |
| 1988 | 109 |
| 1989 | 113 |
| 1990 | 100 |
| 1991 | 94 |
| 1992 | 91 |
| 1993 | 92 |
| 1994 | 102 |
| 1995 | 106 |
Лабораторная работа 5. Регрессионно-корреляционный анализ двухфакторных выборок
Формулировка задания.
Даны статистические данные наблюдений за некоторым количеством однотипных однородных экономических объектов требуется провести полный корреляционно регрессионный анализ.
Для этого.
-построить график корреляционного поля;
-определить и оценить силу линейной связи между ними,
-построить и исследовать модель регрессии;
-построить графики регрессии и отклонений от нее.
Исходные данные.
| Объем производства (Х) | Себестоимость продукции (У) |
| 2,5 | 7,9 |
| 3,2 | 10,4 |
| 4,1 | 7,3 |
| 4,2 | 6,6 |
| 5,5 | 5,2 |
| 6,7 | 5,3 |
| 6,6 | 4,4 |
| 6,3 | 2,8 |
| 7,4 | 3,7 |
| 8,1 | 4,8 |
| 9,2 | 3,3 |
| 10 | 1,8 |
Выполнение работы.
1.Занесем данные в ячейки рабочего листа MS EXCEL.
2. Построим график корреляционного поля, используя диаграмму Точечная , данные оси ОХ Объем производства.
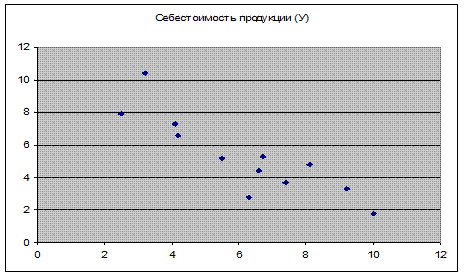
Из графика можно предположить о наличии линейной связи данных.
3. Определим количественные характеристики связи, используя настройку
Анализ данных \корреляция.
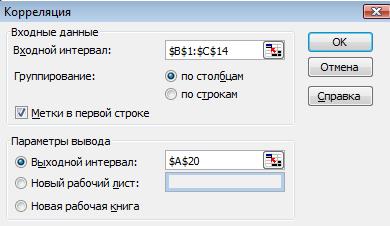
Результат
| Объем производства | Себестоимость продукции (У) | |
| Объем производства | 1 |
|
| Себестоимость продукции (У) | -0,871020552 | 1 |
Коэффициент корреляции равен -0,87. Значение свидетельствует о сильной связи данных.
4.Проверим его значимость и вычислим доверительный интервал.
4.1. Проверка значимости
Вычислим величину
Тнабл= 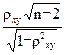
Т набл= -5,015033743
Для вычисления критического значения Используя функцию СТЬЮДРАСПОБР, категория статистические ,по заданному уровню значимости α=0,05 и числу степеней свободы (n-2)=10 определяют критическую точку tα/2 , n-2. Если модуль Т меньше tα/2 , n-2
С вероятностью 5% и степенями свободы 10 критическое значение распределения Стьюдента равно Ткр = 2,228139
|Т набл| > Ткр , что свидетельствует о его значимости коэффициента корреляции
4.2. .Рассчитаем д доверительные интервалы коэффициента корреляции
а)Выполним преобразование Фишера над коэффициентом корреляции, Фишер(ρ)
Ф(ρ)= - 1,337
б) вычислим отклонение ΔZ = 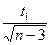 , где t1 значение функции Лапласа, встроенная функция НОРМСТОБР.
, где t1 значение функции Лапласа, встроенная функция НОРМСТОБР.
Величина отклонения с вероятностью 95% ΔZ= 0,548
в) Предельные значения интервала в пространстве Фишера
А= -1,337-0,548=-1,885
В=-1,337+0,548=-0,789
г) Обратное преобразование Фишера даст значения границ доверительного интервала для ρ вероятностью 95% -0,958 и -0,658
.5. Построим уравнение регрессии используя Анализ данных \ Регрессия.
Протокол Регрессионного анализа.
| Регрессионная статистика | |
| Множественный R | 0,871020552 |
| R-квадрат | 0,758676802 |
| Нормированный R-квадрат | 0,734544482 |
| Стандартная ошибка | 1,24847364 |
| Коэффициенты | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 10,82788711 | 10,3015 | 1,2099E-06 | 8,48589 | 13,16988 |
| Объем производства | -0,900198446 | -5,6069 | 0,000225 | -1,25792 | -0,54247 |
6.Оценки значимости.
6.1 Модель работает на 87%
 Коэффициент детерминации Множественный R= 0.76
Коэффициент детерминации Множественный R= 0.76
Уравнение регрессии У= 10,82- 0,9*Х
6.2. Оценки значимости коэффициентов
а) По критерию Стьюдента, необходимо сравнить данные Т статистики с критическим значением Стьюдента, найденным в пункте 4.1.
Для первого коэффициента 10,3015 >2,228139 для второго 5,6069>2,228139 , что свидетельствует о их значимости
б) оценка по Р значению.
Если величина в столбце Р значение меньше 0,05, то с вероятностью 0,95 соответствующий коэффициент значим.
в) доверительные интервалы для значимых коэффициентов регрессии
8.4886<10.827<13.17
-1.258<-0.9 <-0.542
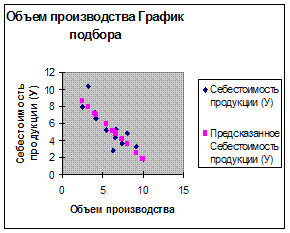
7. График подбора регрессии
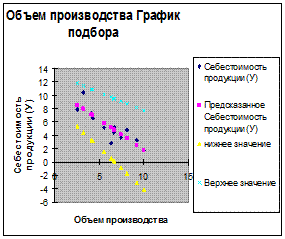
Изобразим на графике граничные линии регрессий доверительного интервала.
Для этого используем формулы
У=-0,542 х+13,69
У=-1,258Х+8,486
Подсчитаем среднюю себестоимость продукции, если объем производства составит 5т.у.е. У= -0,9*5+10,82=-4.5+10.82=6.32
Определим степень доверия
У=-0,542*5+13,69=10,98
У=-1,258*5+8,486=2,196
С вероятностью 95% Себестоимость будет в пределах(2,196;10,98) и в среднем 6,32
Какой будет объем производства, если себестоимость равна 2,5
Х=-(2,5-10,82) / 0,9=9,24
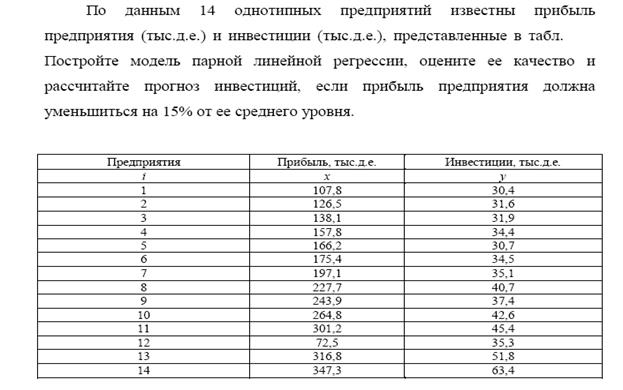
Самостоятельно провести анализ данных из таблиц и построить модель
Дата: 2018-12-21, просмотров: 324.