150
200
500
1000
2000
5000
1
76
80,5
76
78,6
79,55
78,32
2
82
79,5
79,6
78,8
78,85
79,26
3
86
81,5
76,6
77,6
79,1
77,22
4
75
82
78,8
80
79,55
79,34
5
77
72
76,2
79,8
79,4
79,22
6
81
77,5
76,6
77,6
77,4
77,44
7
75
81,5
80,4
78,5
78,1
79,28
8
74
76,5
81,8
79,7
77,2
78,82
9
71
80,5
76,6
76,4
77,76
78,74
10
84
72
81,2
78
78,4
77,74
Среднее
78,1
78,35
78,38
78,5
78,531
78,538
Дисперсия
23,65556
14,28056
5,035111
1,306667
0,789499
0,658618
Расчетное значение
78,54
В таблице приведены результаты эксперимента, исходя из которых можно сделать следующие заключения.
1. С ростом числа генерируемых точек (т. е. продолжительности прогона модели) оценки площади круга приближаются к точному значению (78,54 см2). На рис. 2 показаны оценки площади прогонов 1 и 2 в зависимости от продолжительности прогона п. Мы видим, что сначала оценки колеблются около точного значения, а затем стабилизируются. Это условие обычно достигается после повторения эксперимента достаточное количество раз. Наблюдаемое явление типично для результатов любой имитационной модели. Обычно в большинстве имитационных моделей нас интересуют результаты, полученные в стационарных условиях.
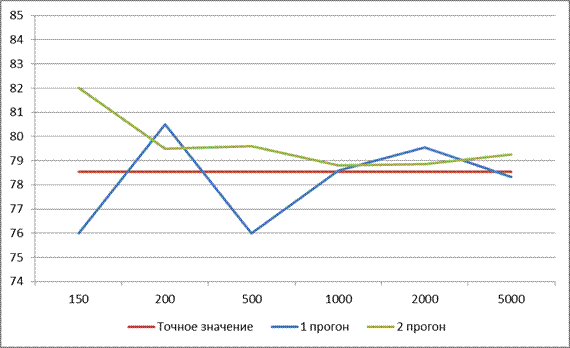
Рис. 2
2. Влияние переходных условий уменьшается, если усреднить результаты 10 серий. Это иллюстрирует рис. 3, на котором показана зависимость среднего от п. Кроме того, на рисунках видно, что для каждого п при достижении стационарных условий дисперсия убывает. При возрастании п от 150 до 200 дисперсия резко уменьшается с 23,66 до 14,25. За исключением этого интервала, столь резкого уменьшения дисперсии нигде больше не наблюдается. Последнее замечание указывает на то, что существует предел, за которым увеличение продолжительности прогона модели уже не дает существенного повышения точности результата, измеряемой дисперсией. Это замечание представляется чрезвычайно важным, поскольку затраты на эксплуатацию имитационной модели прямо пропорциональны продолжительности прогонов. Поэтому желательно найти компромисс между большой точностью (т. е. малой дисперсией) и небольшими затратами на процедуру получения результатов.
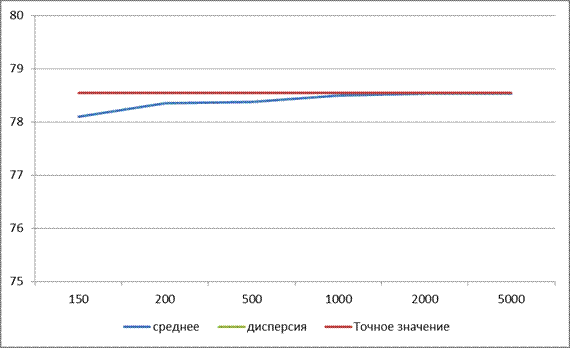
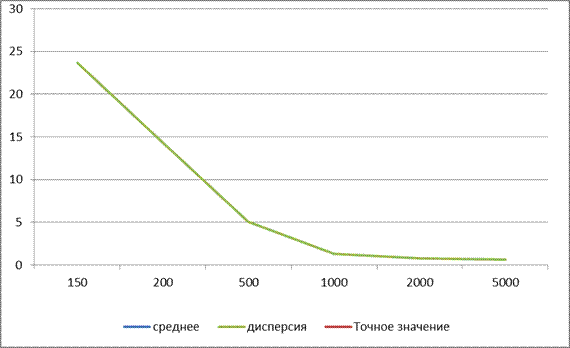
Рис.3.
3. Ввиду того что оценки площади имеют разброс, важно, чтобы результаты эксперимента, связанного с моделированием, были выражены в виде доверительных интервалов, показывающих величину отклонения от точного значений. В рассматриваемом примере, если А представляет собой точное значение площади, а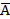 
и s2 — среднее и дисперсию N наблюдений, то 100 (1—α)%-ный доверительный интервал для А задается как
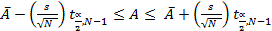
Задание (по вариантам)
1. Найти площадь фигуры, ограниченной линиями:
y=sin(x)+2
y=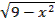 
y=0
2. Найти площадь фигуры, ограниченной линиями:
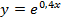
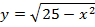
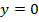
3. Найти площадь фигуры, ограниченной линиями:
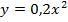
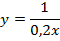
x=0
y=4
4. Найти площадь фигуры, ограниченной линиями:
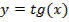
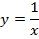
y=0
x=3
ЛАБОРАТОРНАЯ РАБОТА № 3
Тема. Моделирование временных характеристик
динамической системы с прямыми связями (2 часа)
Вопросы текущего контроля знаний
1. Дайте определение передаточной функции.
2. Поясните назначение элементов структурных схем: функционального блока; узла; сумматора.
Исходные данные
Замкнутая линейная динамическая система, состоящая из двух параллельных колебательных звеньев, описывается следующей системой уравнений:
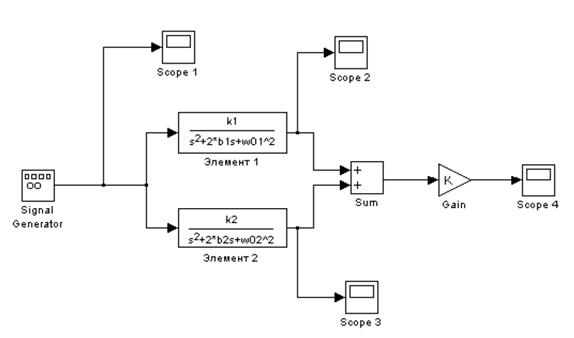
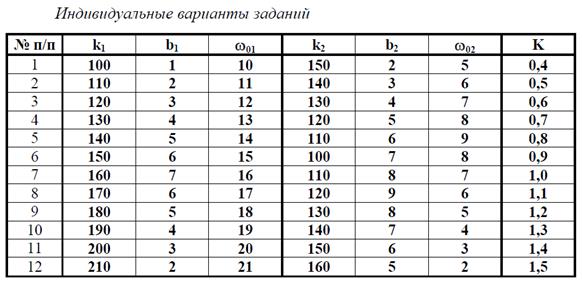
ЛАБОРАТОРНАЯ РАБОТА № 4
Тема. Моделирование временных характеристик
динамической системы с обратной связью (2 часа)
Вопросы текущего контроля знаний
3. Раскройте понятие обратной связи.
4. Дайте определение передаточной функции системы по рассогласованию.
Исходные данные
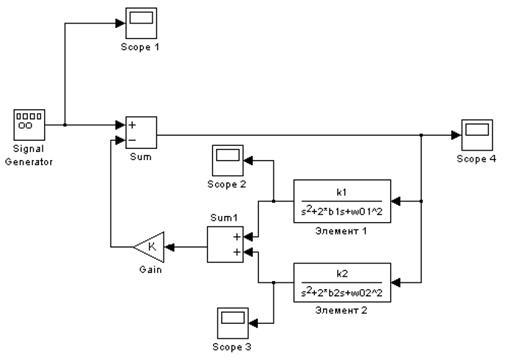
Замкнутая линейная динамическая система с отрицательной обратной связью, состоящая из двух параллельных колебательных звеньев, описывается следующей системой уравнений:
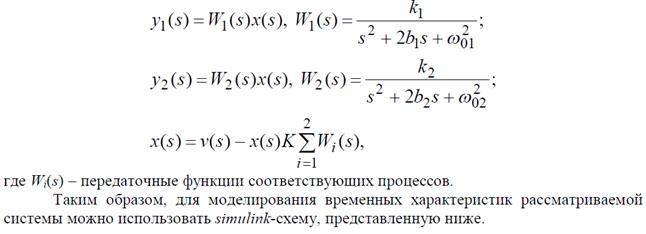
ЛАБОРАТОРНАЯ РАБОТА № 5
Тема. Моделирование временных характеристик динамической системы с перекрестными обратными связями (2 часа)
Вопросы текущего контроля знаний
1. Поясните принципиальные отличия классического и системного подходов.
2. Раскройте понятие перекрестной связи.
Исходные данные
Замкнутая линейная динамическая система с перекрестными обратными связями, состоящая из двух параллельных колебательных звеньев, описывается следующей системой уравнений:
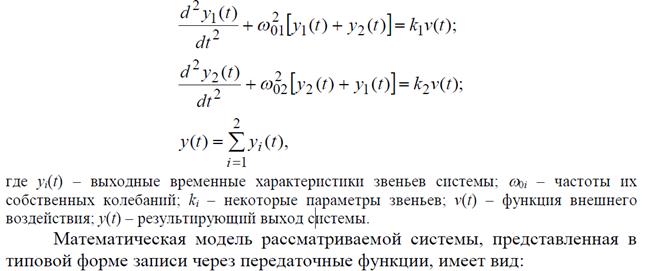
ЛАБОРАТОРНАЯ РАБОТА № 6
Тема. Комплексное моделирование характеристик
динамической системы с прямыми связями (2 часа)
Вопросы текущего контроля знаний
1. Раскройте понятие «математическое моделирование».
2. Поясните сущности вещественной и мнимой частотных характеристик системы.
Исходные данные
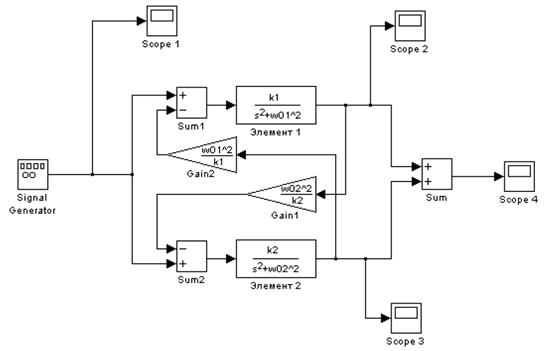
Математическая модель замкнутой линейной динамической системы, состоящей из двух параллельных колебательных звеньев, представленная в типовой форме записи через передаточные функции, имеет вид:
Цель работы
Целью лабораторной работы является изучение устройства, принципа работы и математических моделей электрических, гидравлических и пневматических рулевых приводов, а также анализ статической и динамических характеристик типового рулевого привода с помощью математической модели привода, составленной в системе программирования Матлаб.
Задание
При выполнение работы необходимо:
1. Изучить устройство, принцип работы и математические модели электрических, гидравлических и пневматических рулевых приводов (РП).
2. Для заданного варианта типового РП рассчитать и построить статическую характеристику привода при линейной и нелинейной моделях РП. Сравнить решения для линейной и нелинейной моделей.
3. Используя линейную модель РП, рассчитать экспериментально три значения логарифмических амплитудной и фазовой частотных характеристик (ЛАЧХ и ЛФЧХ) замкнутого РП при трех заданных значениях частоты гармонического входного сигнала.
4. С помощью блока LTI view Matlab рассчитать и построить графики ЛАЧХ и ЛФЧХ замкнутого РП.
5. Нанести значения ЛАЧХ и ЛФЧХ, рассчитанные в п.4. Сравнить экспериментальное и теоретическое решения.
6. Используя модели, рассчитать и построить переходные процессы на выходе линейной и нелинейной моделей РП при подаче на вход моделей ступенчатого воздействия. Сравнить решения для линейной и нелинейной моделей РП.
Порядок выполнения работы
Лабораторная работа выполняется бригадами на компьютерах.
Бригада выполняет вариант задания, выдаваемый преподавателем. Варианты различаются исходными данными для проведения расчетов.
Все расчеты проводятся в системе программирования Matlab с использованием пакета визуального программирования Simulink.
Предполагается, что начальные навыки работы в Matlab и Simulink были получены студентами при выполнении первой лабораторной работы по данной дисциплине.
Требуется:
1. Рассчитать и построить статические характеристики рулевого привода при линейной и нелинейной моделях привода. Сравнить и объяснить полученные решения.
2. Определить экспериментально путем проведения компьютерного эксперимента с моделью привода значения логарифмических амплитудной и фазовой частотных характеристик замкнутого рулевого привода при трех значениях частоты гармонического входного сигнала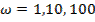 
рад/сек.
3. Рассчитать и построить логарифмические характеристики привода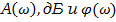 
, град. С помощью блока LTI view. Сравнить значения характеристик, полученные в п.2 экспериментально полученные значения.
4. Рассчитать и построить переходные процессы в приводе при нелинейной и линейной моделях привода.
Методика выполнения работы
Создание модели привода
Предварительно должны быть выполнены следующие действия:
1. Запустить MATLAB
2. Открыть приложение Simulink.
3. Создать программу моделирования линейного и нелинейного РП, показанную на рисунке.
Дата: 2018-12-21, просмотров: 653.
