MATLAB в режиме прямых вычислений

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Лабораторная работа №1

«Ознакомление с вычислительной системой MATLAB и ее использование для моделирования систем»

Цель лабораторной работы

Целью работы является изучение основных возможностей пакета MatLab, а также получение практических навыков работы с матрицами и средствами графической визуализации вычислений.

Описание системы MATLAB

1.2.1 Краткая характеристика MATLAB

MATLAB - это высокопроизводительный инструмент для выполнения технических расчетов. Он включает в себя вычисления, визуализацию и программирование в удобной среде, где задачи и решения выражаются в форме, близкой к математической. Типичное использование MATLAB - это:

§ математические вычисления

§ создание алгоритмов

§ моделирование

§ анализ данных, исследования и визуализация

§ научная и инженерная графика

§ разработка приложений, включая создание графического интерфейса

Рабочая среда MATLAB содержит следующие элементы:

§ меню;

§ панель инструментов с кнопками и раскрывающимся списком;

§ окно с вкладками Launch Pad и Workspace, из которого можно получить простой доступ к различным дополнительным модулям Toolbox и к содержимому рабочей среды;

§ окно с вкладками Command History и Current Directory, предназначенное для просмотра и повторного вызова ранее введенных команд, а также для установки текущего каталога;

§ командное окно Command Window;

§ строку состояния.

Настройка окон рабочей среды производится с помощью меню View и View -> Desktop Layout

Дополнительные возможности MATLAB

В MATLAB важная роль отводится специализированным группам программ, называемым toolboxes . Toolboxes – это всесторонняя коллекция функций MATLAB, которые позволяют решать частные технические задачи. Toolboxes применяются для обработки сигналов, анализа изображений, моделирования систем управления и т.д.

Для удобства работы в состав MATLAB входит программа Simulink, которая позволяет выполнять моделирование систем в графическом виде. Simulink содержит библиотеку элементов (blocksets) для построения систем из отдельных блоков и позволяет соединять эти блоки друг с другом с помощью мыши.

MATLAB в режиме прямых вычислений

Работа с системой в режиме прямых вычислений носит диалоговый характер и происходит по правилу «задал вопрос – получил ответ». Пользователь набирает на клавиатуре вычисляемое выражение, редактирует его (если нужно) в командном окне и завершает ввод нажатием клавиши ENTER.

Примеры:[1]

>>1+2

ans=3

>>ans/10

ans=0.08415

>>4*5; %(для блокировки вывода результата вычислений добавьте символ ";" (без кавычек) %в конец выражения)

>>sin(1)

ans=0.8415

Замечание:

ü Когда выходная переменная не определена, MATLAB использует переменную ans , коротко от answer - ответ, для хранения результатов вычисления.

ü Если вводимое математическое выражение окажется настолько длинным, что на него не хватит одной строки, то часть выражения можно перенести на новую строку с помощью знака многоточия «…» (3 или более точек).

ü Текстовый комментарий к выполняемым действиям в MATLAB можно ввести после знака %.

Операторы

Простейшие алгебраические:

+ сложение

- вычитание

* умножение

/, \ деление

^ степень

' комплексно сопряженное транспонирование

() определение порядка вычисления

Отношения:

< - меньше

> - больше

<= - меньше или равно

>= - больше или равно

== - равно

~= - не равно

Функции

MATLAB предоставляет большое количество элементарных математических функций, таких как abs, sqrt, exp, sin. Вычисление квадратного корня или логарифма отрицательного числа не является ошибкой: в этом случае результатом является соответствующее комплексное число. MATLAB также предоставляет и более сложные функции, включая Гамма функцию и функции Бесселя. Большинство из этих функций имеют комплексные аргументы. Чтобы вывести список всех элементарных математических функций, наберите:

help elfun

Для вывода более сложных математических и матричных функций, наберите

help specfun

help elmat

Некоторые функции, такие как sqrt и sin, - встроенные. Они являются частью MATLAB, поэтому они очень эффективны, но их вычислительные детали трудно доступны. В то время как другие функции, такие как gamma и sink, реализованы в виде программного кода в М-файлах. Поэтому вы можете легко увидеть их код и, в случае необходимости, даже модифицировать его.

Задание векторов и матриц

Вы можете вводить матрицы в MATLAB несколькими способами:

а) вводить полный список элементов

>>V=[1 2 3] – задает вектор, имеющий три элемента;

>>M=[1 2 3; 4 5 6; 7 8 9]; - задает матрицу 3х3;

>>V=[2+2/(3+4) exp(5) sqrt(10)]; - задает значение выражения в качестве элементов матрицы.

>> A(1:5,1:5)=0 A = 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 >> A(1,:)=1 A = 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

>> A(end,3:end)=-1 A = 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 -1 -1

б) генерировать матрицы, используя встроенные функции

Имеется ряд специальных функций для задания векторов и матриц. Например, функция magic(n) задает магическую матрицу размера nxn, у которой сумма всех столбцов, всех строк и даже диагоналей равна одному и тому же числу:

>>M=magic(4), а также:

zeros все нули

ones все единицы

rand равномерное распределение случайных элементов

randn нормальное распределение случайных элементов

eye единичная матрица (в диагонали единицы)

>>Z = zeros(2,4)

>>F = 5*ones(3,3)

>>N = 10*rand(1,10)

в) загружать матрицы из внешних файлов

Команда load считывает двоичные файлы, содержащие матрицы, созданные в MATLAB ранее, или текстовые файлы, содержащие численные данные. Текстовые файлы должны быть сформированы в виде прямоугольной таблицы чисел, отделенных пробелами, с равным количеством элементов в каждой строке.

Например, создадим вне MATLAB текстовой файл, содержащий 4 строки:

16.0	3.0	2.0	13.0
5.0	10.0	11.0	8.0
9.0	6.0	7.0	12.0
4.0	15.0	14.0	1.0

Сохраним этот файл под именем magik . dat. Тогда команда load magik . dat прочитает этот файл и создаст переменную magik, содержащую нашу матрицу.

г) загружать матрицы из М-файлов

Вы можете создавать свои собственные матрицы, используя М-файлы, которые представляют собой текстовые файлы, содержащие код MATLAB. Просто создайте файл с выражением, которое вы хотите написать в командной строке MATLAB. Сохраните его в файле с расширением .m.[2]

Например, создадим файл, содержащий строку:

A=[16 3 2 13; 5 10 11 8; 9 6 7 12; 4 15 14 1];

Сохраним его под именем magik . m. Тогда выражение magik прочитает файл и создаст переменную А, содержащую исходную матрицу.

Замечание: Очень часто необходимо произвести формирование упорядоченных числовых последовательностей (числовых массивов - векторов). Первоначальное создание таких массивов производится с помощью оператора ":" (без кавычек)

{Начальное_значение}:{Шаг}:{Конечное_значение}

Пример:

>>1:5

>>i=0:2:10

>>x=1:-.2:0

>>x=0:5

Построение графиков функций

MATLAB позволяет строить графики функций в линейном, логарифмическом и полулогарифмическом масштабах. Общий порядок построения графиков функций:

• Задать аргумент в формате x={нач. значение}:{шаг}:{кон. значение}.

• Вычислить функцию, например, y=f(x).

• Построить график функции при помощи функции plot( x, y, s)

Построение графиков функций одной переменной в линейном масштабе осуществляется при помощи функции plot. В зависимости от входных аргументов функция plot позволяет строить один или несколько графиков, изменять цвет и стиль линий и добавлять маркеры на каждый график.

Функция plot имеет различные формы, связанные с входными параметрами, например plot( y) создает график зависимости элементов у от их индексов. Если вы задаете два вектора в качестве аргументов, plot( x, y) создаст график зависимости у от х. Например, для построения графика значений функции sin от нуля до 2, сделаем следующее

t = 0:pi/100:2*pi;

у = sin(t) ;

plot(t,у)

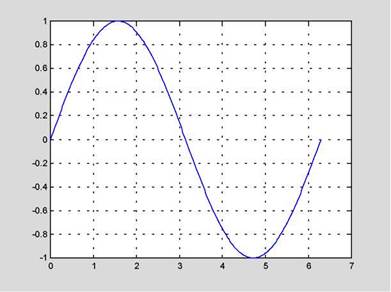
Рис. 1.1. График функции y= sin( x)

Возможно задание цвета, стиля линий и маркеров графиков при создании графика, с помощью параметра команды plot:

plot(x, у, ' s'),

где s – строковая константа, задающая параметры линии графика:

Таблица 1.1

Если на одном графике нужно отобразить несколько функций, например, y1=f(x) и y2=f(x), то они вначале вычисляются, а затем выводятся процедурой plot(x,y1,'s1',x,y2,'s2'...), в которой в качестве параметров для каждой функции следуют группы <аргумент, функция, тип линии>.

у2 = sin(t-.25);

уЗ = sin(t-.5);

plot(t, y, 'b', t, y2, 'g', t, уЗ, 'r')

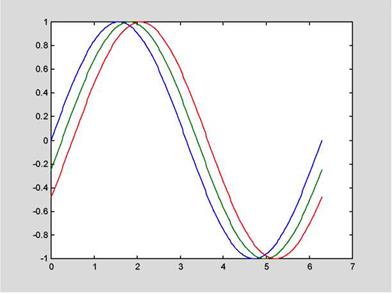
Рис. 1.2. Изображение нескольких функций на одном графике y= sin( x)

Удобство использования графиков во многом зависит от дополнительных элементов оформления: координатной сетки, подписей к осям, заголовка и легенды.

Управление осями

Производится с помощью функции axis. Она имеет несколько возможностей для настройки масштаба, ориентации и коэффициента сжатия.

axis({xmin xmax ymin ymax})

Обычно MATLAB находит максимальное и минимальное значение и выбирает соответствующий масштаб осей. Функция axis заменяет значения по умолчанию предельными значения, вводимыми пользователем. Также можно использовать ключевые слова для управления внешним видом осей. Например:

axis square – создает х и у оси равной длины,

axis equal – создает отдельные отметки приращений для х и у осей одинаковой длины.

Тогда, функция: plot(exp(i* t)), следующая либо за axis square, либо за axis equal превращает овал в правильный круг.

axis auto – возвращает значения по умолчанию и переходит в автоматический режим;

axis on – включает обозначения осей и метки промежуточных делений;

axis off – выключает обозначения осей и метки промежуточных делений;

Замечание: Иногда требуется сравнить поведение двух функций, значения которых сильно отличаются друг от друга. График функции с небольшими значениями практически сливаются с осью абсцисс, и установить его вид не удается. В этой ситуации помогает функция plotyy, которая выводит графики в окно с двумя вертикальными осями, имеющими подходящий масштаб.

Сетка наносится командой grid on, подписи к осям размещаются при помощи xlabel, ylabel, заголовок задается командой title. Наличие нескольких графиков на одних осях требует помещения легенды командой legend с информацией о линиях.

Пример: Следующие команды выводят графики изменения суточной температуры.

>> time = [0 4 7 9 10 11 12 13 13.5 14 14.5 15 16 17 18 20 22];

>> temp1 = [14 15 14 16 18 17 20 22 24 28 25 20 16 13 13 14 13];

>> temp2 = [12 13 13 14 16 18 20 20 23 25 25 20 16 12 12 11 10];

>> plot(time, temp1, ‘ro-‘, time, temp2, ‘go-’)

>> grid on

>> title(‘Суточные температуры’)

>> xlabel(‘Время (час.)’)

>> ylabel(‘Температура (С)’)

>> legend(’10 мая’, ’11 мая’)

Замечание: Дополнительным аргументом legend может быть положение легенды в графическом окне:

-1 – вне графика в правом верхнем углу графического окна;

0 – выбирается лучшее положение в пределах графика так, чтобы как можно меньше перекрывать сами графики;

1 – в верхнем правом углу графика (по умолчанию)

2 – в верхнем левом углу графика

3 – в нижнем левом углу графика

4 – в нижнем левом углу графика.

Использование ТЕХ-представления позволяет применять греческие буквы, математические символы и различные шрифты. Следующий пример демонстрирует эту возможность:

t = -pi:pi/100:pi;

у = sin(t) ;

plot(t,у)

axis([-pi pi -1 1])

xlabel( ' -\pi \leq \itt \leq \pi ' )

ylabel( ' sin(t) ' )

title( ' График функции sin ' )

text(-l, -1/3, ' \it{Oтмeтьте нечетную симметрию} ' )

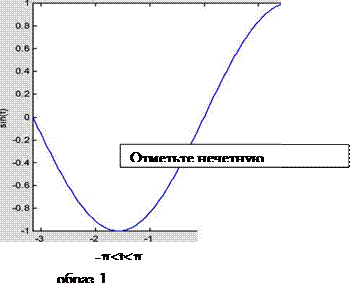Рис. 1.3. График функции y= sin( x)

1.4.4 Окна изображений

Функция plot автоматически открывает новое окно изображения (далее окно), если до этого его не было на экране. Если же оно существует, то plot использует его очищая его содержимое.

Для открытия нового окна и выбора его по умолчанию, наберите:

figure

Для того, чтобы сделать существующее окно текущим –

figure(n),

где n - это номер в заголовке окна. В этом случае результаты всех последующих команд будут выводиться в это окно.

Замечание: Чтобы добавить кривые на существующий график, следует воспользоваться командой hold on. Команда clf очищает все текущее окно. Команда cla – убирает только график, а оси, заголовок и названия осей оставляет

Подграфики

Функция subplot позволяет выводить множество графиков в одном окне или распечатывать их на одном листе бумаги.

subplot({m},{n},{p}) -

Разбивает окно изображений на матрицу m на n подграфиков и выбирает р-ый подграфик текущим. Графики нумеруются вдоль первого в верхней строке, потом во второй и т.д. Например, для того, чтобы представить графические данные в четырех разных подобластях окна необходимо выполнить следующее:

t = -pi:pi/100:pi;

x = cos(t) ;

у = sin(t) ;

z = 1/sin(t);

k = 1/cos(t) ;

subplot(2,2,1); plot(t,x)

subplot(2,2,2); plot(t,у)

subplot(2,2,3); plot(t,z)

subplot(2,2,4); plot(t,k)

Выполните задание к разделу 4: (задание 2 на стр. 25).

Основы трехмерной графики

MATLAB предоставляет различные способы визуализации функций двух переменных – построение трехмерных графиков и линий уровня, параметрически заданных линий и поверхностей.

Для формирования трехмерных графиков необходимо:

- Сгенерировать матрицы с координатами узлов сетки на прямоугольной области определения функции.

- Вычислить функцию в узлах сетки и записать полученные значения в матрицу.

- Использовать одну из графических функций MATLAB.

Генерация сетки

Сетка генерируется при помощи команды meshgrid, вызываемой с двумя аргументами, векторами, элементы которых соответствуют сетке прямоугольной области построения функции. Можно использовать один аргумент, если область построения функции – квадрат.

[X,Y] = meshgrid(x,y) – преобразует область, заданную векторами x,y в массивы X и Y, которые могут быть использованы для вычисления функции двух переменных и построения трехмерных графиков.

Пример:

>> [X,Y] = meshgrid(-1:0.5:1, 0:0.5:1)

>> [X,Y] = meshgrid(-1:0.05:1, 0:0.05:1);

[X,Y] = meshgrid(x) – аналогична [X,Y] = meshgrid(x,x)

Рис. 1.4. Трехмерный график с аксонометрией

Задание свойств линий и маркеров для plot3() производится также как и для plot()

plot3(X,Y,Z,S)

>> plot3(X,Y,Z,’-o’)

plot3(x1,y1,z1,s1, x2,y2,z2,s2,…)

>> plot3(X,Y,Z,’-k’,Y,X,Z,’-k’)

Наиболее представительными и наглядными являются сетчатые графики поверхностей с заданной или функциональной окраской. В названии их команд присутствует слово mesh. Имеется три группы таких команд:

Рис. 1.5. Сетчатый 3D-график с функциональной окраской

Цвет линий соответствует значениям функции. MATLAB рисует только видимую часть поверхности. При помощи команды hidden off можно сделать каркасную модель «прозрачной», добавив скрытую часть. MATLAB имеет несколько функций, возвращающих матричный образ поверхностей. Например, функция peaks(N) возвращает матричный образ поверхности с рядом пиков и впадин. Такие функции удобно использовать для проверки команд трехмерной графики.

Пример:

>> z = peaks(25);

>> mesh(z)

1.5.4 Сетчатый 3D-график с функциональной окраской и проекцией

Иногда график поверхности полезно объединить с контурным графиком ее проекции на плоскость, расположенным под поверхностью.

meshc(…)

>> [X,Y] = meshgrid([-3:0.15:3]);

>> Z=X.^2+Y.^2;

>> meshc(X,Y,Z)

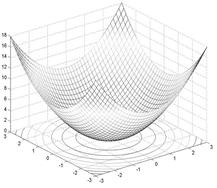
Рис. 1.6. Сетчатый 3D-график с функциональной окраской и проекцией

График такого типа дает лучшее представление об особенностях поверхности.

1.5.5 Поверхностный 3D-график с функциональной окраской

Наглядное представление о поверхностях дают графики, использующие функциональную закраску ячеек. Например, цвет окраски поверхности z(x,y) может быть поставлен в соответствие с высотой z поверхности с выбором для малых высот темных тонов, а для больших – светлых.

Для построения таких поверхностей используются команды класса surf(…).

surf(X,Y,Z,C) – строит цветную параметрическую поверхность по данным матриц X,Y и Z с цветом, задаваемым массивом C.

surf(X,Y,Z) – аналогична предшествующей команде, где C=Z.

Пример

>> [X,Y] = meshgrid([-3:0.15:3]);

>> Z=X.^2+Y.^2;

>> surf(X,Y,Z)

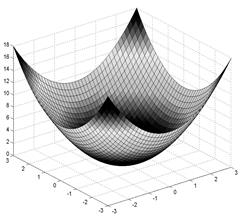
Рис. 1.7. Поверхностный 3D-график с функциональной окраской

>> colormap('') – задает окраску тонами определенного цвета

>> shading interp – обеспечивает устранение изображения сетки и задает интерполяцию для оттенков цвета объемной поверхности

Применение интерполяции для окраски придает поверхностям и фигурам более реалистичный вид, но фигуры каркасного вида дают более точные количественные данные о каждой точке.

1.5.6 Поверхностный 3D-график с функциональной окраской и освещением

Пожалуй, наиболее реалистичный вид имеют графики поверхностей, в которых имитируется освещение от точечного источника света, расположенного в заданном месте координатной системы. Графики имитируют оптические эффекты рассеивания, отражения и зеркального отражения света. Для получения таких эффектов используется команда surfl.

surfl(Z,S) или surfl(X,Y,Z,S) – строит графики поверхности с подсветкой от источника света, положение которого в системе декартовых координат задается вектором S=[Sx,Sy,Sz], а в системе сферических координат – вектором S=[AZ,EL];

При использовании surfl удобно задавать цветовые палитры: copper , bone, gray, pink, в которых интенсивность цвета изменяется линейно.

Пример.

>> [X,Y] = meshgrid(-1:0.05:1, 0:0.05:1);

>> Z = 4*sin(2*pi*X).*cos(1.5*pi*Y).*(1-X.^2).*Y.*(1-Y);

>> surfl(X,Y,Z)

>> colormap(‘copper’)

>> shading interp

По умолчанию источник света имеет азимут, больший на 45, чем наблюдатель, и тот же угол возвышения. Возможно изменение азимута источника. Например, изменим азимут до -90 по отношению к наблюдателю, а угол возвышения до нуля.

>> [Az , El] = view;

>> surfl(X,Y,Z,[Az-90,0])

>> shading interp

Азимут отсчитывается от оси, противоположной оси y, а угол возвышения - от плоскости xy.

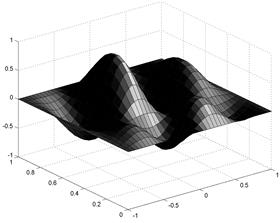
Рис. 1.8. Поверхностный 3D-график с функциональной окраской и освещением

Выполните задание к разделу 5: (задание 3 на стр. 26).

Управление потоками

MATLAB имеет пять видов структур управления потоками:

• оператор if

• оператор switch

• циклы for

• циклы while

• оператор break

В том случае, когда некоторая группа операций должна повторно выполняться несколько раз, используют операторы цикла.

а) оператор цикла с неизвестным числом повторений ( while)

while выражение

<оператор>

. . .

<оператор>

end

Операторы, указанные в теле цикла, выполняются, пока выражение истинно.

Пример:

fact=1;

k=1;

while fact<1e5

fact=fact*k;

k=k+1;

end

б) оператор цикла с известным числом повторений ( for)

for переменная цикла = начальное значение : <приращение> : конечное значение

<оператор>

. . .

<оператор>

end

Операторы, указанные в теле цикла, выполняются заданное число раз. При этом переменная цикла последовательно принимает все значения от начального до конечного с приращением после каждого прохода цикла.

for i=1:1:100

s= s+5

end

Замечание: Хорошим стилем являются отступы при использовании циклов для лучшей читаемости, особенно, когда они вложенные.

for i = 1:m

for j = 1:n

H(i,j) = 1/(i+j);

end ;

end

в) оператор условного ветвления

if <логическое выражение> <операторы> end

if <логическое выражение>

<операторы>

elseif <логическое выражение>

<операторы>

else

<операторы>

end

if <логическое выражение> <операторы> else <операторы> end

Оператор else не содержит логического условия. Инструкции, связанные с ним, выполняются, если предшествующий оператор if ложен.

Оператор elseif содержит логическое условие, которое вычисляется, если предшествующий оператор if ложен. Оператор elseif может многократно использоваться внутри оператора условия if.

Пример:

if n<0

a=2*n;

elseif rem(n,2)==0;

a=n/2;

else

a=(n+1)/2; Если n>0 b нечетное, увеличить на 1 и разделить.

end

Г ) оператор переключения

switch…case…otherwise…end

Оператор switch работает, сравнивая значение вычисленного выражения со значениями групп case. Если значение выражения в операторе switch совпадает со значением, указанным в case, то выполняются соответствующая группа операций до следующего оператора case или otherwise, или end. Оператор otherwise выполняется, если <выражение> не совпало ни с одним из значений.

Пример:

switch input_num % выч. выражение

case –1 % значение

disp ('минус один') % выводит строку text в рабочее окно MATLAB

case 0

disp ('нуль')

case 1

disp ('плюс один')

otherwise

disp ('другое значение')

end

д) оператор досрочного выхода из цикла

break

Оператор break позволяет досрочно выходить из циклов for или while. Во вложенных циклах break осуществляет выход только из самого внутреннего цикла.

for i=1:1:100

s=s+5

if s>300 then

break;

end;

end

1.6.2 Работа c М-файлами

Если требуется выполнять большую последовательность команд или повторять группу команд для различных значений входных переменных, работа в режиме командной строки становится неудобной. Для облегчения работы MATLAB предоставляет возможность организации вычислений в виде так называемых М-файлов. М-файлы являются обычными текстовыми файлами, которые содержат последовательности команд, операторов, функций и т.д., необходимых для вычислений. В состав системы MATLAB входит редактор/отладчик M-файлов. Наиболее удобно использовать инструментальную панель командного окна этого редактора/отладчика.

Для создания м-файла в меню File основного окна MatLab и в пункте New выберите подпункт M-file. Новый файл открывается в редакторе М-файлов. Наберите в редакторе команды, приводящие к построению двух графиков в одном графическом окне.

x = [0:0.1:7];

f = exp(-x);

subplot(1, 2, 1)

plot(x, f)

g = sin(x);

subplot(1, 2, 2)

plot(x, g)

Сохраните теперь файл с именем mydemo.m в подкаталоге work основного каталога MatLab, выбрав пункт Save as меню File редактора. Для запуска на выполнение всех команд, содержащихся в файле, следует выбрать пункт Run в меню Debug. На экране появится соответствующее графическое окно. Созданный М-файл можно как угодно редактировать и повторять все команды заново. При этом графическое окно будет отражать все изменения, которые вы сделали в файле. Для выполнения только части команд из файла, следует их сначала выделить, а затем выполнить из пункта Evaluate selection меню Text.

В редакторе М-файлов может быть открыто одновременно несколько файлов; переход от одного к другому осуществляется при помощи закладок с их именами внизу окна редактора. Открытие существующего М-файла производится из пункта Open меню File рабочей среды, либо редактора М-файлов.

1.6.3 Типы М-файлов. Файл-программы и файл-функции

М-файлы бывают двух типов: файл-программы (Script M-files), содержащие последовательность команд, и файл-функции (Function M-files), в которых описываются функции, определяемые пользователем для своих целей. Файл mydemo, который Вы уже создали, это файл-программа. Все переменные, объявленные в ней, становятся доступными в рабочей среде после ее выполнения. Фактически, созданный М-файл является новой командой, которую понимает МatLab. Теперь в командной строке достаточно набрать команду mydemo и появится графическое окно, соответствующее командам программы mydemo.m.

Как правило, М-файлы хранятся в каталоге пользователя. Чтобы МatLab мог найти их, следует установить пути, указывающее расположение М-файла.

Файл-программы являются последовательностью команд и не имеют входных и выходных аргументов. Для использования численных методов и при программировании собственных приложений необходимо уметь составлять файл-функции, которые выполняют действия с входными аргументами и возвращают результат в выходных аргументах.

Предположим, что в вычислениях часто необходимо использовать функцию

Имеет смысл один раз написать файл-функцию, чтобы потом вызывать ее всюду, где необходимо.

Откройте в редакторе М-файлов новый файл и наберите текст

function f = myfun(x)

f = exp(-x)*sqrt((x^2+1)/(x^4+0.1));

Слово function в первой строке означает, что данный файл содержит файл-функцию. Первая строка является заголовком файл-функции, где размещается имя функции myfun, один входной аргумент x и один выходной – f. После заголовка следует тело функции (здесь это одна строка), где и вычисляется ее значение. Теперь сохраните файл в рабочем каталоге (укажите полностью Ваш путь). При сохранении появляется диалоговое окно с уже готовым именем myfun. Не изменяйте его.

Теперь созданную функцию можно использовать так же, как и встроенные функции, из командной строки:

>> y=myfun(1.3)

y =

0.2600

Задания к лабораторной работе № 1

Задание 1

Таблица 1.2

1.Создать матрицу A
Вариант1	Вариант2	Вариант3	Вариант4	Вариант5	Вариант6	Вариант7	Вариант8
-1 2 3 5 7 8 9 1 4 5 6 4 11 1 5 9	8 4 6 9 2 7 4 10 3 8 2 6 -5 3 7 3	8 9 13 2 -6 6 4 5 8 4 6 4 13 1 8 9	8 6 7 5 7 3 7 15 4 8 9 2 8 9 8 5	1 -2 3 5 -7 8 9 1 11 3 2 4 1 1 4 -9	1 5 3 2 6 7 3 6 3 4 6 7 1 5 8 2	-1 2 3 5 3 8 9 1 5 3 6 4 7 7 5 1	1 5 6 4 2 8 9 1 4 8 6 4 4 5 5 -1
Вариант9	Вариант10	Вариант11	Вариант12	Вариант13	Вариант14	Вариант15	Вариант16
-1 4 8 5 7 7 9 2 4 8 6 1 1 1 4 0	-4 4 6 9 2 5 4 10 3 8 -6 6 8 3 7 2	5 4 3 2 -4 6 -4 5 8 5 6 2 3 1 8 91	8 6 7 51 0 7 -3 15 6 8 11 2 8 9 14 5	1 2 -3 15 5 8 -9 1 1 5 2 6 1 11 -5 -7	1 4 13 2 6 7 -4 6 3 -2 6 9 1 15 4 2	-5 2 -5 5 3 2 3 1 1 3 3 4 0 -2 0 1	1 0 6 4 2 5 9 -11 5 9 0 4 6 5 5 -1
Вариант17	Вариант18	Вариант19	Вариант20	Вариант21	Вариант22	Вариант23	Вариант24
0 9 13 2 -6 0 4 3 1 4 2 4 1 1 0 1	1 -3 3 5 -7 8 -6 1 11 0 0 4 0 1 4 -9	-3 21 5 -2 -3 1 3 1 -1 3 2 4 1 0 1 0	-4 5 1 9 2 5 0 10 1 8 -4 6 1 3 1 3	-1 3 6 9 2 5 3 10 5 12 2 6 1 1 1 1	7 5 2 4 2 7 9 17 -4 1 -5 7 1 4 2 1
2. Вычислить сумму элементов матрицы А по строкам, по столбцам, а также сумму всех элементов матрицы A.
3. Транспонировать матрицу A.
4.Умножить матрицу А на 2.
5. Найти квадратный корень из элементов матрицы А.
6 .Возвести в квадрат все элементы матрицы A.
7.Создать массив X, содержащий 2 строки:

Вариант 1

1 строка - числа от 1 до 100, в порядке возрастания

2 строка - числа от 1 до 100, в порядке убывания

1 строка - нечетные числа от 1 до 100, в порядке возрастания

2 строка – четные числа от 1 до 100, в порядке возрастания

1 строка - нечетные числа от 1 до 100, в порядке возрастания

2 строка - нечетные числа от 1 до 100, в порядке убывания

1 строка - числа от 1 до 100, кратные 3-м, в порядке возрастания

2 строка - числа от 1 до 100, кратные 3-м, в порядке убывания

1 строка - числа от 1 до 100, кратные 4-м, в порядке возрастания

2 строка - числа от 1 до 100, кратные 4-м, в порядке убывания

1 строка - числа от 1 до 100, кратные 5-и, в порядке возрастания

2 строка - числа от 1 до 100, кратные 5-и, в порядке убывания

1 строка - числа от 1 до 100, кратные 6-и, в порядке возрастания

2 строка - числа от 1 до 100, кратные 6-и, в порядке убывания

1 строка - числа от 1 до 100, кратные 7-и, в порядке возрастания

2 строка - числа от 1 до 100, кратные 7-и, в порядке убывания

1 строка - нечетные числа от 1 до 100, в порядке убывания

2 строка – четные числа от 1 до 100, в порядке возрастания

1 строка - четные числа от 1 до 100, в порядке убывания

2 строка – нечетные числа от 1 до 100, в порядке убывания

1 строка - числа от 1 до 100, кратные 3-м, в порядке убывания

2 строка - числа от 1 до 100, кратные 3-м, в порядке возрастания

1 строка - числа от 1 до 100, в порядке убывания

2 строка - числа от 1 до 100, в порядке возрастания

1 строка - числа от 1 до 100, кратные 6-и, в порядке убывания

2 строка - числа от 1 до 100, кратные 6-и, в порядке возрастания

1 строка - числа от 1 до 100, кратные 7-и, в порядке убывания

2 строка - числа от 1 до 100, кратные 7-и, в порядке убывания

1 строка - числа от 1 до 100, кратные 7-и, в порядке убывания

2 строка - числа от 1 до 100, кратные 7-и, в порядке возрастания

1 строка - числа от 1 до 100, кратные 7-и, в порядке возрастания

2 строка - числа от 1 до 100, кратные 7-и, в порядке возрастания

1 строка - числа от 1 до 100, кратные 4-м, в порядке возрастания

2 строка - числа от 1 до 100, кратные 4-м, в порядке возрастания

1 строка - числа от 1 до 100, кратные 4-м, в порядке убывания

2 строка - числа от 1 до 100, кратные 4-м, в порядке убывания

1 строка - числа от 1 до 100, кратные 4-м, в порядке убывания

2 строка - числа от 1 до 100, кратные 4-м, в порядке возрастания

1 строка - четные числа от 1 до 100, в порядке убывания

2 строка – четные числа от 1 до 100, в порядке убывания

1 строка - числа от 1 до 100, кратные 3-м, в порядке возрастания

2 строка - числа от 1 до 100, кратные 3-м, в порядке возрастания

1 строка - числа от 1 до 100, в порядке убывания

2 строка - числа от 1 до 100, в порядке убывания

ЛАБОРАТОРНАЯ РАБОТА № 2

Подготовительная часть.

Для выполнения лабораторной работы необходимо повторить следующие вопросы:

1. Вычисление площади фигуры, ограниченной кривыми.

2. Понятие и расчет доверительного интервала.

Теоретическая часть.

Пример 1. Пусть требуется определить площадь круга известного диаметра с помощью выборок из значений случайной величины. Впишем круг в квадрат; таким образом, стороны квадрата будут равны диаметру круга.

Пусть круг имеет радиус г=5 см и его центр в точке (0,0).

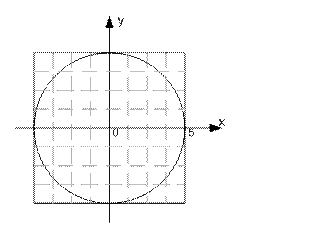
Уравнение окружности будет иметь вид

x²+ y²=25

Описанный квадрат определяется его вершинами (—5, 5), (5, 5), (5, -5) и (-5, -5), которые получаются непосредственно из геометрических свойств фигуры. Любая точка (х, у) внутри квадрата или на его границе должна удовлетворять неравенствам —5≤х≤5 и —5≤у≤5

Применение выборок при использовании метода Монте-Карло основано на предположении, что все точки в квадрате —5≤х≤5 и —5≤у≤5 могут появляться с одинаковой вероятностью, т. е. х и у распределены равномерно с плотностями вероятности

1/10, —5≤х≤5

f(x)=

0 в противном случае

1/10, —5≤y≤5

f(y)=

0 в противном случае

Определим теперь точку (х, у) в соответствии с распределениями f( x) и f(у). Продолжая этот процесс, подсчитаем число точек, попавших внутрь круга или на окружность. Предположим, что выборка состоит из п наблюдений и т из п точек попали внутрь круга или на окружность. Тогда

оценка площади круга = m/ n(площадь квадрата)=( m/ n)*(10*10)

Подобный способ оценивания площади круга можно обосновать тем, что в процессе получения выборки любая точка (х, у) может с одинаковой вероятностью попасть в любое место квадрата. Поэтому отношение m/ n представляет оценку площади круга относительно площади квадрата.

Использование Matlab для постановки эксперимента.

Для решения данной задачи в системе Matlab можно воспользоваться следующей М-функцией:

function[s]=sum(n)

m=0;

for i=1:n

x=Random('unif',-5,5);

y=Random('unif',-5,5);

if x*x+y*y<=25

m=m+1;

end;

s=(m/n)*100;

Здесь параметр ‘unif’ функции Random позволяет получить равномерно распределенное случайное число.

1. Обработка результатов

Для изучения влияния статистической ошибки при моделировании задача решалась для различных значений п, равных 150, 200, 500, 1000, 2000, 5000 и 10 000. Кроме того, при каждом п было проведено 10 прогонов, в каждом из которых использовались различные последовательности случайных чисел из интервала [-5, 5].

Номер
прогона

150

200

500

1000

2000

5000

80,5

78,6

79,55

78,32

79,5

79,6

78,8

78,85

79,26

81,5

76,6

77,6

79,1

77,22

78,8

79,55

79,34

76,2

79,8

79,4

79,22

77,5

76,6

77,6

77,4

77,44

81,5

80,4

78,5

78,1

79,28

76,5

81,8

79,7

77,2

78,82

80,5

76,6

76,4

77,76

78,74

81,2

78,4

77,74

Среднее

78,1

78,35

78,38

78,5

78,531

78,538

Дисперсия

23,65556

14,28056

5,035111

1,306667

0,789499

0,658618

Расчетное значение

78,54

В таблице приведены результаты эксперимента, исходя из которых можно сделать следующие заключения.

1. С ростом числа генерируемых точек (т. е. продолжительности прогона модели) оценки площади круга приближаются к точному значению (78,54 см²). На рис. 2 показаны оценки площади прогонов 1 и 2 в зависимости от продолжительности прогона п. Мы видим, что сначала оценки колеблются около точного значения, а затем стабилизируются. Это условие обычно достигается после повторения эксперимента достаточное количество раз. Наблюдаемое явление типично для результатов любой имитационной модели. Обычно в большинстве имитационных моделей нас интересуют результаты, полученные в стационарных условиях.

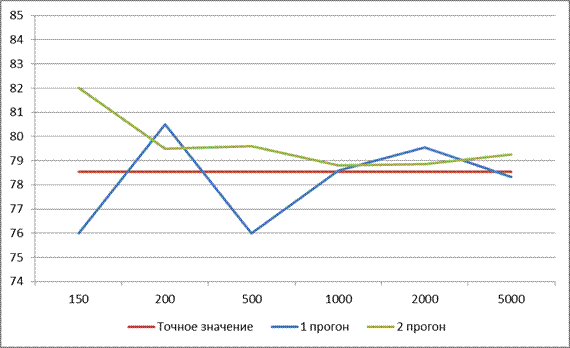
Рис. 2

2. Влияние переходных условий уменьшается, если усреднить результаты 10 серий. Это иллюстрирует рис. 3, на котором показана зависимость среднего от п. Кроме того, на рисунках видно, что для каждого п при достижении стационарных условий дисперсия убывает. При возрастании п от 150 до 200 дисперсия резко уменьшается с 23,66 до 14,25. За исключением этого интервала, столь резкого уменьшения дисперсии нигде больше не наблюдается. Последнее замечание указывает на то, что существует предел, за которым увеличение продолжительности прогона модели уже не дает существенного повышения точности результата, измеряемой дисперсией. Это замечание представляется чрезвычайно важным, поскольку затраты на эксплуатацию имитационной модели прямо пропорциональны продолжительности прогонов. Поэтому желательно найти компромисс между большой точностью (т. е. малой дисперсией) и небольшими затратами на процедуру получения результатов.

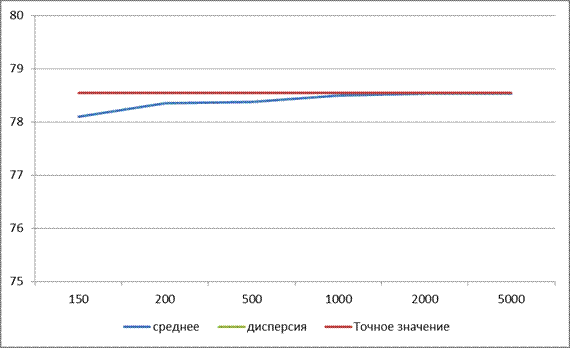
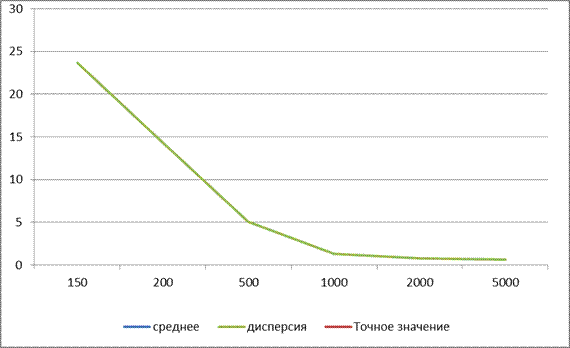
Рис.3.

3. Ввиду того что оценки площади имеют разброс, важно, чтобы результаты эксперимента, связанного с моделированием, были выражены в виде доверительных интервалов, показывающих величину отклонения от точного значений. В рассматриваемом примере, если А представляет собой точное значение площади, а 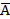и s² — среднее и дисперсию N наблюдений, то 100 (1—α)%-ный доверительный интервал для А задается как

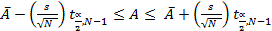
Задание (по вариантам)

1. Найти площадь фигуры, ограниченной линиями:

y=sin(x)+2

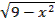
y=0

2. Найти площадь фигуры, ограниченной линиями:

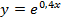
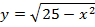
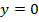
3. Найти площадь фигуры, ограниченной линиями:

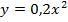
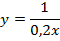
x=0

y=4

4. Найти площадь фигуры, ограниченной линиями:

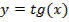
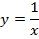
y=0

x=3

ЛАБОРАТОРНАЯ РАБОТА № 3

Тема. Моделирование временных характеристик

динамической системы с прямыми связями (2 часа)

Вопросы текущего контроля знаний

1. Дайте определение передаточной функции.

2. Поясните назначение элементов структурных схем: функционального блока; узла; сумматора.

Исходные данные

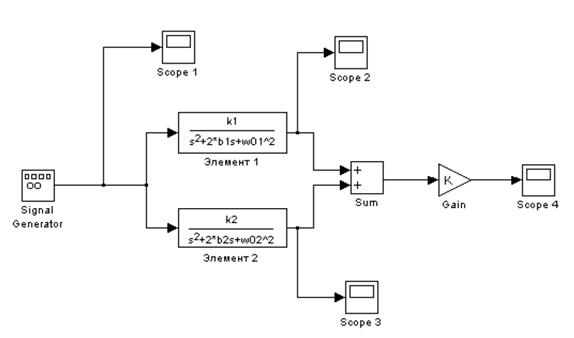
Замкнутая линейная динамическая система, состоящая из двух параллельных колебательных звеньев, описывается следующей системой уравнений:

ЛАБОРАТОРНАЯ РАБОТА № 4

Тема. Моделирование временных характеристик

динамической системы с обратной связью (2 часа)

Вопросы текущего контроля знаний

3. Раскройте понятие обратной связи.

4. Дайте определение передаточной функции системы по рассогласованию.

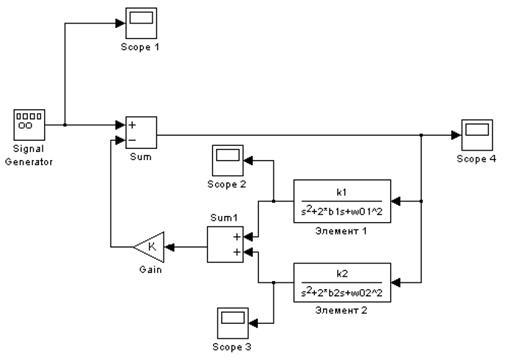
Исходные данные

Замкнутая линейная динамическая система с отрицательной обратной связью, состоящая из двух параллельных колебательных звеньев, описывается следующей системой уравнений:

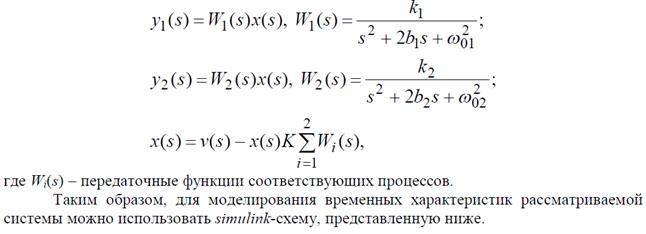
ЛАБОРАТОРНАЯ РАБОТА № 5

Тема. Моделирование временных характеристик динамической системы с перекрестными обратными связями (2 часа)

Вопросы текущего контроля знаний

1. Поясните принципиальные отличия классического и системного подходов.

2. Раскройте понятие перекрестной связи.

Исходные данные

Замкнутая линейная динамическая система с перекрестными обратными связями, состоящая из двух параллельных колебательных звеньев, описывается следующей системой уравнений:

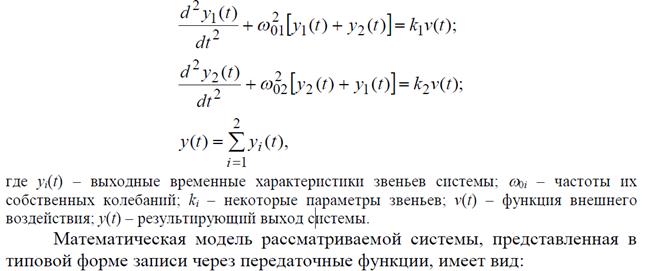
ЛАБОРАТОРНАЯ РАБОТА № 6

Тема. Комплексное моделирование характеристик

динамической системы с прямыми связями (2 часа)

Вопросы текущего контроля знаний

1. Раскройте понятие «математическое моделирование».

2. Поясните сущности вещественной и мнимой частотных характеристик системы.

Исходные данные

Математическая модель замкнутой линейной динамической системы, состоящей из двух параллельных колебательных звеньев, представленная в типовой форме записи через передаточные функции, имеет вид:

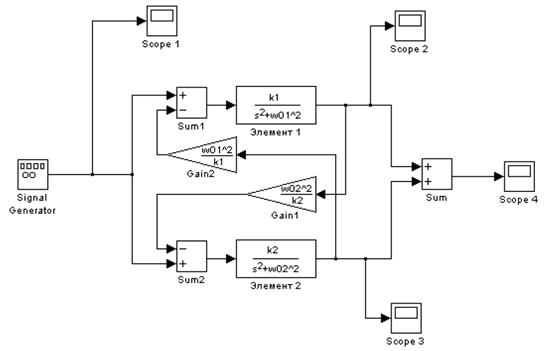
Цель работы

Целью лабораторной работы является изучение устройства, принципа работы и математических моделей электрических, гидравлических и пневматических рулевых приводов, а также анализ статической и динамических характеристик типового рулевого привода с помощью математической модели привода, составленной в системе программирования Матлаб.

Задание

При выполнение работы необходимо:

1. Изучить устройство, принцип работы и математические модели электрических, гидравлических и пневматических рулевых приводов (РП).

2. Для заданного варианта типового РП рассчитать и построить статическую характеристику привода при линейной и нелинейной моделях РП. Сравнить решения для линейной и нелинейной моделей.

3. Используя линейную модель РП, рассчитать экспериментально три значения логарифмических амплитудной и фазовой частотных характеристик (ЛАЧХ и ЛФЧХ) замкнутого РП при трех заданных значениях частоты гармонического входного сигнала.

4. С помощью блока LTI view Matlab рассчитать и построить графики ЛАЧХ и ЛФЧХ замкнутого РП.

5. Нанести значения ЛАЧХ и ЛФЧХ, рассчитанные в п.4. Сравнить экспериментальное и теоретическое решения.

6. Используя модели, рассчитать и построить переходные процессы на выходе линейной и нелинейной моделей РП при подаче на вход моделей ступенчатого воздействия. Сравнить решения для линейной и нелинейной моделей РП.

Порядок выполнения работы

Лабораторная работа выполняется бригадами на компьютерах.

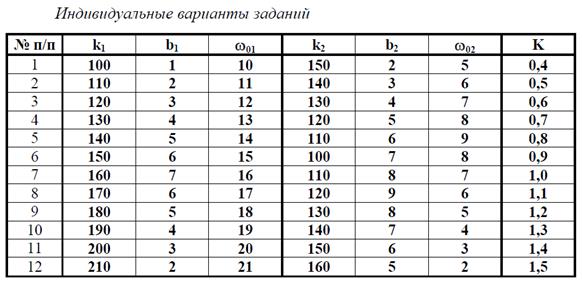
Бригада выполняет вариант задания, выдаваемый преподавателем. Варианты различаются исходными данными для проведения расчетов.

Все расчеты проводятся в системе программирования Matlab с использованием пакета визуального программирования Simulink.

Предполагается, что начальные навыки работы в Matlab и Simulink были получены студентами при выполнении первой лабораторной работы по данной дисциплине.

Требуется:

1. Рассчитать и построить статические характеристики рулевого привода при линейной и нелинейной моделях привода. Сравнить и объяснить полученные решения.

2. Определить экспериментально путем проведения компьютерного эксперимента с моделью привода значения логарифмических амплитудной и фазовой частотных характеристик замкнутого рулевого привода при трех значениях частоты гармонического входного сигнала 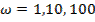рад/сек.

3. Рассчитать и построить логарифмические характеристики привода 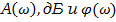, град. С помощью блока LTI view. Сравнить значения характеристик, полученные в п.2 экспериментально полученные значения.

4. Рассчитать и построить переходные процессы в приводе при нелинейной и линейной моделях привода.

Методика выполнения работы

Создание модели привода

Предварительно должны быть выполнены следующие действия:

1. Запустить MATLAB

2. Открыть приложение Simulink.

3. Создать программу моделирования линейного и нелинейного РП, показанную на рисунке.

Лабораторная работа №1

«Ознакомление с вычислительной системой MATLAB и ее использование для моделирования систем»

Цель лабораторной работы

Описание системы MATLAB

1.2.1 Краткая характеристика MATLAB

§ математические вычисления

§ создание алгоритмов

§ моделирование

§ анализ данных, исследования и визуализация

§ научная и инженерная графика

§ разработка приложений, включая создание графического интерфейса

Рабочая среда MATLAB содержит следующие элементы:

§ меню;

§ панель инструментов с кнопками и раскрывающимся списком;

§ командное окно Command Window;

§ строку состояния.

Настройка окон рабочей среды производится с помощью меню View и View -> Desktop Layout

Дополнительные возможности MATLAB

MATLAB в режиме прямых вычислений

Примеры:[1]

>>1+2

ans=3

>>ans/10

ans=0.08415

>>4*5; %(для блокировки вывода результата вычислений добавьте символ ";" (без кавычек) %в конец выражения)

>>sin(1)

ans=0.8415

Замечание:

ü Текстовый комментарий к выполняемым действиям в MATLAB можно ввести после знака %.

Дата: 2018-12-21, просмотров: 2734.

12 3 4 5 6 7 Следующая ⇒