Задание 2. Вычислить значения функций 1 и 2 (табл. 1.3) для аргумента в заданном интервале [ a b] c шагом h. Вывести графики функций одновременно на одном графике в декартовых координатах. Для разных графиков использовать разный тип линий.
Таблица 1.3
|
| |||||
| № | Функция 1 | Функция 2 | a | B | H |
| 1 | y = sin(x) | z= exp(x+3)/5000 - 1 | -2 | 2 | /20 |
| 2 | y = cos(x) | z = 0.00025e3-x - 0.6 | -2 | 2 | /20 |
| 3 | y = |tg(x)| + 0.1 | z = (1+x)6 | -2 | 2 | /20 |
| 4 | y = (x2-1)/15 | z = 1+sin(x) | -2 | 2 | /20 |
| 5 | y = (x3-2)/15 | z = 5cos(x) | -2 | 2 | /20 |
| 6 | y = x2 - 10 | z = 0.025exp(-1.2x) | -5 | 5 | 1 |
| 7 | y = 3sin(x) | z=0.015x3 | -5 | 5 | 1 |
| 8 | y = |sin(x)|exp(x/2) | z = 5x - x1.5+sin(x) | 0 | 5 | 0.5 |
| 9 | y = 0.5x3 | z = -2cos(x) | |||
| 10 | y = 2-sin(x) | z = cos(x) | -2 | 2 | /20 |
| 11 | y = exp(2x+1) | z = sin(x) | -2 | 2 | /20 |
| 12 | y = (x3-2)/15 | z = x2 - 1 | -2 | 2 | /20 |
| 13 | y = 6cos(x) | z = 0.5x2 | -2 | 2 | /20 |
| 14 | y = 5x2 | z = (x3-3)/11 | -2 | 2 | /20 |
| 15 | y = exp(-1.7x) | z = exp(-1.6x) | -5 | 5 | 1 |
| 16 | y = 5cos(x) | z = 7sin(x) | -5 | 5 | 1 |
| 17 | y = 1+cos(x) | z = (x3-6)/13 | -5 | 5 | 1 |
| 18 | y = (x3-3)/10 | z = 7x3 | -2 | 2 | /20 |
| 19 | y = 1+sin(x) | z = exp(-1.4x) | -2 | 2 | /20 |
| 20 | y = 8cos(x) | z = (x2-8)/33 | -2 | 2 | /20 |
| 21 | y = 6x2+5x2 | z = (x3-2)/4 | -5 | 5 | 1 |
| 22 | y = 6cos(x)+sin(x) | y = x2 | -2 | 2 | /20 |
Задание 3. Вычислить значения функции двух аргументов (табл. 1.4) в заданном диапазоне. Вывести функцию в виде 5 трехмерных графиков разного типа. Вывести функцию в виде 2 контурных графиков разного типа.
Таблица 1.4
| № | Функция | Пределы изменения | |
| x | y | ||
| 1 | z=sin(x)cos(y) | от -2 до 2 | от -2 до 2 |
| 2 | z=sin(x/2)cos(y) | от -2 до 2 | от -2 до 2 |
| 3 | z=sin(2x)cos(y) | от -2 до 2 | от -2 до 2 |
| 4 | z = sin(x)cos(y/2) | от -2 до 2 | от -2 до 2 |
| 5 | z = sin(x/2)cos(2y) | от -2 до 2 | от -2 до 2 |
| 6 | z = sin(2x)cos(2y) | от -2 до 2 | от -2 до 2 |
| 7 | z = (1+sin(x)/x)(sin(y)/y) | от -2 до 2 | от -2 до 2 |
| 8 | z = (sin(x)/x)cos(y) | от -2 до 2 | от -2 до 2 |
| 9 | z = sin(3x)cos(y/2) | от -2 до 2 | от -2 до 2 |
| 10 | z = (sin(3x)+3)cos(2y) | от -2 до 2 | от -2 до 2 |
| 11 | z = sin(x/3)cos(4y) | от -2 до 2 | от -2 до 2 |
| 12 | z = (4+sin(2x)/x)(sin(4y)/y) | от -2 до 2 | от -2 до 2 |
| 13 | z=sin(2x)cos(3y) | от -2 до 2 | от -2 до 2 |
| 14 | z = (-1+sin(x)/x)(sin(y)/3) | от -2 до 2 | от -2 до 2 |
| 15 | z = sin(x)cos(4y) | от -2 до 2 | от -2 до 2 |
| 16 | z = (3+sin(x)/3)(sin(2y)/y) | от -2 до 2 | от -2 до 2 |
| 17 | z = (1+sin(3x)/2)(1+sin(2y)/y) | от -2 до 2 | от -2 до 2 |
| 18 | z=sin(5x)cos(1.5y) | от -2 до 2 | от -2 до 2 |
| 19 | z = sin(5x)cos(2y) | от -2 до 2 | от -2 до 2 |
| 20 | z = sin(3x)cos(3y) | от -2 до 2 | от -2 до 2 |
| 21 | z = sin(x)cos(7y) | от -2 до 2 | от -2 до 2 |
| 22 | z = sin(9x)cos(4y) | от -2 до 2 | от -2 до 2 |
ЛАБОРАТОРНАЯ РАБОТА № 2
Имитационное моделирование для
Решения инженерно-вычислительных задач (методом Монте-Карло)
Подготовительная часть.
Для выполнения лабораторной работы необходимо повторить следующие вопросы:
1. Вычисление площади фигуры, ограниченной кривыми.
2. Понятие и расчет доверительного интервала.
Теоретическая часть.
Пример 1. Пусть требуется определить площадь круга известного диаметра с помощью выборок из значений случайной величины. Впишем круг в квадрат; таким образом, стороны квадрата будут равны диаметру круга.
Пусть круг имеет радиус г=5 см и его центр в точке (0,0).
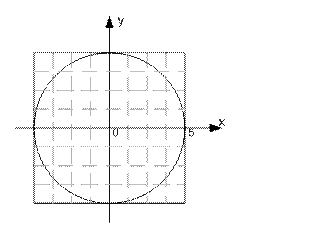
Уравнение окружности будет иметь вид
x2+ y2=25
Описанный квадрат определяется его вершинами (—5, 5), (5, 5), (5, -5) и (-5, -5), которые получаются непосредственно из геометрических свойств фигуры. Любая точка (х, у) внутри квадрата или на его границе должна удовлетворять неравенствам —5≤х≤5 и —5≤у≤5
Применение выборок при использовании метода Монте-Карло основано на предположении, что все точки в квадрате —5≤х≤5 и —5≤у≤5 могут появляться с одинаковой вероятностью, т. е. х и у распределены равномерно с плотностями вероятности
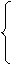 |
1/10, —5≤х≤5
f(x)=
0 в противном случае
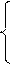 |
1/10, —5≤y≤5
f(y)=
0 в противном случае
Определим теперь точку (х, у) в соответствии с распределениями f( x) и f(у). Продолжая этот процесс, подсчитаем число точек, попавших внутрь круга или на окружность. Предположим, что выборка состоит из п наблюдений и т из п точек попали внутрь круга или на окружность. Тогда
оценка площади круга = m/ n(площадь квадрата)=( m/ n)*(10*10)
Подобный способ оценивания площади круга можно обосновать тем, что в процессе получения выборки любая точка (х, у) может с одинаковой вероятностью попасть в любое место квадрата. Поэтому отношение m/ n представляет оценку площади круга относительно площади квадрата.
Использование Matlab для постановки эксперимента.
Для решения данной задачи в системе Matlab можно воспользоваться следующей М-функцией:
function[s]=sum(n)
m=0;
for i=1:n
x=Random('unif',-5,5);
y=Random('unif',-5,5);
if x*x+y*y<=25
m=m+1;
end;
end;
s=(m/n)*100;
Здесь параметр ‘unif’ функции Random позволяет получить равномерно распределенное случайное число.
1. Обработка результатов
Для изучения влияния статистической ошибки при моделировании задача решалась для различных значений п, равных 150, 200, 500, 1000, 2000, 5000 и 10 000. Кроме того, при каждом п было проведено 10 прогонов, в каждом из которых использовались различные последовательности случайных чисел из интервала [-5, 5].
| Номер | ||||||
Дата: 2018-12-21, просмотров: 1043.