Наглядным способом представления векторных и матричных данных являются диаграммы и гистограммы. Значение элемента вектора пропорционально высоте столбика диаграммы (в случае столбчатой диаграммы) или площади сектора диаграммы (для круговой). Гистограммы используются для получения информации о распределении данных по заданным интервалам.
Функция bar отображает вектор в виде столбчатой диаграммы.
bar {X,Y,W}
>> data = [1.2 1.7 2.2 2.4 2.5 1.3 1.1 0.5 0.4 0.1];
>> bar(data)
по горизонтальной оси откладывается номер элемента вектора, а по вертикальной – его значение. Аргументом функции bar может быть как вектор-строка, так и вектор-столбец.
Для отображения значений элементов векторов в зависимости не от номера, а, например, от времени, если в вектор записаны результаты измерений в некоторые моменты времени, функция bar вызывается с двумя аргументами:
>> time = [0.0 0.1 0.2 0.4 0.5 0.8 1.1 1.3];
>> data = [2.85 2.93 2.99 3.26 3.01 2.25 2.09 1.79];
>> bar(time, data) – важно, чтобы размеры data и time совпадали
Выбор ширины столбцов осуществляется заданием третьего аргумента (по умолчанию она равна 0.8). Если ширина равна 1, то диаграмма получается без промежутков между столбцами.
Если требуется оценить вклад каждого из элементов вектора в общую сумму его элементов, то удобно построить круговую диаграмму – pie.
>> data = [19.5 13.4 42.6 7.9];
>> pie(data)
Часто необходимо отодвинуть от круга диаграммы сектор, соответствующий некоторому элементу.
>> data = [19.5 13.4 42.6 7.9];
>> parts = [0 1 0 0];
>> pie(data, parts) - важно, чтобы размеры data и parts совпадали
Обработка данных включает вопрос о том, сколько данных попало в тот или иной интервал. Для получения наглядного представления о распределении данных служит функция hist.
>> data = randn(100000,1);
>> hist(data)
Построение графиков функций
MATLAB позволяет строить графики функций в линейном, логарифмическом и полулогарифмическом масштабах. Общий порядок построения графиков функций:
• Задать аргумент в формате x={нач. значение}:{шаг}:{кон. значение}.
• Вычислить функцию, например, y=f(x).
• Построить график функции при помощи функции plot( x, y, s)
Построение графиков функций одной переменной в линейном масштабе осуществляется при помощи функции plot. В зависимости от входных аргументов функция plot позволяет строить один или несколько графиков, изменять цвет и стиль линий и добавлять маркеры на каждый график.
Функция plot имеет различные формы, связанные с входными параметрами, например plot( y) создает график зависимости элементов у от их индексов. Если вы задаете два вектора в качестве аргументов, plot( x, y) создаст график зависимости у от х. Например, для построения графика значений функции sin от нуля до 2, сделаем следующее
t = 0:pi/100:2*pi;
у = sin(t) ;
plot(t,у)
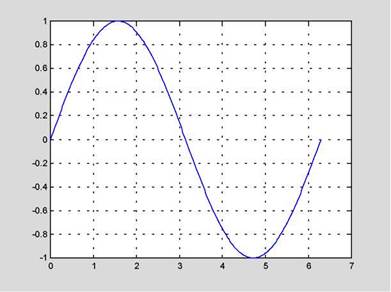
Рис. 1.1. График функции y= sin( x)
Возможно задание цвета, стиля линий и маркеров графиков при создании графика, с помощью параметра команды plot:
plot(x, у, ' s'),
где s – строковая константа, задающая параметры линии графика:
Таблица 1.1

Если на одном графике нужно отобразить несколько функций, например, y1=f(x) и y2=f(x), то они вначале вычисляются, а затем выводятся процедурой plot(x,y1,'s1',x,y2,'s2'...), в которой в качестве параметров для каждой функции следуют группы <аргумент, функция, тип линии>.
у2 = sin(t-.25);
уЗ = sin(t-.5);
plot(t, y, 'b', t, y2, 'g', t, уЗ, 'r')
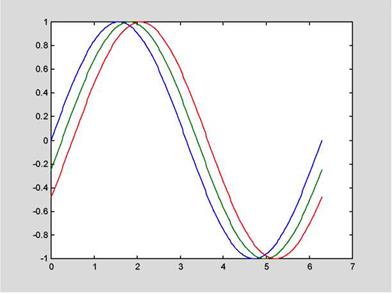
Рис. 1.2. Изображение нескольких функций на одном графике y= sin( x)
Удобство использования графиков во многом зависит от дополнительных элементов оформления: координатной сетки, подписей к осям, заголовка и легенды.
Управление осями
Производится с помощью функции axis. Она имеет несколько возможностей для настройки масштаба, ориентации и коэффициента сжатия.
axis({xmin xmax ymin ymax})
Обычно MATLAB находит максимальное и минимальное значение и выбирает соответствующий масштаб осей. Функция axis заменяет значения по умолчанию предельными значения, вводимыми пользователем. Также можно использовать ключевые слова для управления внешним видом осей. Например:
axis square – создает х и у оси равной длины,
axis equal – создает отдельные отметки приращений для х и у осей одинаковой длины.
Тогда, функция: plot(exp(i* t)), следующая либо за axis square, либо за axis equal превращает овал в правильный круг.
axis auto – возвращает значения по умолчанию и переходит в автоматический режим;
axis on – включает обозначения осей и метки промежуточных делений;
axis off – выключает обозначения осей и метки промежуточных делений;
Замечание: Иногда требуется сравнить поведение двух функций, значения которых сильно отличаются друг от друга. График функции с небольшими значениями практически сливаются с осью абсцисс, и установить его вид не удается. В этой ситуации помогает функция plotyy, которая выводит графики в окно с двумя вертикальными осями, имеющими подходящий масштаб.
Сетка наносится командой grid on, подписи к осям размещаются при помощи xlabel, ylabel, заголовок задается командой title. Наличие нескольких графиков на одних осях требует помещения легенды командой legend с информацией о линиях.
Пример: Следующие команды выводят графики изменения суточной температуры.
>> time = [0 4 7 9 10 11 12 13 13.5 14 14.5 15 16 17 18 20 22];
>> temp1 = [14 15 14 16 18 17 20 22 24 28 25 20 16 13 13 14 13];
>> temp2 = [12 13 13 14 16 18 20 20 23 25 25 20 16 12 12 11 10];
>> plot(time, temp1, ‘ro-‘, time, temp2, ‘go-’)
>> grid on
>> title(‘Суточные температуры’)
>> xlabel(‘Время (час.)’)
>> ylabel(‘Температура (С)’)
>> legend(’10 мая’, ’11 мая’)
Замечание: Дополнительным аргументом legend может быть положение легенды в графическом окне:
-1 – вне графика в правом верхнем углу графического окна;
0 – выбирается лучшее положение в пределах графика так, чтобы как можно меньше перекрывать сами графики;
1 – в верхнем правом углу графика (по умолчанию)
2 – в верхнем левом углу графика
3 – в нижнем левом углу графика
4 – в нижнем левом углу графика.
Использование ТЕХ-представления позволяет применять греческие буквы, математические символы и различные шрифты. Следующий пример демонстрирует эту возможность:
t = -pi:pi/100:pi;
у = sin(t) ;
plot(t,у)
axis([-pi pi -1 1])
xlabel( ' -\pi \leq \itt \leq \pi ' )
ylabel( ' sin(t) ' )
title( ' График функции sin ' )
text(-l, -1/3, ' \it{Oтмeтьте нечетную симметрию} ' )
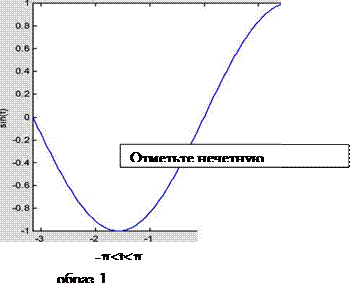 |
Рис. 1.3. График функции y= sin( x)
1.4.4 Окна изображений
Функция plot автоматически открывает новое окно изображения (далее окно), если до этого его не было на экране. Если же оно существует, то plot использует его очищая его содержимое.
Для открытия нового окна и выбора его по умолчанию, наберите:
figure
Для того, чтобы сделать существующее окно текущим –
figure(n),
где n - это номер в заголовке окна. В этом случае результаты всех последующих команд будут выводиться в это окно.
Замечание: Чтобы добавить кривые на существующий график, следует воспользоваться командой hold on. Команда clf очищает все текущее окно. Команда cla – убирает только график, а оси, заголовок и названия осей оставляет
Подграфики
Функция subplot позволяет выводить множество графиков в одном окне или распечатывать их на одном листе бумаги.
subplot({m},{n},{p}) -
Разбивает окно изображений на матрицу m на n подграфиков и выбирает р-ый подграфик текущим. Графики нумеруются вдоль первого в верхней строке, потом во второй и т.д. Например, для того, чтобы представить графические данные в четырех разных подобластях окна необходимо выполнить следующее:
t = -pi:pi/100:pi;
x = cos(t) ;
у = sin(t) ;
z = 1/sin(t);
k = 1/cos(t) ;
subplot(2,2,1); plot(t,x)
subplot(2,2,2); plot(t,у)
subplot(2,2,3); plot(t,z)
subplot(2,2,4); plot(t,k)
Выполните задание к разделу 4: (задание 2 на стр. 25).
Основы трехмерной графики
MATLAB предоставляет различные способы визуализации функций двух переменных – построение трехмерных графиков и линий уровня, параметрически заданных линий и поверхностей.
Для формирования трехмерных графиков необходимо:
- Сгенерировать матрицы с координатами узлов сетки на прямоугольной области определения функции.
- Вычислить функцию в узлах сетки и записать полученные значения в матрицу.
- Использовать одну из графических функций MATLAB.
Генерация сетки
Сетка генерируется при помощи команды meshgrid, вызываемой с двумя аргументами, векторами, элементы которых соответствуют сетке прямоугольной области построения функции. Можно использовать один аргумент, если область построения функции – квадрат.
[X,Y] = meshgrid(x,y) – преобразует область, заданную векторами x,y в массивы X и Y, которые могут быть использованы для вычисления функции двух переменных и построения трехмерных графиков.
Пример:
>> [X,Y] = meshgrid(-1:0.5:1, 0:0.5:1)
>> [X,Y] = meshgrid(-1:0.05:1, 0:0.05:1);
[X,Y] = meshgrid(x) – аналогична [X,Y] = meshgrid(x,x)
Дата: 2018-12-21, просмотров: 1197.