Команда plot3(…) является аналогом команды plot(…), но относится к функциям двух переменных z(x,y). Она строит аксонометрическое изображение трехмерных поверхностей.
plot3(x,y,z) – строит массив точек, представленных векторами x, y и z, соединяя их отрезками прямых.
Пример:
>> [X,Y] = meshgrid(-3:0.15:3);
>> Z=X.^2+Y.^2;
>> plot3(X,Y,Z)
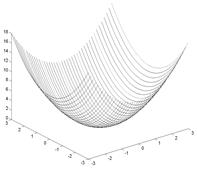
Рис. 1.4. Трехмерный график с аксонометрией
Задание свойств линий и маркеров для plot3() производится также как и для plot()
plot3(X,Y,Z,S)
>> plot3(X,Y,Z,’-o’)
plot3(x1,y1,z1,s1, x2,y2,z2,s2,…)
>> plot3(X,Y,Z,’-k’,Y,X,Z,’-k’)
Наиболее представительными и наглядными являются сетчатые графики поверхностей с заданной или функциональной окраской. В названии их команд присутствует слово mesh. Имеется три группы таких команд:
Сетчатый 3D-график с функциональной окраской
mesh(X,Y,Z,C) – выводит в окно сетчатую поверхность Z(X,Y) с цветами узлов поверхности, заданными массивом C.
mesh(X,Y,Z) – аналог предшествующей команды при C=Z.
Пример: Построить график функции двух переменных
z(x, y) = 4sin2xcos1.5y(1-x2)y(1-y)
на прямоугольной области определения x[-1,1], y[0,1].
>> [X,Y] = meshgrid(-1:0.05:1, 0:0.05:1);
>> Z = 4*sin(2*pi*X).*cos(1.5*pi*Y).*(1-X.^2).*Y.*(1-Y);
>> mesh(X,Y,Z)
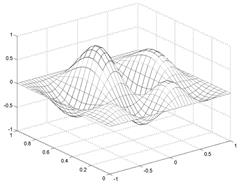
Рис. 1.5. Сетчатый 3D-график с функциональной окраской
Цвет линий соответствует значениям функции. MATLAB рисует только видимую часть поверхности. При помощи команды hidden off можно сделать каркасную модель «прозрачной», добавив скрытую часть. MATLAB имеет несколько функций, возвращающих матричный образ поверхностей. Например, функция peaks(N) возвращает матричный образ поверхности с рядом пиков и впадин. Такие функции удобно использовать для проверки команд трехмерной графики.
Пример:
>> z = peaks(25);
>> mesh(z)
1.5.4 Сетчатый 3D-график с функциональной окраской и проекцией
Иногда график поверхности полезно объединить с контурным графиком ее проекции на плоскость, расположенным под поверхностью.
meshc(…)
>> [X,Y] = meshgrid([-3:0.15:3]);
>> Z=X.^2+Y.^2;
>> meshc(X,Y,Z)
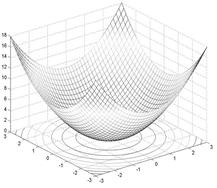
Рис. 1.6. Сетчатый 3D-график с функциональной окраской и проекцией
График такого типа дает лучшее представление об особенностях поверхности.
1.5.5 Поверхностный 3D-график с функциональной окраской
Наглядное представление о поверхностях дают графики, использующие функциональную закраску ячеек. Например, цвет окраски поверхности z(x,y) может быть поставлен в соответствие с высотой z поверхности с выбором для малых высот темных тонов, а для больших – светлых.
Для построения таких поверхностей используются команды класса surf(…).
surf(X,Y,Z,C) – строит цветную параметрическую поверхность по данным матриц X,Y и Z с цветом, задаваемым массивом C.
surf(X,Y,Z) – аналогична предшествующей команде, где C=Z.
Пример
>> [X,Y] = meshgrid([-3:0.15:3]);
>> Z=X.^2+Y.^2;
>> surf(X,Y,Z)
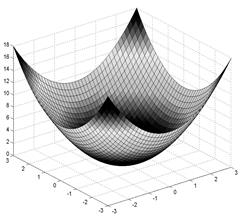
Рис. 1.7. Поверхностный 3D-график с функциональной окраской
>> colormap('') – задает окраску тонами определенного цвета
>> shading interp – обеспечивает устранение изображения сетки и задает интерполяцию для оттенков цвета объемной поверхности
Применение интерполяции для окраски придает поверхностям и фигурам более реалистичный вид, но фигуры каркасного вида дают более точные количественные данные о каждой точке.
1.5.6 Поверхностный 3D-график с функциональной окраской и освещением
Пожалуй, наиболее реалистичный вид имеют графики поверхностей, в которых имитируется освещение от точечного источника света, расположенного в заданном месте координатной системы. Графики имитируют оптические эффекты рассеивания, отражения и зеркального отражения света. Для получения таких эффектов используется команда surfl.
surfl(Z,S) или surfl(X,Y,Z,S) – строит графики поверхности с подсветкой от источника света, положение которого в системе декартовых координат задается вектором S=[Sx,Sy,Sz], а в системе сферических координат – вектором S=[AZ,EL];
При использовании surfl удобно задавать цветовые палитры: copper , bone, gray, pink, в которых интенсивность цвета изменяется линейно.
Пример.
>> [X,Y] = meshgrid(-1:0.05:1, 0:0.05:1);
>> Z = 4*sin(2*pi*X).*cos(1.5*pi*Y).*(1-X.^2).*Y.*(1-Y);
>> surfl(X,Y,Z)
>> colormap(‘copper’)
>> shading interp
По умолчанию источник света имеет азимут, больший на 45, чем наблюдатель, и тот же угол возвышения. Возможно изменение азимута источника. Например, изменим азимут до -90 по отношению к наблюдателю, а угол возвышения до нуля.
>> [Az , El] = view;
>> surfl(X,Y,Z,[Az-90,0])
>> shading interp
Азимут отсчитывается от оси, противоположной оси y, а угол возвышения - от плоскости xy.
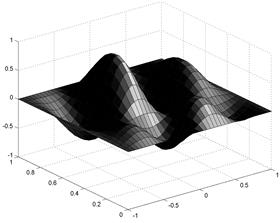
Рис. 1.8. Поверхностный 3D-график с функциональной окраской и освещением
Выполните задание к разделу 5: (задание 3 на стр. 26).
Дата: 2018-12-21, просмотров: 1090.