Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Выбор показателей качества

 

Необходимо выбрать показатели качества для программы контроля. Основными являются показатели, влияющие на эксплуатационные характеристики продукции или услуги. Они также могут относиться к аспектам предлагаемой услуги, признакам используемых материалов, деталям или узлам изделия, равно как и к готовому продукту, доставляемому покупателю. Статистичес­кие методы управления должны быть введены в первую очередь там, где контрольные карты будут помогать в сборе информации о процессе во времени, что позволит корректировать процесс и произ­водить лучшую продукцию или услугу. Показатели качества продукции или услуги должны быть выбраны таким образом, чтобы оказывать решающее влияние на их качество и обеспечить стабиль­ность процессов.

 

Анализ процесса производства

 

Детальный анализ процесса производства проводят для того, чтобы определить:

а)    вид и локализацию причин, которые могут возникнуть нерегулярно;

б)    влияние вводимых норм;

в)    методы и место контроля;

г)    все другие существенные факторы, которые могут влиять на процесс производства.

Анализ следует также проводить для определения стабильности производственных процессов, точности производственного и контрольного оборудования, качества производимой продукции или услуги и характера связи между типами и причинами несоответствий. Условия выполнения производ­ственных операций и обеспечения качества должны быть отрегулированы одновременно с корректи­ровкой производственного процесса и оборудования, а также с разработкой планов статистического управления процессами. Это поможет определить оптимальные места для размещения контроля, быстро выявить любую нерегулярность в ходе производственного процесса и обеспечить надлежащие коррек­тирующие действия.

 

Выбор рациональных подгрупп

В основе контрольных карт лежит идея Шухарта о разделении наблюдений на так называемые «рациональные» подгруппы, внутри которых могут возникнуть вариации, обусловленные только слу­чайными причинами, в то время как различия между ними могут быть обусловлены особыми причи­нами, которые контрольные карты и должны обнаружить.

 

11.4 Метод управления и интерпретации контрольных карт для количественных данных

 

Система карт Шухарта опирается на следующее условие: если изменчивость процесса от единицы к единице и среднее процесса остаются постоянными на данных уровнях (оцененные, соответственно, по 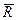 и X), то размахи R и средние  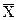отдельных подгрупп будут меняться только случайным образом и редко выходить за контрольные границы. Не допускаются очевидные тренды или структуры данных, кроме возникающих случайно с некоторой долей вероятности.  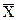-карта показывает, где находится среднее процесса и какова его стабильность. Та же карта выявляет нежелательные вариации между подгруппами и вариации относительно их среднего. R-карта выявляет любую нежелательную вариацию внутри подгрупп и служит индикатором изменчивости исследуемого процесса. Это мера состоятельности и однородности процесса. Если R-карта показывает, что вариации внутри подгрупп не изменяются, то это значит, что процесс остается в статистически управляемом состоянии. Такое происходит только в том случае, если все выборки обра­батывались одинаково. Если R-карта показывает, что процесс вышел из управляемого состояния или уровень на R-карте возрастает, то это может означать, что либо отдельные подгруппы подверглись разной обработке, либо в процессе действует несколько различных систем причинно-следственных связей.

На 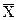 -карты также могут повлиять условия, при которых процесс вышел из состояния статис­тической управляемости по R-карте. Возможность интерпретировать размахи или средние подгрупп зависит от оценки изменчивости от единицы к единице, поэтому R-карту необходимо анализировать первой. Когда размахи находятся в статистически управляемом состоянии, разброс процесса (откло­нения внутри подгрупп) считается стабильным. В этом случае можно проанализировать средние, чтобы увидеть, меняется ли со временем среднее положение процесса.

Литература:

1 ГОСТ Р 50779.42 – 99 (ИСО 8258-91). Статистические методы. Контрольные карты Шухарта

ПОСТРОЕНИЕ КОНТРОЛЬНЫХ КАРТ СРЕДНИХ И РАЗМАХОВ (( 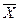- R)-карт)

План:

12.1 Построение контрольной карты средних и размахов

12.2 Чтение контрольной карты средних и размахов

Требования к технологическому процессу. Уровень несоответствий

Современная продукция, особенно сложные тех­нические изделия, состоит из сотен и даже тысяч эле­ментов, изготовляемых независимо. При этом несоот­ветствия по важным (ключевым) показателям качест­ва для компонентов или сборки приводят к тем или иным дефектам в готовой продукции. При этом вероятность (или доля) бездефектной продукции P_бездеф (по всем показателям) может быть рассчитана но формуле:

                             P_бездеф=(1-q₁)(1-q₂)….(1-q_k),                          (84)

где q₁ ....q_k — вероятности (доли) несоответствий, но отдельным ключевым показателям качества компо­нентов и операций сборки продукции.

Уровень несоответствий определяется в единицах ppm. Ppm – количество дефектных изделий на миллион.

Если вероятность (доля) несо­ответствий по каждому отдельному показателю состав­ляет всего 10 ppm (для большинства наших технологических процессов сегодня — это недостижимо), то при числе ключевых показателей 1000 получим

                              P_бездеф=1-(10 ppm ·1000)=1-0,01=0,99.

Таким образом, даже при таких «идеальных» технологических процессах мы уже будем иметь 1% дефектной продукции.

10 ppm - это малая величина, которая «неподвластна» контролю качества, ведь это всего 10 элементов с отклонением за пределы допуска на миллион выпушенных. Контроль, но принципу «годен — негоден», т. е.. по альтернативному признаку с участием человека «не чувствует» таких величин. Контролеры да­же при сплошном контроле будут пропускать несоот­ветствия из-за «потери бдительности». Необходимо организовать работу процессов так, чтобы они сами по себе обеспечива­ли эти «малые ppm». Для этого процесс должен обеспе­чивать относительно малый разброс показателя качест­ва, существенно меньший, чем ширина поля допуска. Но это возможно только при абсолютной стабильности процесса. Даже незначитель­ное отклонение технологического процесса по настройке может приводить к увеличению «вылетов» значений показателя качества за пределы допуска в десятки раз.

От процесса требуется следующее:

1. Процесс должен обеспечивать весьма малый есте­ственный разброс показателя качества, т. е. «присущий процессу» разброс должен быть достаточно мал, параметр σ должен быть не более 1/10 или в крайнем случае - 1/8 поля допуска. А центр настройки процесса (пара­метр 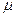) должен лежать в центре поля допуска или незначительно от него отстоять.

2. Процесс должен быть стабильным, т. е. нужно сделать так, чтобы 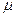  = const и σ = const. Только в этом случае не будет происходить неожиданного увели­чения несоответствий из-за отклонения  и при возрастании σ. А это значит, что необходимо выявить те факторы и причины, которые приводят к дестабилизации про­цесса.

Таким образом, необходимо экспериментально оп­ределить, какие факторы влияют на изменение центра на­стройки конкретного технологического процесса (т.е на изменение параметра 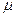) и какие - на изменение (увеличение) разброса процесса (т.е. на уве­личение параметра ).

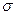Например, используя очень точное оборудование можно выявить влияние свойств сырья на входе процесса или технологиче­ских режимов на качество готовой продукции. При увеличении разброса показателей качества на выходе технологического процесса общее стандартное отклонение процесса увеличится, а значит, увеличатся и «вылеты» за гра­ницы допуска. Причиной этого является не само оборудование, а плохая организация процесса, т.е. внешние факторы, которые нужно найти и ликвидировать.

Очень многие количественно измеримые показатели при многократных измерениях достаточно точно могут быть описаны нормальным законом распределения. Это, например, та­кие показатели качества, как геометрические разме­ры, твердость, толщина покрытия и т. д. Отдельные значения данного показателя качества X разбросаны вокруг общего среднего значения 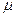, которое является фактическим центром настройки технологического процесса, а величина разброса индивидуальных значений X вокруг  характеризуется значением σ, которое является средней величиной отклонения од­ного значения X от . Таким образом,  отра­жает настройку (наладку) технологического процесса и является центральным фактиче­ским значением показателя X в текущее время работы технологического процесса, а σ отражает разброс технологического процесса, т. е. его «кучность». Чем меньше σ, тем меньше разброс, точки лежат «кучнее», т. е. тем выше технологическая точность.

В практических задачах точно определить  и σ невозможно, но можно по выборочным значе­ниям х₁, х₂, …. х_n (n — объем выборки) произвести оценки

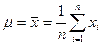                                               ^;                                                              (86)                                                                                                                                                

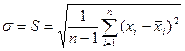                                                                   (87)

где 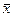 -функция выборочного среднего арифме­тического;

  S - функция выборочного среднего квадратического отклонения при неизвестном ^.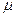

На рисунке 17 изображена плотность нормального рас­пределения (называемая «гауссовой кривой») W( x) и доли распределения в различных интервалах.Величина W(х) при разных значениях х показыва­ет, как «плотно», как «густо» лежат индивидуальные значения х в том или ином месте числовой осп. Пло­щадь под всей кривой W( x) равна единице, а площадь под W(х) внутри любого заданного интервала равна ве­роятности попадания или доле продукции внутри данно­го интервала (по показателю качества х).           

σ

                      

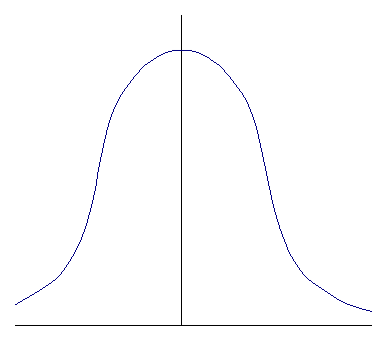
                                                    ± σ доля = 68,26 %

                                                   ± 2σ доля = 95,44 %

                                                      ± 3σ доля = 99,73 %

Рисунок 17 – Плотность нормального распределения

 

Как видно из рисунка 17, чем шире интервал по срав­нению с величиной σ, тем большая доля распределения будет попадать в этот интервал. Однако «хвосты» рас­пределения всегда выходят за границы интервала и резко убывают при увеличении числа «сигм».

Если указываемый интервал - это допуск на дан­ный показатель качества, а гауссова кривая с извест­ными или оцененными σ и  описывает поведение технологического процесса в данный период времени, то, как это очевидно из графического представления, можно вычислить (оценить, предсказать) долю соответствующей продукции и доли с завышенным и заниженным значениями показателя качества. Долю продукции в еди­ницах ppm за пределом одной из границ допуска мож­но оценить при помощи показателей (индексов) возможностей.

Для понимания статистической методологии и для практической работы с технологическими процессами важно, чтобы технологи, специалисты службы качества и другие сотрудники представляли поведение технологического процесса в текущий момент времени в виде гауссовой кривой. Важно также, чтобы специа­листы хорошо понимали (желательно, в количествен­ных оценках) зависимость долей несоответствующей продукции от величин параметров  и σ:

1) при смещении центра настройки технологического процесса ( 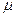) от центра поля допуска суммарный уровень несоответствий (сум­марная доля заниженных и завышенных значений) воз­растает.

2) при расширении гауссовой кривой (т. е. увеличении среднего разброса, увеличении σ) уровень несоот­ветствий по обе стороны допуска возрастает, поэтому важно обеспечить стабиль­ность технологического процесса по центру настройки и величине разброса.

Важно отмстить еще одно свойство нормального рас­пределения, касающееся выборочного среднего арифметического. Если из стабильного процесса с нормальным распределением W(х) берутся выборки постоянного  объема n и по каждой такой выборке вычисляется среднее арифметическое значение, то:

- выборочные средние арифметические значения 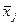 (j — номер выборки) являются случайными вели­чинами, распределенными по нормальному закону W( 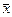) с параметрам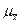и   и 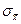, причем центр распределения W( 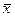) совпадает с цен­тром исходного распределении W(х), т. е.

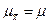                                        ,                                    (88)

- средние арифметические 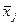 имеют разброс в  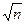раз меньший, чем отдельные выборочные значения 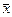, т. е.:

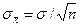                                       .                                    (89)

Соотношение распределений W(х) и W( 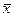) изображено на рисунке 18.

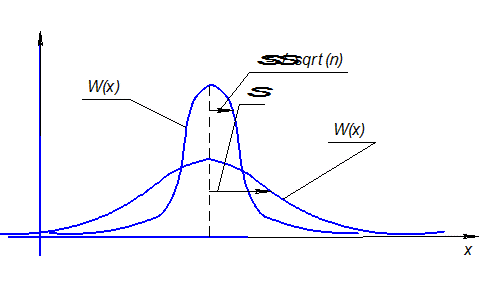
Рисунок 18 – Соотношение распределений W(х) и W( )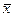

Отсюда следуют важные выводы:

- среднее арифметическое (даже по большой выборке) не является истинным центром настройки технологического процесса (центром распределения ), но дает возможность оценить 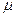 более точно, чем отдельные выборочные значения x_j.

Это свойство, в частности, интуитивно использует опытный наладчик станка-автомата: он делает несколько пробных деталей, вычисляет или оценивает «на глаз» среднее арифметическое, а затем корректирует настройку станка, учитывает отличие этого среднего от требуемого целевого значения настройки. Он делает так, потому, что знает из практики: по среднему настройка получается точнее, чем по индивидуальным значениям. Возможная погрешность будет в 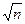 раз меньше, где n – число изготовленных пробных деталей;

- соотношение (89) позволяет определять необходимый объём выборки для заданной точности оценки , например, при настройке технологического процесса. Необходимо обеспечить, чтобы за время взятия этой выборки процесс оставался стабильным, т. е. чтобы было 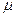=const; σ =const. Иначе увеличение n бессмысленно.

Следует отметить также, что даже если исходное распределение W( x) не совсем нормальное, то W( 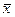) будет значительно ближе к нормальному, чем исходное. Это позволяет успешно применять контрольные карты Шухарта с несколькими выборками, даже если исходное распределение отличается от нормального.

 

Литература:

1. Пора заняться технологическим процессом [Текст] / М. И. Розно // Методы менеджмента качества. – 2004.- № 7. – С. 39-45

ЛЕКЦИЯ № 16 (4 ч)

Предварительный анализ состояния технологического процесса

При отклонении μ от заданного значения μ₀, а также при увели­чении σ увеличивается доля дефектной продукции р, что свиде­тельствует о разладке технологического процесса.

На стадии предварительного анализа состояния технологиче­ского процесса необходимо оценить параметры μ и σ. Для этого следует отобрать на контроль определенное количество единиц продукции. Чем большее число единиц продукции будет проконт­ролировано, тем более точной будет оценка этих параметров. Про­дукцию на контроль следует отбирать при нормальном ходе про­изводства, т. е. при надлежащем качестве сырья и при отлаженном оборудовании. При этих условиях получают оценки пара­метров μ и σ при налаженном состоянии технологического про­цесса, т. е.  μ₀ и σ₀. Зная эти значения, можно определить ве­роятную долю дефектной продукции р₀ при налаженном состоянии технологического процесса. Известно, что вся площадь под кривой нормального распреде­ления равна единице. Площадь под кривой между двумя предель­ными значениями Т_н и Т_в представляет собой ту долю всей сово­купности (принятой за единицу), для которой значения X лежат в пределах поля допуска, т. е. долю годной продукции q. Эта до­ля определяется как вероятность того, что случайная величина X примет значение в пределах Т_н - Т_в:

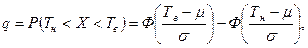                   ,              (90)

где Ф(Х)- функция нормального распределения. Доля дефект­ной продукции р=1 - q.

Из формулы (90) следует, что доля годной продукции q зави­сит от допуска, а также от значений μ и σ. Чем больше будет поле допуска, тем большей будет доля год­ной продукции, и наоборот, чем большим будет значение σ, тем меньшей будет доля годной продукции и тем большей будет доля дефектной продукции р. С дру­гой стороны, чем больше будет отклоняться μ от значения μ₀ (при неизменной σ) тем мень­шей будет доля годной про­дукции и тем большей будет доля дефектной продукции р.

Отсюда ясно, что при заданном допуске для уменьшения доли дефектной продукции р необходимо добиваться, чтобы, во-первых, значение μ не отклонялось от значения μ₀, которое обычно принимают равным середине допуска; во-вторых, чтобы значение σ не увеличивалось. Этого можно добиться путем своевременной подналадки оборудования.

При использовании формулы (90) в нее следует подставлять соответствующие значения μ₀ , μ₁ или σ₀, σ₁. Например, если мы хотим определить долю годной продукции при налаженном процессе, то в эту формулу следует подставить значения μ₀, σ₀; если же мы хотим определить долю годной продукции при разлаженном процессе, то в эту формулу следует подставить значения μ₁, σ₁.

Не менее важной характеристикой технологического процесса является его стабильность, заключающаяся в его способности со­хранять значения μ и σ неизменными в течение некоторого интер­вала времени без вмешательства извне. Ясно, что чем более ста­бильным будет технологический процесс, тем более редко будет происходить его разладка, которая приводит к приостановке про­цесса производства продукции для подналадки оборудования.

Таким образом, основная цель предварительного анализа со­стояния технологического процесса состоит в том, чтобы на осно­ве полученных результатов в случае необходимости привести про­цесс в статистически управляемое состояние.

ЛЕКЦИЯ № 17 (4 ч)

ЛЕКЦИЯ № 18 (2 ч)

Основы контрольных карт Шухарта

 

Задача статистического управления процессами — обеспечение и поддержание процессов на приемлемом и стабильном уровне, гарантируя соответствие продукции и услуг установленным требо­ваниям. Главный статистический инструмент, используемый для этого, — контрольная карта. Метод контрольных карт помогает определить, действительно ли процесс достиг статистически управляемого состояния на правильно заданном уровне или остается в этом состоянии, а затем поддерживать управление и высокую степень однородности важнейших харак­теристик продукции или услуги посредством непрерывной записи информации о качестве продукции в процессе производства. Использование контрольных карт и их тщательный анализ ведут к лучшему пониманию и совершенствованию процессов.

Контрольные карты Шухарта (ККШ) являются основным инструментом статистического управления качеством. ККШ применяют для сравнения получаемой по выборкам информации о текущем состоянии процесса с контрольными границами, представляющими пределы собственной изменчивости (разброса) процесса. ККШ используют для оценки того, находятся или не находятся производственный процесс, процесс обслуживания или административного управления в статистически управляемом состоянии. Первоначально ККШ были разработаны для применения в промышленном производстве. В настоящее время их широко используют в сфере обслуживания и других областях.

Контрольная карта – это графический способ представления и сопоставления информации, основанный на последовательности выборок, отражающих текущее состояние процесса, с границами, установленными на основе внутренне присущей процессу изменчивости.

Теория контрольных карт различает два вида изменчивости. Первый вид – изменчивость из-за «случайных (обычных величин), обусловленная бесчисленным набором разнообразных причин, присутствующих постоянно, которые нелегко или невозможно выявить. Каждая из таких причин составляет очень малую долю общей изменчивости, и не одна из них не значима сама по себе. Тем не менее, сумма всех этих причин измерима и предполагается, что она внутренне присуща процессу. Исключение или уменьшение влияния обычных причин требует управ­ленческих решений и выделения ресурсов на улучшение процесса и системы. Второй вид — реальные перемены в процессе. Они могут быть следствием некоторых определяе­мых причин, не присущих процессу внутренне, и могут быть устранены. Эти выявляемые причины рассматриваются как «неслучайные» или «особые» причины изменения. К ним могут быть отнесены поломка инструмента, недостаточная однородность материала, производ­ственного или контрольного оборудования, квалификация персонала, невыполнение процедур и т. д.

Цель контрольных карт — обнаружить неестественные изменения в данных из повторяющихся процессов и дать критерии для обнаружения отсутствия статистической управляемости. Процесс нахо­дится в статистически управляемом состоянии, если изменчивость вызвана только случайными причи­нами. При определении этого приемлемого уровня изменчивости любое отклонение от него считают результатом действия особых причин, которые следует выявить, исключить или ослабить.

Карта Шухарта требует данных, получаемых выборочно из процесса через примерно равные интервалы. Интервалы могут быть заданы либо по времени (например ежечасно), либо по количеству продукции (каждая партия). Обычно каждая подгруппа состоит из однотипных единиц продукции или услуг с одними и теми же контролируемыми показателями, и все подгруппы имеют равные объемы. Для каждой подгруппы определяют одну или несколько характеристик, таких как среднее арифметическое подгруппы 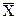 и размах подгруппы R или выборочное стандартное отклонение S. Карта Шухарта — это график значений определенных характеристик подгрупп в зависимости от их номеров. Она имеет центральную линию (CL), соответ­ствующую эталонному значению характеристики. При оценке того, находится ли процесс в статисти­чески управляемом состоянии, эталонным обычно служит среднее арифметическое рассматриваемых данных. При управлении процессом эталонным служит долговременное значение характеристики, ус­тановленное в технических условиях, или ее номинальное значение, основанное на предыдущей ин­формации о процессе, или намеченное целевое значение характеристики продукции или услуги. Карта Щухарта имеет две статистические определяемые контрольные границы относительно центральной линии, которые называются верхней контрольной границей (UCL) и нижней контрольной границей (LCL) (рисунок 9 ).

USL     CL   LCL

1              2             3                4              5             6 Порядковый номер выборки

 

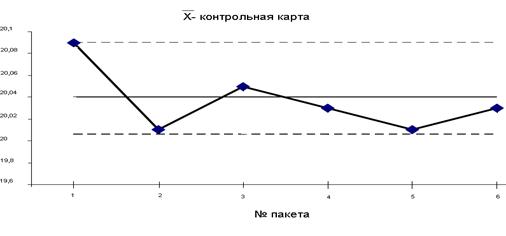
                      Рисунок 9 - Вид контрольной карты

Контрольные границы на карте Шухарта находятся на расстоянии З 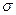 от центральной линии, где  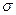— генеральное стандартное отклонение используемой статистики. Изменчивость внутри подгрупп является мерой случайных вариаций. Для получения оценки  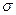вычисляют выборочное стандартное отклонение или умножают выборочный размах на соответствующий коэффициент. Эта мера не вклю­чает межгрупповых вариаций, а оценивает только изменчивость внутри подгрупп.

Границы ±3 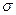 указывают, что около 99,7 % значений характеристики подгрупп попадут в эти пределы при условии, что процесс находится в статистически управляемом состоянии. Другими слова­ми, есть риск, равный 0,3 % (или в среднем три на тысячу случаев), что нанесенная точка окажется вне контрольных границ, когда процесс стабилен. Употребляется слово «приблизительно», поскольку отклонения от исходных предположений, таких как вид распределения данных, будут влиять на значения вероятности.

Некоторые консультанты предпочитают вместо множителя, равного 3, значение 3,09, чтобы обеспечить номинальное значение вероятности 0,2 % (в среднем два вводящих в заблуждение наблюде­ния на тысячу), но Шухарт выбрал число 3, чтобы не давать поводов к рассмотрению точных вероят­ностей. Аналогично некоторые консультанты применяют фактические значения вероятностей для карт, основанных на ненормальных распределениях, таких как карты размахов и долей несоответствий, и в этом случае в карте Шухарта также используют границы на расстоянии ± 3 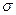 вместо вероятностных пределов, упрощая эмпирическую интерпретацию.

Вероятность того, что нарушение границ в самом деле случайное событие, а не реальный сигнал, считается столь малой, что при появлении точки вне границ следует предпринять определенные дей­ствия. Так как действие предпринимается именно в этой точке, то З 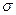 контрольные границы иногда называются «границами действий».

Часто на контрольной карте границы проводят еще и на расстоянии 2 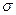. Тогда любое выборочное значение, попадающее за границы 2а, может служить предостережением о грозящей ситуации выхода процесса из состояния статистической управляемости. Поэтому границы ±2  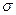иногда называют «пре­дупреждающими» .

При применении контрольных карт возможны два вида ошибок: первого и второго рода.

Ошибка первого рода возникает, когда процесс находится в статистически управляемом состоя­нии, а точка выскакивает за контрольные границы случайно. В результате неправильно решают, что процесс вышел из состояния статистической управляемости, и делают попытку найти и устранить причину несуществующей проблемы.

Ошибка второго рода возникает, когда рассматриваемый процесс не управляем, а точки случай­но оказываются внутри контрольных границ. В этом случае неверно заключают, что процесс статисти­чески управляем и упускают возможность предупредить рост выхода несоответствующей продукции. Риск ошибки второго рода - функция трех факторов: ширины контрольных границ, степени неуправ­ляемости и объема выборки. Их природа такова, что можно сделать лишь общее утверждение о величи­не ошибки.

Система карт Шухарта учитывает только ошибки первого рода, равные 0,3 % в пределах границ 3 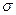. Поскольку в общем случае непрактично делать полную оценку потерь от ошибки второго рода в конкретной ситуации, а удобно произвольно брать малый объем подгруппы (4 или 5 единиц), целесо­образно использовать границы на расстоянии ± З  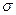и сосредоточивать внимание в основном на управле­нии и улучшении качества самого процесса.

Если процесс статистически управляем, контрольные карты реализуют метод непрерывной ста­тистической проверки нулевой гипотезы о том, что процесс не изменился и остается стабильным. Но поскольку значение конкретного отклонения характеристики процесса от цели, которое могло бы привлечь внимание, обычно нельзя определить заранее, как и риск ошибки второго рода, и объем выборки не рассчитывается для удовлетворения соответствующего уровня риска, то карту Шухарта не стоит рассматривать с точки зрения проверки гипотез. Шухарт подчеркивал именно эмпиричес­кую полезность контрольных карт для установления отклонений от состоянии статистической управ­ляемости, а не их вероятностную интерпретацию. Некоторые пользователи применяют кривые опера­тивных характеристик как средства для интерпретации проверок гипотез.

Когда наносимое значение выходит за любую из контрольных границ или серия значений прояв­ляет необычные структуры, состояние статистической управляемости подвергается сомне­нию. В этом случае надо исследовать и обнаружить неслучайные (особые) причины, а процесс можно остановить или скорректировать. Как только особые причины найдены и исключены, процесс снова готов к продолжению работы. При возникновении ошибки первого рода можно не найти никакой особой причины. Тогда считают, что выход точки за границы представляет собой достаточно редкое случайное явление при нахождении процесса в статистически управляемом состоянии.

Если контрольную карту процесса строят впервые, то часто оказывается, что процесс статисти­чески неуправляем. Контрольные границы, рассчитанные на основе данных такого процесса, будут иногда приводить к ошибочным заключениям, поскольку они могут оказаться слишком широкими. Следовательно, прежде чем устанавливать постоянные параметры контрольных карт, надо привести процесс в статистически управляемое состояние.