При статистическом регулировании технологических процессов приходится пе­риодически принимать решение - процесс налажен или процесс разлажен. Это решение принимается на основании результатов контроля единиц продукции в выборке. Таким образом, по выборке мы принимаем одну из двух гипотез - нулевую Н₀ - процесс налажен или альтернативную Н₁ - процесс разлажен.

Для решения подобных задач математическая статистика располагает теорией проверки статистических гипотез.

Применительно к задаче статистического регулирования ошибка первого рода состоит в том, что налаженный процесс будет принят за разлаженный и он будет необоснованно остановлен для корректировки, когда в этом нет необходимости. Ошибка второго рода в этой задаче состоит в том, что разлаженный процесс будет принят за налаженный, что приведет к выпуску бракованной продукции.

Вероятность совершить ошибку первого рода принято обозначать через α, а вероятность совершить ошибку второго рода - через β. Для задачи статистического регулирования α называется риском излишней наладки, β - риском незамеченной разладки. Критическими точками (границами) называют точки, отделяющие критическую область от интервала - области принятия гипотезы. Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области. Правосторонней называют критическую область, определяемую неравенством К>К_кр, где К - статистика критерия, К_кр - положительное число (рисунок 19 а). Левосторонней называют критическую область, определяемую неравенством К<К_кр, где К_кр — отрицательное число (рисунок 19 б). Двусторонней называют критическую область, определяемую неравенствами К<-К_кр, K> K_{к p},. В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется  неравенством 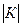>К_кр (рисунок 19 в).

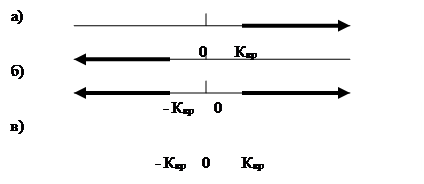Рисунок 19 – Область принятия гипотезы

Для отыскания правосторонней критической области, которая определяется неравенством К>К_кр, где К_кр,>0, достаточно найти критическую точку. С этой целью задаются достаточной малой вероятностью совершения ошибки первого рода - уровнем значимости α. Затем ищут критическую точку К_кр, исходя из требования, чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий К примет значение большее К_кр , была бы равна принятому уровню значимости

                                       Р (К>К_кр) = α.                                               (91)

Затем вычисляют по данным выборки частное значение критерия К_ч и, если окажется, что К_ч> К_кр, то нулевую гипотезу отвергают; если же К_ч< К_кр, то оснований отвергать нулевую гипотезу нет.

Отсюда ясно проглядывается схема простой контрольной карты. Если принять значение К_кр за ординату прямой, параллельной оси абсцисс, которую назовем границей регулирования, а ось абсцисс принять за исходную линию, соответствующую значению характеристики при налаженном процессе, то мы получим схему простой контрольной карты (рисунок 21).

Рисунок 21 – Схема простой контрольной карты

Границы регулирования ограничивают область допустимых значений выборочной статистики, где принимается нулевая гипотеза Н₀ - технологический процесс налажен. Область за границами регулирования является критической областью, где отвергается нулевая гипотеза и принимается альтернативная Н₁ - технологический процесс разлажен.

Мы строили критическую область исходя из требования, чтобы вероятность попадания в нее критерия К была равна α при условии, что нулевая гипотеза справедлива. Не менее важно знать также вероятность попадания критерия К в критическую область при условии, что нулевая гипотеза неверна и, следовательно, справедлива конкурирующая. Эта вероятность определяет мощность критерия.

Ясно, что чем меньше вероятности ошибок первого и второго рода, тем критическая область «лучше». Однако при заданном объеме выборки уменьшить одновременно α иβ невозможно. Если, например, уменьшить α, то β будет возрастать. Единственный способ одновременного уменьшения вероятностей ошибок первого и второго рода состоит в увеличении объема выборок. Если же объем выборки задан, то значения α иβ следует выбирать, учитывая «тяжесть» последствий ошибок для каждой конкретной задачи. Например, если риск незамеченной разладки β повлечет большие потери из-за увеличения доли дефектной продукции, а риск излишней наладки α повлечет существенно меньшие потери от необоснованной остановки процесса, то значение β следует выбирать возможно меньшим, невзирая на увеличение значения α.