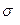Задача статистического регулирования технологическо­го процесса состоит в том, чтобы на основании результатов пери­одического контроля выборок малого объема принимать решение «процесс налажен» или «процесс разлажен». Поскольку разлад­ки технологического процесса происходят в случайные моменты времени и эти события подчиняются определенным статистиче­ским закономерностям, то такая задача решается методами мате­матической статистики. Рассмотрим простейшую схему такой за­дачи. Выдвигаются две гипотезы: нулевая гипотеза Но - техноло­гический процесс налажен, если параметр Ө распределения конт­ролируемого показателя качества X равен Ө ₀, и альтернативная гипотеза Н₁- технологический процесс разлажен, если параметр Ө равен Ө₁. В общем виде это записывается следующим образом:

Но: Ө = Ө ₀ (технологический процесс налажен);

Н₁: Ө = Ө₁ (технологический процесс разлажен).

На основании результатов контроля единиц продукции из выборки х₁, х₂,..., x_n можно с помощью определенных статисти­ческих критериев (о которых будет сказано далее) принять одну из этих двух гипотез.

Как мы помним, случайная величина X может быть непрерывной или дискретной. Например, диаметр отверстия представляет собой не­прерывную случайную величину, которая теоретически может при­нимать все значения в интервале, ограниченном допуском, скажем, между 34,5 и 35,5 мм. Практически эти значения ограничиваются определенной точностью измерительных средств. Непрерывную величину мы по­лучаем при контроле качества продукции по количественному при­знаку с помощью измерительных средств, позволяющих получить значение контролируемого параметра с большой точностью.

Дискретную величину мы получаем, например, при контроле качества продукции по альтернативному признаку, т. е. по при­знаку годен или не годен. В результате такого контроля мы под­считываем число дефектных единиц продукции или число дефек­тов. При этом нас не интересует истинное значение параметра X, достаточно лишь установить, соответствует ли оно установленно­му допуску, соответствует ли установленному образцу или нет.

Наиболее часто применяемым при решении задач статистиче­ского контроля качества распределением непрерывной случайной величины X является нормальное распределение .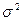

Как известно, нормаль­ное распределение определяется двумя параметрами: математи­ческим ожиданием µ и дисперсией .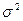

При статистическом регулировании технологических процессов при нормальном распределении случайной величины X проверяют гипотезы:

Н_о : μ = μ₀ (технологический процесс налажен);

H₁ : μ = μ₁ (технологический процесс разлажен),

если разладка связана с изменением математического ожидания μ.

Если же разладка связана с увеличением дисперсии σ², то в этом случае проверяют гипотезы:

Н₀ : σ = σ ₀ (технологический процесс налажен);

Н₁: σ = σ ₁ (технологический процесс разлажен).

При статистическом регулировании в качестве средних значе­ний обычно используют выборочное среднее арифметическое 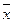 или выборочную медиану Ме, а в качестве меры рассеяния — выбороч­ное среднее квадратическое отклонение S или выборочную дисперсию S² или размах R.

При выборе между средним арифметическим и медианой, а также между средним квадратическим отклонением и размахом надо учитывать следующие соображения. Среднее арифмети­ческое является более эффективной статистикой, чем медиана (при нормальном распределении контролируемого параметра X), что позволяет при равных исходных условиях использовать объ­ем выборки примерно в полтора раза меньший. Точно также сред­нее квадратическое отклонение является более эффективной ста­тистикой, чем размах, что также позволяет использовать сущест­венно меньший объем выборки. Однако вычисление медианы и размаха проще среднего арифметического и среднего квадратического отклонений, поэтому первым двум статистикам иног­да отдают предпочтение.

В случае, когда контролируемым показателем качества явля­ется дискретная случайная величина, подчиняющаяся биномиаль­ному или пуассоновскому законам распределения, разладка про­цесса характеризуется увеличением доли дефектной продукции от значения р₀ до значения p₁. В этом случае проверяют гипотезы:

Н_о: р = р₀ (технологический процесс налажен);

Н₁:р = р₁ (технологический процесс разлажен).

Технологический процесс должен обеспечивать на выходе продукцию, полностью соответствующую всем требованиям, т. е. с показателями качества, значения которых лежат внутри установленных для них допусков. «Вылет» за пределы допуска не допустим, это - брак.

При серийном и массовом производстве, как известно, для множества однотипных изделий по каждому по­казателю качества можно построить гистограмму и распределение, например, нормальное. «Хвосты» распределения всегда выходят за пределы допуска, показывая, что образуется брак. Вероятность появления брака всегда можно вычислить с помощью функции нормального распределения.

Требования к технологическому процессу. Уровень несоответствий

Современная продукция, особенно сложные тех­нические изделия, состоит из сотен и даже тысяч эле­ментов, изготовляемых независимо. При этом несоот­ветствия по важным (ключевым) показателям качест­ва для компонентов или сборки приводят к тем или иным дефектам в готовой продукции. При этом вероятность (или доля) бездефектной продукции P_бездеф (по всем показателям) может быть рассчитана но формуле:

                             P_бездеф=(1-q₁)(1-q₂)….(1-q_k),                          (84)

где q₁ ....q_k — вероятности (доли) несоответствий, но отдельным ключевым показателям качества компо­нентов и операций сборки продукции.

Уровень несоответствий определяется в единицах ppm. Ppm – количество дефектных изделий на миллион.

Если вероятность (доля) несо­ответствий по каждому отдельному показателю состав­ляет всего 10 ppm (для большинства наших технологических процессов сегодня — это недостижимо), то при числе ключевых показателей 1000 получим

                              P_бездеф=1-(10 ppm ·1000)=1-0,01=0,99.

Таким образом, даже при таких «идеальных» технологических процессах мы уже будем иметь 1% дефектной продукции.

10 ppm - это малая величина, которая «неподвластна» контролю качества, ведь это всего 10 элементов с отклонением за пределы допуска на миллион выпушенных. Контроль, но принципу «годен — негоден», т. е.. по альтернативному признаку с участием человека «не чувствует» таких величин. Контролеры да­же при сплошном контроле будут пропускать несоот­ветствия из-за «потери бдительности». Необходимо организовать работу процессов так, чтобы они сами по себе обеспечива­ли эти «малые ppm». Для этого процесс должен обеспе­чивать относительно малый разброс показателя качест­ва, существенно меньший, чем ширина поля допуска. Но это возможно только при абсолютной стабильности процесса. Даже незначитель­ное отклонение технологического процесса по настройке может приводить к увеличению «вылетов» значений показателя качества за пределы допуска в десятки раз.

От процесса требуется следующее:

1. Процесс должен обеспечивать весьма малый есте­ственный разброс показателя качества, т. е. «присущий процессу» разброс должен быть достаточно мал, параметр σ должен быть не более 1/10 или в крайнем случае - 1/8 поля допуска. А центр настройки процесса (пара­метр 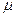) должен лежать в центре поля допуска или незначительно от него отстоять.

2. Процесс должен быть стабильным, т. е. нужно сделать так, чтобы 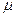  = const и σ = const. Только в этом случае не будет происходить неожиданного увели­чения несоответствий из-за отклонения  и при возрастании σ. А это значит, что необходимо выявить те факторы и причины, которые приводят к дестабилизации про­цесса.

Таким образом, необходимо экспериментально оп­ределить, какие факторы влияют на изменение центра на­стройки конкретного технологического процесса (т.е на изменение параметра 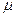) и какие - на изменение (увеличение) разброса процесса (т.е. на уве­личение параметра ).

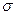Например, используя очень точное оборудование можно выявить влияние свойств сырья на входе процесса или технологиче­ских режимов на качество готовой продукции. При увеличении разброса показателей качества на выходе технологического процесса общее стандартное отклонение процесса увеличится, а значит, увеличатся и «вылеты» за гра­ницы допуска. Причиной этого является не само оборудование, а плохая организация процесса, т.е. внешние факторы, которые нужно найти и ликвидировать.

Очень многие количественно измеримые показатели при многократных измерениях достаточно точно могут быть описаны нормальным законом распределения. Это, например, та­кие показатели качества, как геометрические разме­ры, твердость, толщина покрытия и т. д. Отдельные значения данного показателя качества X разбросаны вокруг общего среднего значения 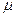, которое является фактическим центром настройки технологического процесса, а величина разброса индивидуальных значений X вокруг  характеризуется значением σ, которое является средней величиной отклонения од­ного значения X от . Таким образом,  отра­жает настройку (наладку) технологического процесса и является центральным фактиче­ским значением показателя X в текущее время работы технологического процесса, а σ отражает разброс технологического процесса, т. е. его «кучность». Чем меньше σ, тем меньше разброс, точки лежат «кучнее», т. е. тем выше технологическая точность.

В практических задачах точно определить  и σ невозможно, но можно по выборочным значе­ниям х₁, х₂, …. х_n (n — объем выборки) произвести оценки

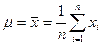                                               ^;                                                              (86)                                                                                                                                                

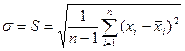                                                                   (87)

где 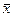 -функция выборочного среднего арифме­тического;

  S - функция выборочного среднего квадратического отклонения при неизвестном ^.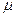

На рисунке 17 изображена плотность нормального рас­пределения (называемая «гауссовой кривой») W( x) и доли распределения в различных интервалах.Величина W(х) при разных значениях х показыва­ет, как «плотно», как «густо» лежат индивидуальные значения х в том или ином месте числовой осп. Пло­щадь под всей кривой W( x) равна единице, а площадь под W(х) внутри любого заданного интервала равна ве­роятности попадания или доле продукции внутри данно­го интервала (по показателю качества х).           

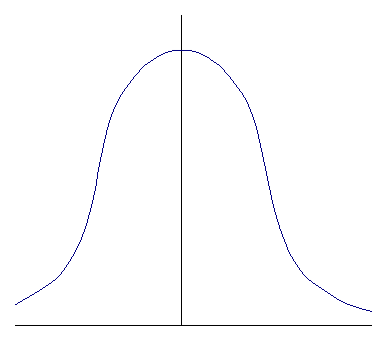
                                                    ± σ доля = 68,26 %

                                                   ± 2σ доля = 95,44 %

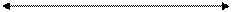                                                      ± 3σ доля = 99,73 %

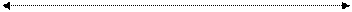Рисунок 17 – Плотность нормального распределения

Как видно из рисунка 17, чем шире интервал по срав­нению с величиной σ, тем большая доля распределения будет попадать в этот интервал. Однако «хвосты» рас­пределения всегда выходят за границы интервала и резко убывают при увеличении числа «сигм».

Если указываемый интервал - это допуск на дан­ный показатель качества, а гауссова кривая с извест­ными или оцененными σ и  описывает поведение технологического процесса в данный период времени, то, как это очевидно из графического представления, можно вычислить (оценить, предсказать) долю соответствующей продукции и доли с завышенным и заниженным значениями показателя качества. Долю продукции в еди­ницах ppm за пределом одной из границ допуска мож­но оценить при помощи показателей (индексов) возможностей.

Для понимания статистической методологии и для практической работы с технологическими процессами важно, чтобы технологи, специалисты службы качества и другие сотрудники представляли поведение технологического процесса в текущий момент времени в виде гауссовой кривой. Важно также, чтобы специа­листы хорошо понимали (желательно, в количествен­ных оценках) зависимость долей несоответствующей продукции от величин параметров  и σ:

1) при смещении центра настройки технологического процесса ( 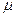) от центра поля допуска суммарный уровень несоответствий (сум­марная доля заниженных и завышенных значений) воз­растает.

2) при расширении гауссовой кривой (т. е. увеличении среднего разброса, увеличении σ) уровень несоот­ветствий по обе стороны допуска возрастает, поэтому важно обеспечить стабиль­ность технологического процесса по центру настройки и величине разброса.

Важно отмстить еще одно свойство нормального рас­пределения, касающееся выборочного среднего арифметического. Если из стабильного процесса с нормальным распределением W(х) берутся выборки постоянного  объема n и по каждой такой выборке вычисляется среднее арифметическое значение, то:

- выборочные средние арифметические значения 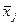 (j — номер выборки) являются случайными вели­чинами, распределенными по нормальному закону W( 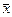) с параметрам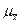и   и 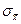, причем центр распределения W( 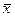) совпадает с цен­тром исходного распределении W(х), т. е.

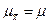                                        ,                                    (88)

- средние арифметические 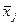 имеют разброс в  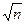раз меньший, чем отдельные выборочные значения 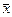, т. е.:

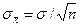                                       .                                    (89)

Соотношение распределений W(х) и W( 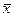) изображено на рисунке 18.

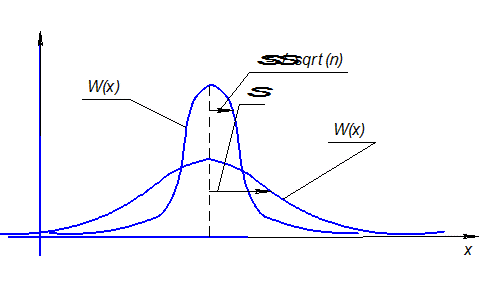
Рисунок 18 – Соотношение распределений W(х) и W( )

Отсюда следуют важные выводы:

- среднее арифметическое (даже по большой выборке) не является истинным центром настройки технологического процесса (центром распределения ), но дает возможность оценить  более точно, чем отдельные выборочные значения x_j.

Это свойство, в частности, интуитивно использует опытный наладчик станка-автомата: он делает несколько пробных деталей, вычисляет или оценивает «на глаз» среднее арифметическое, а затем корректирует настройку станка, учитывает отличие этого среднего от требуемого целевого значения настройки. Он делает так, потому, что знает из практики: по среднему настройка получается точнее, чем по индивидуальным значениям. Возможная погрешность будет в  раз меньше, где n – число изготовленных пробных деталей;

- соотношение (89) позволяет определять необходимый объём выборки для заданной точности оценки , например, при настройке технологического процесса. Необходимо обеспечить, чтобы за время взятия этой выборки процесс оставался стабильным, т. е. чтобы было 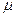=const; σ =const. Иначе увеличение n бессмысленно.

Следует отметить также, что даже если исходное распределение W( x) не совсем нормальное, то W( 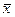) будет значительно ближе к нормальному, чем исходное. Это позволяет успешно применять контрольные карты Шухарта с несколькими выборками, даже если исходное распределение отличается от нормального.

Литература:

1. Пора заняться технологическим процессом [Текст] / М. И. Розно // Методы менеджмента качества. – 2004.- № 7. – С. 39-45

ЛЕКЦИЯ № 16 (4 ч)