Пусть собственные средства банка вместе с депозитами в сумме составляют 100 млн. долл. Часть этих средств, но не менее 35 млн. долл., должна быть размещена в кредитах, ценные бумаги должны составлять не менее 30% средств, размещенных в кредитах и ценных бумагах. Доходность кредитов – 6% годовых, доходность ценных бумаг – 3% годовых. Найти такое соотношение средств, размещенных в кредитах и ценных бумагах, чтобы максимизировать общий доход банка.
Математическая постановка задачи:
Переменные:
Х1 – средства (в млн. долл.), размещенные в кредитах;
Х2 – средства (в млн. долл.), размещенные в ценных бумагах.
Целевая функция:
f(x) = 0,06*X1 + 0,03*X2 ® mах
Ограничения:
Х1, Х2 ³ 0;
Х1 + Х2 £ 100 – балансовое ограничение;
Х1 ³ 35 – кредитное ограничение;
Х2 ³ 0,3 * (Х1 + Х2) – ликвидное ограничение.
Задачу предлагается решить самостоятельно, используя навыки полученные при решении предыдущей задачи.
Задача оптимального использования ресурсов
Фабрика имеет в своем распоряжении определенное количество ресурсов: рабочую силу, денежные средства, сырье, оборудование и может выпускать товары четырех видов. Исходные данные для решения задачи приведены в таблице 4.2.
Таблица 4.2 - Исходные данные задачи
| Ресурсы | нормы расхода на единицу товара | наличие ресурсов | |||
| товар 1 | товар 2 | товар 3 | товар 4 | ||
| Труд (чел/дней) | 7 | 2 | 2 | 6 | 80 |
| Сырье (кг) | 5 | 8 | 4 | 3 | 480 |
| Оборудование (станко/ч) | 2 | 4 | 1 | 8 | 130 |
| Цена (тыс. руб.) | 3 | 4 | 3 | 1 | |
Требуется найти такой план выпуска продукции, при котором общая стоимость продукции была максимальной.
Математическая постановка задачи:
Переменные:
Х1, Х2, Х3, Х4 – количество товаров каждого вида.
Целевая функция:
f(x) = 3*X1 + 4*X2 +3*Х3 + Х4 ® mах
Ограничения:
Х1, Х2, Х3, Х4 ³ 0;
7*X1 + 2*X2 +2*Х3 + 6*Х4 £ 80 ;
5*X1 + 8*X2 +4*Х3 + 3*Х4 £ 480 ;
2*X1 + 4*X2 + Х3 + 8*Х4 £ 130 ;
Задачу предлагается решить самостоятельно, используя навыки, полученные при решении предыдущих задач.
Транспортная задача
Дано 5 производителей А1, А2, А3, А4, А5, мощность (запасы) которых соответственно равна(равны): 20, 45, 25, 30,20. И четыре потребителя В1, В2, В3, В4, потребность которых в продукте составляет соответственно: 45, 50, 20, 25.
Также известна матрица издержек Сij – издержки перевозки единицы груза от i-ого поставщика к j-ому потребителю.
Ее можно представить таблицей:
| 12 | 9 | 10 | 4 |
| 4 | 7 | 7 | 6 |
| 7 | 11 | 5 | 8 |
| 9 | 6 | 9 | 9 |
| 10 | 11 | 6 | 5 |
Полностью, условие транспортной задачи, можно представить таблицей следующего содержания:
| 45 | 50 | 20 | 25 | |
| 20 | 12 | 9 | 10 | 4 |
| 45 | 4 | 7 | 7 | 6 |
| 25 | 7 | 11 | 5 | 8 |
| 30 | 9 | 6 | 9 | 9 |
| 20 | 10 | 11 | 6 | 5 |
Решение:
Введите исходные данные, начиная с ячейки А1
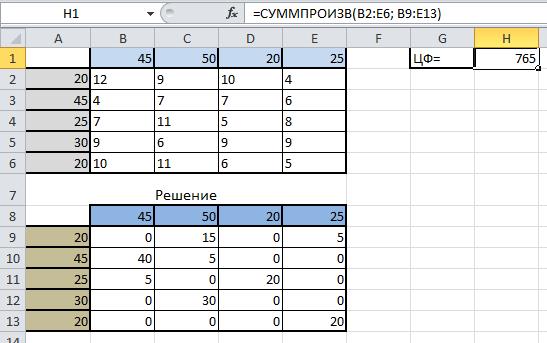
В ячейку Н1 введите формулу: СУММПРОИЗВ(В2:E6;B9:E13)
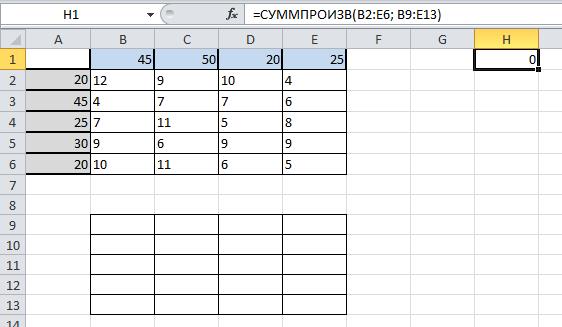
В ячейку A9 введите формулу СУММ(B9:Е9) и растяните её до А13
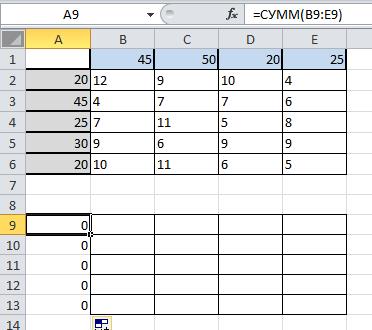
В ячейку B8 введите формулу СУММ(B9:B13) и скопируйте ее в диапазон от B8 до E8:
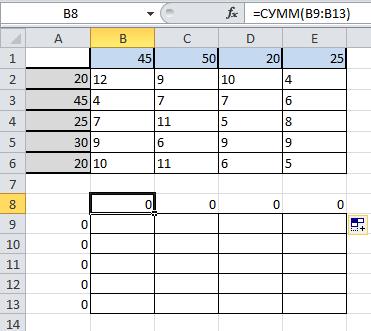
Для решения задачи на панели вкладок выберите вкладку «Данные», а затем «Поиск решения»:

Заполните открывшееся окно в соответствие с рисунком и нажмите Найти решение:
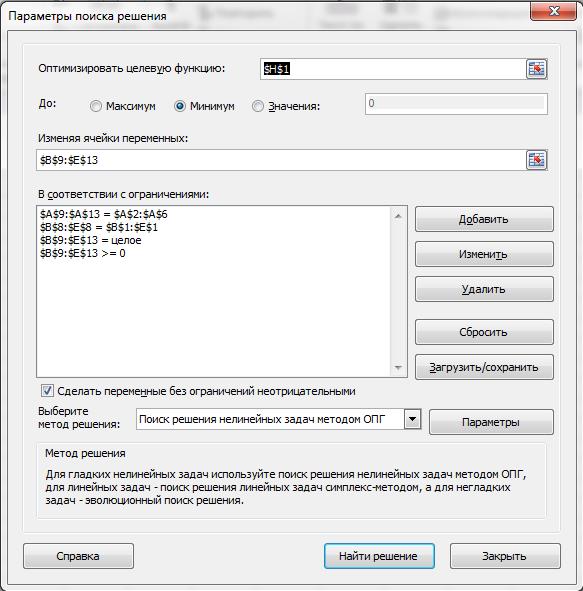
В диапазоне B9:E13 Вы получите результат решения транспортной задачи (т.е. значение в ячейке соответствует количеству груза перевезенного от i-ого поставщика к j-ому потребителю).
В диапазоне A9:A13 количество груза, которое необходимо вывезти от поставщиков.
В диапазоне B8:E8 количество которое будет доставлено потребителям согласно найденному решению.
В ячейке H1 значение целевой функции при найденном решении (минимально возможное - 765). Это значение получено в результате умножения стоимости перевозки от от i-ого поставщика к j-ому потребителю на количество единиц груза, которые необходимо перевезти между ними.
Оформим полученный результат и получим следующее:
Задания для самостоятельного выполнения.
1.Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуются 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй моделей равна $30 и $20 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.
2. Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках (таблица 4.3). Время использования этих станков для производства данных изделий ограничено 10 ч в сутки. Найти оптимальный объем производства изделий каждого вида.
Таблица 4.3 – Исходные данные по задаче
| Изделие | Время обработки одного изделия, мин | Удельная прибыль, $ | |||
| Станок 1 | Станок 2 | Станок 3 | |||
| 1 | 10 | 6 | 8 | 2 | |
| 2 | 5 | 20 | 15 | 3 | |
3. Фирма производит два вида продукции – А и В. Объем сбыта продукции вида А составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 кг. Расход сырья на единицу продукции А составляет 2 кг, а на единицу продукции В – 4 кг. Цены продукции А и В равны $20 и $40 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.
4. Фирма выпускает ковбойские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $8, а фасона 2 – $5. Определить, какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.
5. Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков приведено в таблице 4.4.
Таблица 4.4 – Исходные данные для задачи
Станок
Дата: 2018-11-18, просмотров: 714.