В анализе стохастических процессов важное значение имеют статистические взаимосвязи между случайными величинами. В предыдущем примере для установления степени взаимосвязи ключевых и расчетных показателей мы использовали графический анализ. В качестве количественных характеристик подобных взаимосвязей в статистике используют два показателя: ковариацию и корреляцию.
Ковариация и корреляция
Ковариация выражает степень статистической зависимости между двумя множествами данных и определяется из следующего соотношения:
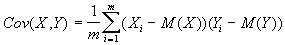
где X, Y - множества значений случайных величин размерности m; M(X) - математическое ожидание случайной величины Х; M(Y) - математическое ожидание случайной величины Y.
Как следует из формулы, положительная ковариация наблюдается в том случае, когда большим значениям случайной величины Х соответствуют большие значения случайной величины Y, т.е. между ними существует тесная прямая взаимосвязь. Соответственно отрицательная ковариация будет иметь место при соответствии малым значениям случайной величины Х больших значений случайной величины Y. При слабо выраженной зависимости значение показателя ковариации близко к 0.
Ковариация зависит от единиц измерения исследуемых величин, что ограничивает ее применение на практике. Более удобным для использования в анализе является производный от нее показатель - коэффициент корреляции R, вычисляемый по формуле:
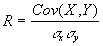
Коэффициент корреляции обладает теми же свойствами, что и ковариация, однако является безразмерной величиной и принимает значения от -1 (характеризует линейную обратную взаимосвязь) до +1 (характеризует линейную прямую взаимосвязь). Для независимых случайных величин значение коэффициента корреляции близко к 0.
Определение количественных характеристик для оценки тесноты взаимосвязи между случайными величинами в ППП EXCEL может быть осуществлено двумя способами:
- с помощью статистических функций КОВАР() и КОРРЕЛ();
- с помощью специальных инструментов статистического анализа.
Если число исследуемых переменных больше 2, более удобным является использование инструментов анализа.
Инструмент анализа данных "Корреляция"
Определим степень тесноты взаимосвязей между переменными V, Q, P, NCF и NPV. При этом в качестве меры будем использовать показатель корреляции R.
1. Выберите "Анализ данных". Выберите из списка "Инструменты анализа" пункт "Корреляция" и нажмите кнопку "ОК" (рисунок 3.1). Результатом будет появление окна диалога инструмента "Корреляция".
2. Заполните поля диалогового окна, как показано на рисунке 3.2.
Вид полученной ЭТ после выполнения элементарных операций форматирования приведен на рисунке 3.3.
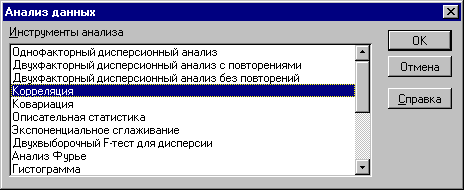
Рис.3.1. Список инструментов анализа (выбор пункта "Корреляция")
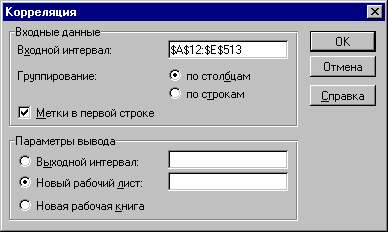
Рис.3.2. Заполнение окна диалога инструмента "Корреляция"
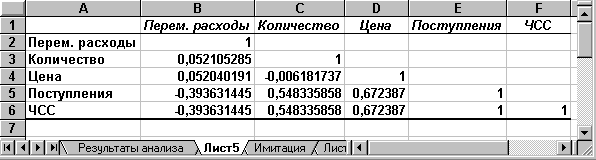
Рис. 3.3. Результаты корреляционного анализа
Результаты корреляционного анализа представлены в ЭТ в виде квадратной матрицы, заполненной только наполовину, поскольку значение коэффициента корреляции между двумя случайными величинами не зависит от порядка их обработки. Нетрудно заметить, что эта матрица симметрична относительно главной диагонали, элементы которой равны 1, так как каждая переменная коррелирует сама с собой.
Как следует из результатов корреляционного анализа, выдвинутая в процессе решения предыдущего примера гипотеза о независимости распределений ключевых переменных V, Q, P в целом подтвердилась. Значения коэффициентов корреляции между переменными расходами V, количеством Q и ценой Р (ячейки В3:В4, С4) достаточно близки к 0.
В свою очередь величина показателя NPV напрямую зависит от величины потока платежей (R = 1). Кроме того, существует корреляционная зависимость средней степени между Q и NPV (R = 0,548), P и NPV (R = 0,67). Как и следовало ожидать, между величинами V и NPV существует умеренная обратная корреляционная зависимость (R = -0,39).
Полезность проведения последующего статистического анализа результатов имитационного эксперимента заключается также в том, что во многих случаях он позволяет выявить некорректности в исходных данных, либо даже ошибки в постановке задачи. В частности в рассматриваемом примере, отсутствие взаимосвязи между переменными затратами V и объемами выпуска продукта Q требует дополнительных объяснений, так как с увеличением последнего, величина V также должна расти . Таким образом, установленный диапазон изменений переменных затрат V нуждается в дополнительной проверке и, возможно, корректировке.
Следует отметить, что близкие к нулевым значения коэффициента корреляции R указывают на отсутствие линейной связи между исследуемыми переменными, но не исключают возможности нелинейной зависимости. Кроме того, высокая корреляция не обязательно всегда означает наличие причинной связи, так как две исследуемые переменные могут зависеть от значений третьей.
При проведении имитационного эксперимента и последующего вероятностного анализа полученных результатов мы исходили из предположения о нормальном распределении исходных и выходных показателей. Вместе с тем, справедливость сделанных допущений, по крайней мере для выходного показателя NPV, нуждается в проверке.
Для проверки гипотезы о нормальном распределении случайной величины применяются специальные статистические критерии: Колмогорова-Смирнова, c 2. В целом ППП EXCEL позволяет быстро и эффективно осуществить расчет требуемого критерия и провести статистическую оценку гипотез.
Теоретический материал и инструкции по применению программного средства [3]
Одной из распространенных задач в науке, технике, экономике является аппроксимация численных эмпирических данных аналитическими выражениями. Возможность подобрать параметры уравнения таким образом, чтобы его решение совпало с данными эксперимента, зачастую является доказательством (или опровержением) теории.
Рассмотрим следующую математическую задачу. Известные значения некоторой функции f образуют таблицу 3.1:
| Таблица 3.1 Значение фунции | ||||
| X | x1 | x2 | . . . | xn |
| f(x) | y1 | y2 | . . . | yn |
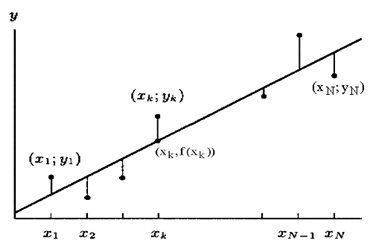
Необходимо построить аналитическую зависимость y = f(x), наиболее близко описывающую результаты эксперимента. Построим функцию y = f(x, a0, a1, ..., ak) таким образом, чтобы сумма квадратов отклонений измеренных значений yi от расчетных f(xi ,a0, a1, ..., ak) была наименьшей (см. рис. 3.1).
|
| Рис. 3.1 График функции |
Математически эта задача равносильна следующей: найти значение параметров a0, a1, a2, ...,ak, при которых функция принимала бы минимальное значение (формула 3.1).
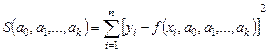 (3.1)
(3.1)
Эта задача сводится к решению системы уравнений (3.2):
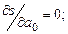
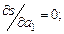
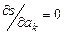 (3.2)
(3.2)
Если параметры ai входят в зависимость y = f(x,ao, a1, …, ak) линейно, то мы получим систему линейных уравнений (3.3):
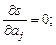
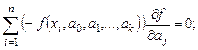
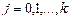 (3.3)
(3.3)
Решив систему (3.3), найдем параметры ao, a1, ..., ak и получим зависимость y = f(x, ao, a1, ..., ak).
Дата: 2018-11-18, просмотров: 434.