Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Статистическая обработка данных и имитационное моделирование в среде табличного процессора Excel

 

 

 

 

Методические указания к лабораторным работам

для магистров экономического факультета специальности

080200 – Менеджмент

 

Калининград, 2012

 

 

 

Оглавление

Введение. 3

Лабораторная работа № 1. 4

Моделирование риска инвестиционного проекта с использованием.. 4

встроенных функций ППП MS Excel 2007. 4

Лабораторная работа № 2. 19

Моделирование риска инвестиционного проекта с использованием.. 19

инструмента «Генератор случайных чисел» MS Excel 19

Лабораторная работа № 3. 31

Статистический анализ результатов имитационного эксперимента. 31

Лабораторная работа № 4. 41

Оптимизационный анализ в МS Excel 41

Лабораторная работа № 5. 48

Прогнозирование данных в MS Excel 48

Лабораторная работа № 6. 52

Зачетное задание. 52

Список литературы.. 56

 

 

Введение

 

Данное пособие с лабораторным практикумом предназначено для студентов специальности 0802000 – «Менеджмент », изучающих дисциплину «Информационные технологии в менеджменте». Выбор программного продукта MS Excel 2007 обусловлен двумя причинами. Во-первых, данная программа является наиболее мощным и гибким средством обработки больших объемов цифровых данных со встроенными механизмами финансового и статистического анализа. Полученные в ходе выполнения лабораторных работ навыки будут в дальнейшем использованы магистрантами при подготовке выпускных магистерских диссертаций. Во-вторых, данный программный продукт очень широко распространен и доступен, поэтому каждый студент может успешно использовать его в дальнейшей профессиональной деятельности.

Пособие состоит из пяти лабораторных работ. В начале каждой работы приводятся краткие теоретические сведения, необходимые для выполнения работы. Далее описывается технология выполнения работы. Также для каждой работы предусмотрено конкретное задание по вариантам. Предложения, помеченные цифрами в тексте пособия, студент должен выполнять. Рассматриваемый перечень лабораторных работ может быть выполнен в течение одного семестра.

Лабораторные работы выполняются в компьютерных классах университета. Студентам рекомендуется иметь устройство для сохранения выполненных работ, т. к. задания в некоторых лабораторных работах предполагают использование результатов предыдущих работ.

При подготовке лабораторного практикума использованы некоторые примеры из литературы приведённого списка.  

 

 

 

Лабораторная работа № 1

Моделирование риска инвестиционного проекта с использованием

Функция НОРМСТРАСП(Z)

Эта функция возвращает стандартное нормальное распределение, т.е. вероятность того, что случайная нормализованная величина Е будет меньше или равна х. Она имеет всего один аргумент - Z, вычисляемый функцией НОРМАЛИЗАЦИЯ().

Нетрудно заметить, что эти функции следует использовать вместе. При этом наиболее эффективным и компактным способом их задания является указание функции НОРМАЛИЗАЦИЯ() в качестве аргумента функции - НОРМСТРАСП(), т.е.:

=НОРМСТРАСП(НОРМАЛИЗАЦИЯ(x; среднее; станд_откл)).

С целью повышения наглядности, в проектируемом шаблоне функции заданы раздельно (ячейки Е18 и F18).

Сформируйте данный шаблон и сохраните его на магнитном диске под именем SIMUL_1. Приступаем к имитационному эксперименту. Для его проведения необходимо выполнить следующие шаги.

1. Ввести значения постоянных переменных (табл. 1.2) в ячейки В2:В4 и D2:D4 листа "Результаты анализа".

2. Ввести значения диапазонов изменений ключевых переменных (табл.  1.1) в ячейки В3:С5 листа "Имитация".

3. Нажатием клавиши F9 провести расчет.

4.  Перейти к листу "Результаты анализа" и проанализировать полученные результаты.

Результатом выполнения этих действий будет заполнение блока А10:Е510 случайными значениями ключевых переменных V, Q, P и результатами вычислений величин NCF и NPV. Фрагмент результатов имитации приведен на рис. 1.3.  Соответствующие проведенному эксперименту результаты анализа приведены на рисунке 1.4.

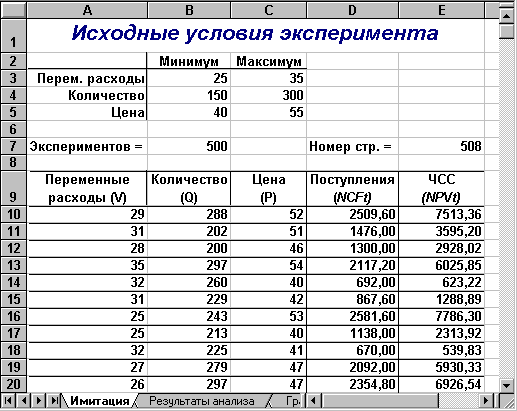
Рис. 1.3- Результаты имитации

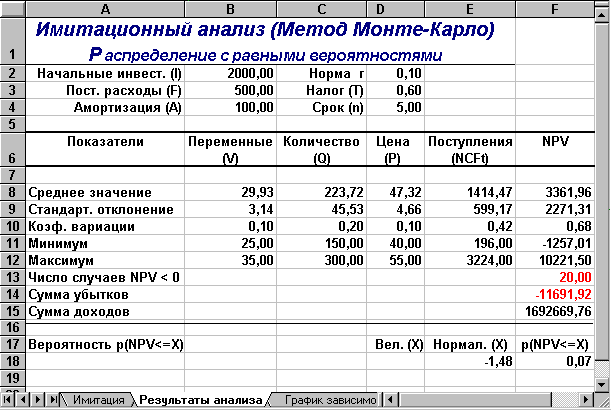
Рис. 1.4 - Результаты анализа

    Сумма всех отрицательных значений NPV в полученной генеральной совокупности (ячейка F14) может быть интерпретирована как чистая стоимость неопределенности для инвестора в случае принятия проекта. Аналогично сумма всех положительных значений NPV (ячейка F15) может трактоваться как чистая стоимость неопределенности для инвестора в случае отклонения проекта. Несмотря на всю условность этих показателей, в целом они представляют собой индикаторы целесообразности проведения дальнейшего анализа.

В данном случае они наглядно демонстрируют несоизмеримость суммы возможных убытков по отношению к общей сумме доходов (-11691,92 и 1692669,76 соответственно).

На практике одним из важнейших этапов анализа результатов имитационного эксперимента является исследование зависимостей между ключевыми параметрами. Ограничимся визуальным (графическим) исследованием. На рисунке 1.5 приведен график распределения значений ключевых параметров V, P и Q, построенный на основании 75 имитаций.

Нетрудно заметить, что в целом, вариация значений всех трех параметров носит случайный характер, что подтверждает принятую ранее гипотезу об их независимости. Для сравнения ниже приведен график распределений потока платежей NCF и величины NPV (рисунок 1.6).

 

 

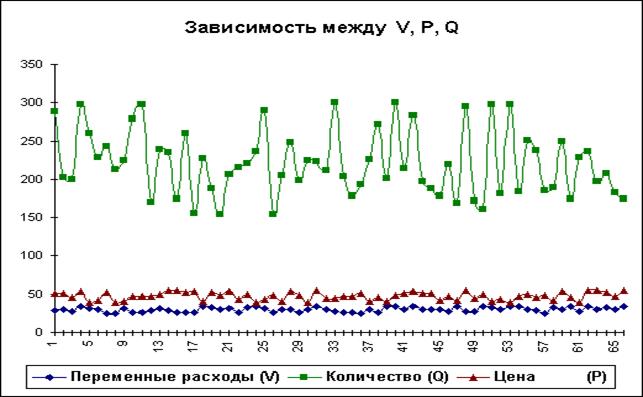
Рис. 1.5  Распределение значений параметров V, P и Q

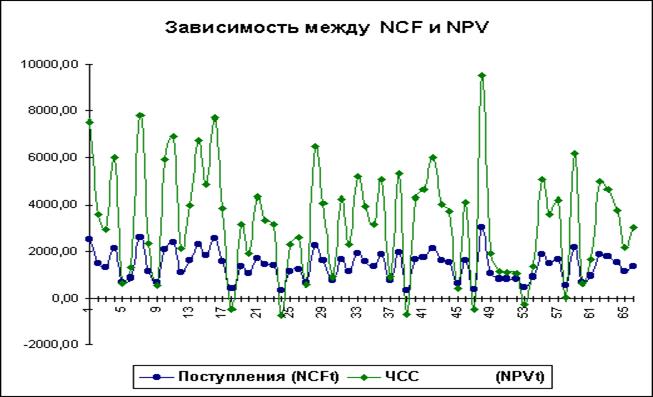
Рис. 1.6 - Зависимость между NCF и NPV

Задание к лабораторной работе № 1

 

1. Постройте модель из теоретической части, проведите с ней эксперименты.

2. Используйте варианты индивидуальных заданий для постановки в построенную модель

3. Постройте отчет по индивидуальному заданию, куда включите фрагмент листа «Имитация» - первые 40 экспериментов, полностью лист «Результаты анализа». Прокомментируйте каждый показатель этого листа с точки зрения оценивания риска инвестиционного проекта.

4. Постройте график зависимости NCF и  NPV для своего задания. Используйте первые 50 значений.

     

Варианты индивидуальных заданий для выполнения лабораторной работы № 1

                                                                                                      

Показатели

Сценарий

Наихудший Наилучший Вероятный

Вариант 1

Объем выпуска - Q 1000 1300 1200 Цена за штуку - P 130 150 140 Переменные затраты - V 145 125 130

Вариант 2

Объем выпуска - Q 1500 3000 2000 Цена за штуку - P 300 450 400 Переменные затраты - V 350 250 300

 

Вариант 3
Объем выпуска – Q	2150	2300	2200
Цена за штуку – P	240	250	245
Переменные затраты – V	250	230	220
Вариант 4
Объем выпуска - Q	800	900	850
Цена за штуку - P	70	85	75
Переменные затраты - V	80	60	50
Вариант 5
Объем выпуска - Q	500	600	550
Цена за штуку - P	45	55	50
Переменные затраты - V	50	40	30

 

 

Лабораторная работа № 2

Лабораторная работа № 3

Ковариация и корреляция

Ковариация выражает степень статистической зависимости между двумя множествами данных и определяется из следующего соотношения:

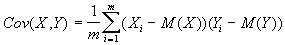
где X, Y - множества значений случайных величин размерности m; M(X) - математическое ожидание случайной величины Х; M(Y) - математическое ожидание случайной величины Y.

Как следует из формулы, положительная ковариация наблюдается в том случае, когда большим значениям случайной величины Х соответствуют большие значения случайной величины Y, т.е. между ними существует тесная прямая взаимосвязь. Соответственно отрицательная ковариация будет иметь место при соответствии малым значениям случайной величины Х больших значений случайной величины Y. При слабо выраженной зависимости значение показателя ковариации близко к 0.

Ковариация зависит от единиц измерения исследуемых величин, что ограничивает ее применение на практике. Более удобным для использования в анализе является производный от нее показатель - коэффициент корреляции R, вычисляемый по формуле:

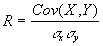
Коэффициент корреляции обладает теми же свойствами, что и ковариация, однако является безразмерной величиной и принимает значения от -1 (характеризует линейную обратную взаимосвязь) до +1 (характеризует линейную прямую взаимосвязь). Для независимых случайных величин значение коэффициента корреляции близко к 0.

Определение количественных характеристик для оценки тесноты взаимосвязи между случайными величинами в ППП EXCEL может быть осуществлено двумя способами:

- с помощью статистических функций КОВАР() и КОРРЕЛ();

- с помощью специальных инструментов статистического анализа.

Если число исследуемых переменных больше 2, более удобным является использование инструментов анализа.

Инструмент анализа данных "Корреляция"

Определим степень тесноты взаимосвязей между переменными V, Q, P, NCF и NPV. При этом в качестве меры будем использовать показатель корреляции R.

1. Выберите "Анализ данных".   Выберите из списка "Инструменты анализа" пункт "Корреляция" и нажмите кнопку "ОК" (рисунок 3.1). Результатом будет появление окна диалога инструмента "Корреляция".

2. Заполните поля диалогового окна, как показано на рисунке 3.2.

Вид полученной ЭТ после выполнения элементарных операций форматирования приведен на рисунке 3.3.

 

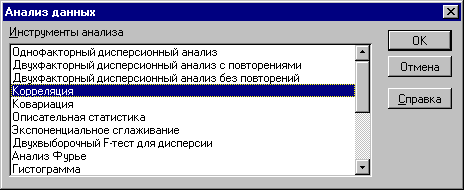
Рис.3.1. Список инструментов анализа (выбор пункта "Корреляция")

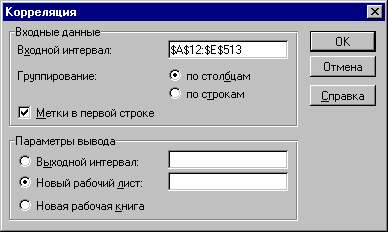
Рис.3.2. Заполнение окна диалога инструмента "Корреляция"

 

 

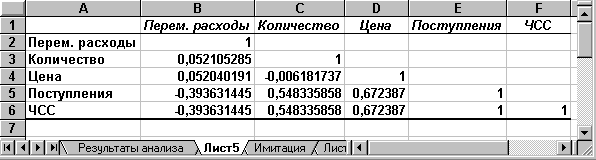
Рис. 3.3. Результаты корреляционного анализа

 

Результаты корреляционного анализа представлены в ЭТ в виде квадратной матрицы, заполненной только наполовину, поскольку значение коэффициента корреляции между двумя случайными величинами не зависит от порядка их обработки. Нетрудно заметить, что эта матрица симметрична относительно главной диагонали, элементы которой равны 1, так как каждая переменная коррелирует сама с собой.

Как следует из результатов корреляционного анализа, выдвинутая в процессе решения предыдущего примера гипотеза о независимости распределений ключевых переменных V, Q, P в целом подтвердилась. Значения коэффициентов корреляции между переменными расходами V, количеством Q и ценой Р (ячейки В3:В4, С4) достаточно близки к 0.

В свою очередь величина показателя NPV напрямую зависит от величины потока платежей (R = 1). Кроме того, существует корреляционная зависимость средней степени между Q и NPV (R = 0,548), P и NPV (R = 0,67). Как и следовало ожидать, между величинами V и NPV существует умеренная обратная корреляционная зависимость (R = -0,39).

Полезность проведения последующего статистического анализа результатов имитационного эксперимента заключается также в том, что во многих случаях он позволяет выявить некорректности в исходных данных, либо даже ошибки в постановке задачи. В частности в рассматриваемом примере, отсутствие взаимосвязи между переменными затратами V и объемами выпуска продукта Q требует дополнительных объяснений, так как с увеличением последнего, величина V также должна расти . Таким образом, установленный диапазон изменений переменных затрат V нуждается в дополнительной проверке и, возможно, корректировке.

Следует отметить, что близкие к нулевым значения коэффициента корреляции R указывают на отсутствие линейной связи между исследуемыми переменными, но не исключают возможности нелинейной зависимости. Кроме того, высокая корреляция не обязательно всегда означает наличие причинной связи, так как две исследуемые переменные могут зависеть от значений третьей.

При проведении имитационного эксперимента и последующего вероятностного анализа полученных результатов мы исходили из предположения о нормальном распределении исходных и выходных показателей. Вместе с тем, справедливость сделанных допущений, по крайней мере для выходного показателя NPV, нуждается в проверке.

Для проверки гипотезы о нормальном распределении случайной величины применяются специальные статистические критерии: Колмогорова-Смирнова, c ². В целом ППП EXCEL позволяет быстро и эффективно осуществить расчет требуемого критерия и провести статистическую оценку гипотез.

     Теоретический материал и инструкции по применению программного средства [3]

Одной из распространенных задач в науке, технике, экономике является аппроксимация численных эмпирических данных аналитическими выражениями. Возможность подобрать параметры уравнения таким образом, чтобы его решение совпало с данными эксперимента, зачастую является доказательством (или опровержением) теории.

Рассмотрим следующую математическую задачу. Известные значения некоторой функции f образуют таблицу 3.1:

Таблица 3.1 Значение фунции
X	x1	x2	. . .	xn
f(x)	y1	y2	. . .	yn

Необходимо построить аналитическую зависимость y = f(x), наиболее близко описывающую результаты эксперимента. Построим функцию y = f(x, a₀, a₁, ..., a_k) таким образом, чтобы сумма квадратов отклонений измеренных значений y_i от расчетных f(x_i ,a₀, a₁, ..., a_k) была наименьшей (см. рис. 3.1).

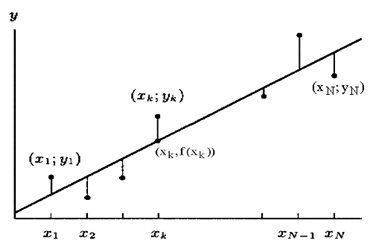
Рис. 3.1 График функции

Математически эта задача равносильна следующей: найти значение параметров a₀, a₁, a₂, ...,a_k, при которых функция принимала бы минимальное значение (формула 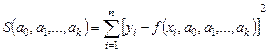3.1).

                                              (3.1)   

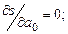
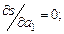
Эта задача сводится к решению системы уравнений 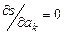(3.2):

                                                            (3.2)

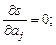
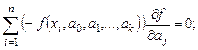
Если параметры a_i входят в зависимость y = f(x,a_o, a₁, …, a_k) линейно, то мы получим систему линейных уравнений 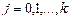(3.3):

                            (3.3)

Решив систему (3.3), найдем параметры a_o, a₁, ..., a_k и получим зависимость y = f(x, a_o, a₁, ..., a_k).

КОРРЕЛ(Массив1;Массив2)

Массив1 - массив значений y.

Массив2 - массив значений y.

Массив1 и Массив2 должны иметь одинаковое количество точек данных.

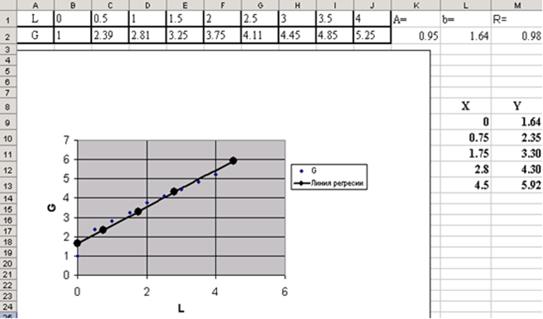
ПРИМЕР 3.1. Известна табличная зависимость G(L). Построить линию регрессии и вычислить ожидаемое значение в точках 0, 0.75, 1.75, 2.8, 4.5.

 

L	0	0,5	1	1,5	2	2,5	3	3,5	4
G	1	2,39	2,81	3,25	3,75	4,11	4,45	4,85	5,25

Введем таблицу значений в лист MS Excel и построим точечный график. Рабочий лист примет вид изображенный на рис. 3.2.

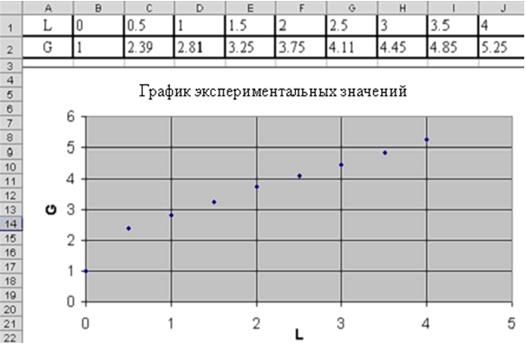
Рис. 3.2 - Точечный график

Для того, чтобы рассчитать значения коэффициентов регрессии а и b выделим ячейки К2:L2, обратимся к мастеру функций и в категории Статистические выберем функцию ЛИНЕЙН. Заполним появившееся диалоговое окно так, как показано на рис. 3.3 и нажмем Ок.

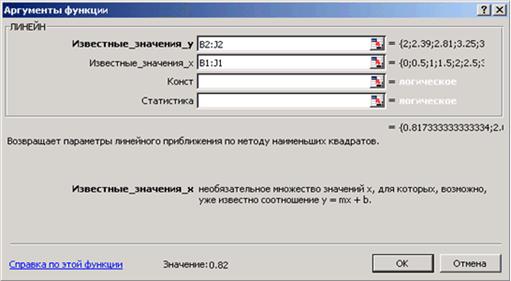
Рис. 3.3 - Форма диалогового окна

В результате вычисленное значение появится только в ячейке К2 (см. рис.3.4). Для того чтобы вычисленное значение появилось и в ячейке L2 необходимо войти в режим редактирования, нажав клавишу F2, а затем нажать комбинацию клавиш CTRL+SHIFT+ENTER.

Для расчета значения коэффициента корреляции в ячейку M2 была введена следующая формула: М2 = КОРРЕЛ(B1:J1;B2:J2) (см. рис. 3.4).

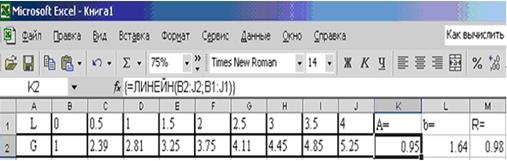
Рис. 3.4 - Пример работы функции ЛИНЕЙН

Для вычисления ожидаемого значения в точках 0, 0.75, 1.75, 2.8, 4.5 занесем их в ячейки L9:L13. Затем выделим диапазон ячеек M10:M13 и введем формулу:

= ТЕНДЕНЦИЯ(B2:J2;B1:J1;L9:L13).

Для того чтобы вычисленные значения появились и в ячейках M10:M13 необходимо нажать комбинацию клавиш CTRL+SHIFT+ENTER.

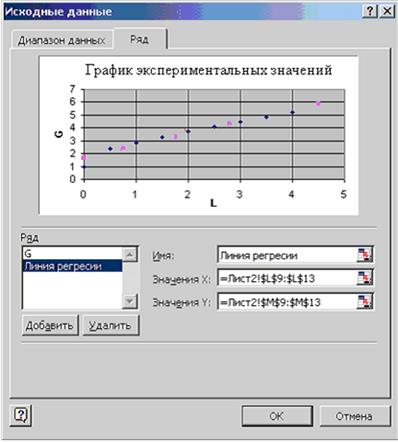
Изобразим линию регрессии на диаграмме. Для этого выделим экспериментальные точки на графике, щелкнем правой кнопкой мыши и выберем команду Исходные данные. В появившемся диалоговом окне (см. рис. 3.5), для добавления линии регрессии щелкнем по кнопке Добавить.

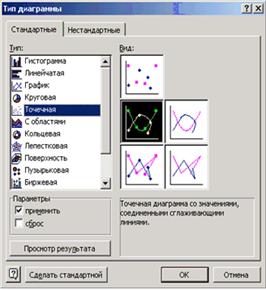
В качестве имени введем Линия регрессии, в качестве Значения Х: L9:L13, в качестве Значения Y: M9:M13. Далее выделяем линию регрессии, для изменения ее типа щелкаем правой кнопкой мыши и выбираем команду Тип диаграммы (см. рис. 3.6). Для форматирования линии регрессии (можно изменить толщину линии, цвет, тип маркера и т.п) дважды щелкаем по ней (см. рис. 3.7).

 

Рис. 3.5 - Форма настройки исходных данных графика функции

Квадратичная функция

Необходимо определить параметры функции y = a_o + a₁x + a₂x².

Составим функцию (3.11):

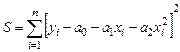                                                                    (3.11)

Для этой функции запишем систему уравнений (3.12):

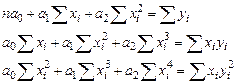                                                                 (3.12)

Для нахождения параметров a_o, a₁, a₂ необходимо решить систему линейных алгебраических уравнений (3.12).

Рис. 3.6 - Окно выбора типа диаграммы	Рис. 3.7 - Окно настройки формата ряда данных

После форматирования графика рабочий лист примет вид, изображенный на рис. 3.8.

Рис. 3.8 - График экспериментальных значений

Кубическая функция

Необходимо определить параметры многочлена третьей степени

y = a_o + a₁ x + a₂ x₂ + a₃ x₃.

Составим функцию S (3.13):

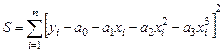                                                         (3.13)

Система уравнений для нахождения параметров a_o, a₁, a₂, a₃ имеет вид (3.14):

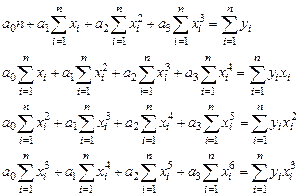                                     (3.14)

Для нахождения параметров a_o, a₁, a₂, a₃ необходимо решить систему четырёх линейных алгебраических уравнений.

Если в качестве аналитической зависимости выберем многочлен k-й степени y = a_o+a₁x+...+a_k x^k, то система уравнений для определения параметров a_i принимает вид (3.15):

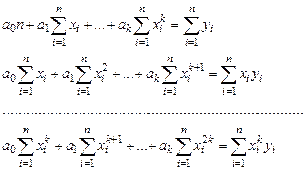                                    (3.15)

Подбор параметров функции y = a x^b

Для нахождения параметров функции y = a x^b проведем логарифмирование функции y: Ln y = Ln a + b Ln x

Сделаем замену Y = ln y; X = ln x. Получим линейную зависимость Y = A + b X. Найдем коэффициенты линии регрессии A и b.определяем a = e^A. Мы получили значение параметров функции y = ax^b.

Подбор параметров функции y = ae^bx

Прологарифмируем выражение y = ae^bx: Ln y = Ln a + bx Ln e ;

Проведём замену Y = Ln y, A = Ln a. Вновь получаем линейную зависимость Y = bx+A. Найдем A и b. Затем определим a = e^A .

Ниже приведены (таблица 3.2) замены переменных, которые преобразовывают функции вида y = f (x, a, b) к линейной зависимости Y = Ax+B.

Таблица 3.2 Замены переменных

Y = f(x,a,b)	Замена

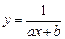
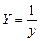
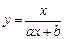
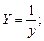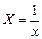
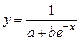
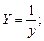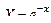
Подбор параметров функции y =a^xb e^cx

Прологарифмируем выражение y = a^xb e^cx, после логарифмирования оно принимает вид (3.16):

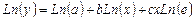                                                                (3.16)

 

Сделаем замену Y=Ln(y), A=Ln(a). После замены выражение (3.16) принимает вид (3.17):

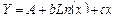                                                                                    (3.17)

Для функции (3.17) составим функцию S см. формулу (3.18):

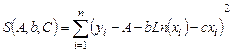                                                                  (3.18)

Параметры A, b и c следует выбрать таким образом, чтобы функция S была минимальной. Необходимым условием минимума S являются соотношения (3.2). Подставим (3.17) в (3.2), и после элементарных преобразований получим систему трёх линейных алгебраических уравнений для определения коэффициентов A, b и c. (система уравнений 3.19)

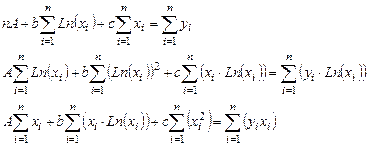                              (3.19)

Решив систему (3.18), получим значения A, b, c. После чего вычисляем a=e^A.

Построение различных аппроксимирующих зависимостей в MS Excel реализовано в виде свойства диаграммы - линия тренда.

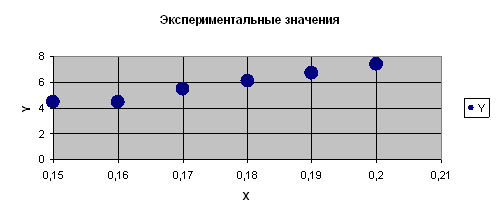
ПРИМЕР 3.2. В результате эксперимента была определена некоторая табличная зависимость. Выбрать и построить аппроксимирующую зависимость. Построить графики табличной и подобранной аналитической зависимости. Вычислить ожидаемое значение в указанных точках (таблица 3.2).

Таблица 3.2. Исходные данные

x1 = 0,1539, x2 = 0,2569, x3 = 0,28
X	0,15	0,16	0,17	0,18	0,19	0,20
Y	4,4817	4,4930	5,4739	6,0496	6,6859	7,3891

Решение задачи можно разбить на следующие этапы:

1. Ввод исходных данных и построение точечного графика (см. рис. 3.9).

2. Добавление к этому графику линии тренда.

Рассмотрим этот процесс подробно.

Рис. 3.9 - Точечный график

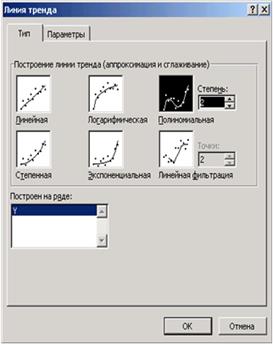
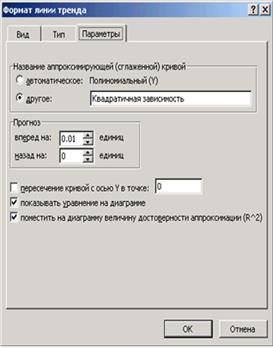
Выделим экспериментальные точки на графике, щелкнем правой кнопкой мыши и воспользуемся командой Добавить линию тренда. Появившееся диалоговое окно (см. рис. 3.10) позволяет построить аппроксимирующую зависимость. На первой вкладке этого окна указывается вид аппроксимирующей зависимости (в нашем случае необходимо выбрать полиномиальную зависимость второй степени). На второй определяются параметры построения:

3. Название аппроксимирующей зависимости.

4. Прогноз вперед (назад) на n единиц (этот параметр определяет, на какое количество единиц вперед (назад) необходимо продлить линию тренда).

5. Показывать ли точку пересечения кривой с прямой Y = const.

6. Показывать аппроксимирующую функцию на диаграмме или нет (параметр показывать уравнение на диаграмме).

7. Помещать ли на диаграмму величину среднеквадратичного отклонения или нет (параметр поместить на диаграмму величину достоверности аппроксимации).

На рис. 3.11 изображена полученная диаграмма.

Рис. 3.10 - Настройка диаграммы

 

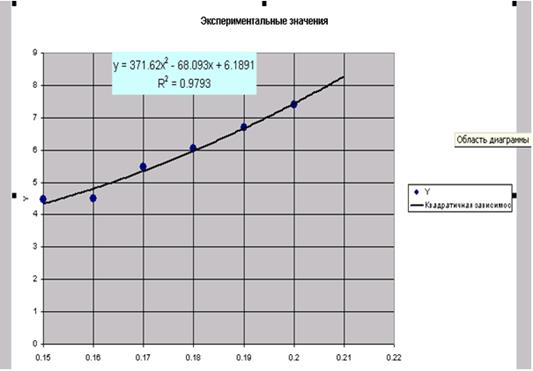
Рис. 3.11 - Результирующий график

Для расчета ожидаемых значений в точках 0.1539, 0.2569, 0.28 введем эти значения в ячейки B4:D4. В ячейку B5 введем формулу подобранной аппроксимирующей зависимости (=371.62*B4^2-68.093*B4+6.1891) и скопируем ее в ячейки C5, D5. Фрагмент рабочего листа примет вид:

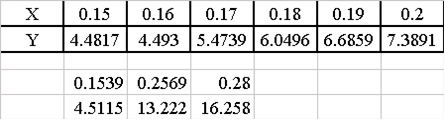
Добавим полученные расчетные значения на диаграмму. Для этого на диаграмме выделим экспериментальные значения, щелкнем правой кнопкой мыши и выберем команду Исходные данные. Добавим туда Рассчитанные значения (см. рис. 3.12).

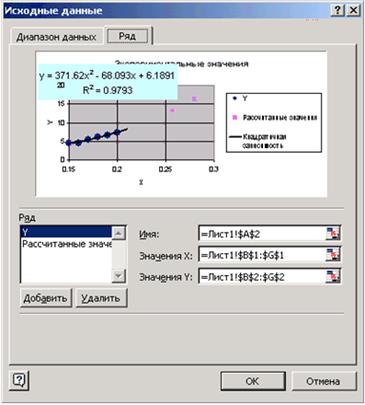
Рис. 3.12 - Добавление ряда в график функции

В результате диаграмма примет вид изображенный на рис. 3.13. Аналогично с помощью линии тренда можно подобрать и параметры других типов зависимостей (линейной, логарифмической и экспоненциальной и т. д.).

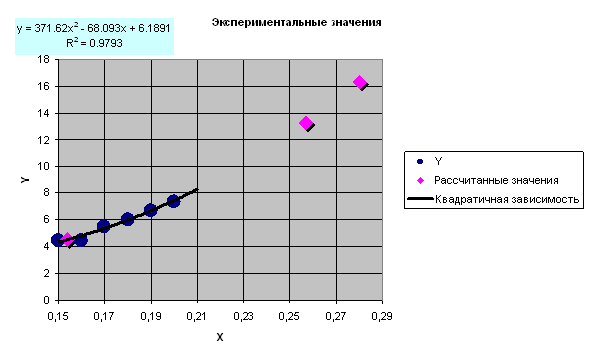
Рис. 3.13 - Результирующий график

ПРИМЕР 3.3. В результате эксперимента получена зависимость z(t) (таблица 3.4):

Таблица 3.4 Экспериментальные данные

T	0,66	0,9	1,17	1,47	1,7	1,74	2,08	2,63	3,12
Z	38,9	68,8	64,4	66,5	64,95	59,36	82,6	90,63	113,5

Подобрать коэффициенты зависимости Z(t)=At⁴+Bt³+Ct²+Dt+K методом наименьших квадратов.

Эта задача эквивалентна задаче нахождения минимума функции пяти переменных (3.20):

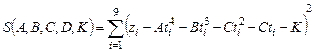                                  (3.20)

Введем табличную зависимость в рабочий лист MS Excel и построим график функции (см. рис.3.15)

Рассмотрим процесс решения задачи оптимизации (8.13). Пусть значения А, В, С, D и К хранятся в ячейках K1:K5. В ячейку B23 введем значение функции At⁴+Bt³+Ct²+Dt+K в первой точке (ячейка B1):

B23 = $K$1*B1^4 + $K$2*B1^3 + $K$3*B1^2 + $K$4*B1 + $K$5.

Получим ожидаемое значение (в начале 0) в точке B1. Затем растянем эту формулу на весь диапазон B23:J23. В ячейку B24 введем формулу, вычисляющую квадрат разности между экспериментальными и расчетными точками:

B24 = (B23-B2)^2,

и растянем ее на диапазон B24:J24. В ячейке В25 будем хранить суммарную квадратичную ошибку (см. формулу 3.20). Для этого введем формулу:

В25 = СУММ(B24:J24).

Теперь осталось с помощью решающего блока (Данные Поиск решения) решить задачу оптимизации без ограничений, заполнив соответствующим образом появившееся диалоговое окно (рис. 3.14).

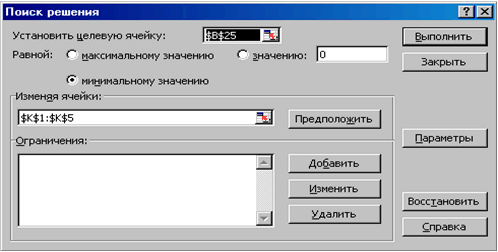
Рис. 3.14 - Окно поиска решения

Результатом работы решающего блока будет вывод в ячейки K1:K5 значений параметров функции At⁴+Bt³+Ct²+Dt+K. В ячейках B23:J23 получим ожидаемые значение функции в исходных точках. Поместим эти точки в виде отдельной линии на графике. В ячейке B25 будет храниться суммарная квадратичная ошибка. Рис. 3.15 отображает внешний вид рабочего листа MS Excel после проведенных вычислений.

Использование решающего блока - это один из эффективных способов реализации метода наименьших квадратов с помощью MS Excel.

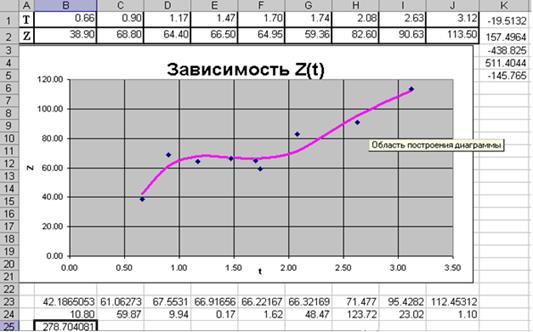
Рис. 3.15 - Графическое представление зависимости

 

 

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Получить у преподавателя варианты выполнения двух заданий.

2. На первом рабочем листе документа MS Excel ввести исходные данные, соответствующие варианту задания. Проанализировать экспериментальную зависимость. Построить график экспериментальных точек.

3. На втором рабочем листе средствами MS Excel рассчитать коэффициенты регрессии, коэффициент корреляции, среднеквадратичные отклонения и суммарную ошибку. Построить в одной графической области экспериментальные точки и линию регрессии.

4. Третий рабочий лист должен содержать вычисление коэффициентов функциональной зависимости, соответствующей варианту задания. Расчет коэффициентов произвести аналитически при помощи метода наименьших квадратов, сведя задачу к задаче оптимизации. Построить в одной графической области экспериментальные точки и график подобранной функциональной зависимости. Определить суммарную ошибку.

5. На четвертом рабочем листе построить линию тренда, если это возможно. Убедится в том, что вычисленные в п.3 коэффициенты совпадают с коэффициентами линии тренда. Провести сравнительный анализ полученных результатов и построить в одной графической области график экспериментальных точек, линию регрессии и график полученной экспериментальной зависимости.

6. Озаглавить рабочие листы согласно тематике вычислений. Исходные данные, результаты вычислений и графики сопровождать соответствующими подписями и пояснениями.

7. Подготовить отчет по выполненной работе и представить его преподавателю.

СОДЕРЖАНИЕ ОТЧЕТА

8. Титульный лист.

9. Тема, цель и основное содержание работы.

10. Описание процесса решения задачи.

11. Промежуточные и итоговые результаты.

12. Выводы по работе.

 

ВАРИАНТЫ ЗАДАНИЙ

Вариант №1. P(s)=As³+Bs²+ С s+D

S	0,00	1,00	1,50	2,00	2,50	3,00	3,50	4,00	4,50	5,00
P	10,00	50,10	39,58	15,40	23,68	33,60	57,78	100,90	149,50	256,00

Вариант № 2. G(s)=Ae^bs

S	0,5	1,5	2	2,5	3	3,5	4	4,5	5
G	3,99	5,65	6,41	7,71	11,215	17,611	27,83	38,19	39,3

Вариант № 3. K(s)=As^b

S	0,5	1	1,5	2	2,5	3	3,5	4
K	1,65	2,1	2	2,1	2,3	2,4	2,22	2,59

Вариант № 4. V(s)=As^b е ^Cs

S	0,2	0,7	1,2	1,7	2,2	2,7	3,2
V	2,3198	2,9569	2,3999	6,4357	6,5781	6,9459	14,6621

Вариант № 5. W(s)=A/(Bs+C)

S	1	2	3	4	5	6	7	8	9
W	0,529	0,298	0,267	0,171	0,156	0,124	0,1	0,078	0,075

Вариант № 6. Q(s)=As²+Bs+C

S	1	1,25	1,5	1,75	2	2,25	2,5	2,75	3
Q	5,21	4,196	3,759	3,672	4,592	4,621	5,758	7,173	9,269

Вариант № 7. Y=x/(Ax-B)

X	3	3,1	3,2	3,3	3,4	3,5	3,6	3,7	3,8	3,9
Y	0,61	0,6	0,592	0,58	0,585	0,583	0,582	0,57	0,572	0,571

Вариант № 8. V=1/(A+Be^-U)

U	2	2,5	3	3,5	4	4,5	5	5,5	6
V	5,197	7,78	11,14	15,09	19,24	23,11	26,25	28,6	30,3

Вариант № 9. R=At^B+14,5

T	1	2	3	4	5	6	7	8	9	10
R	2,11	5,2	5,15	19,27	18,2	30,37	32	31	30,22	31,2

Вариант № 10. R=Ch²+Dh+K

H	2	4	6	8	10	12	14	16
R	0,035	0,09	0,147	0,1	0,24	0,28	0,31	0,34

Вариант №11. G=DL+K

L	0	0,5	1	1,5	2	2,5	3	3,5	4
G	2	2,39	2,81	3,25	3,75	4,11	4,45	4,85	5,25

 

Лабораторная работа № 4

 Оптимизационный анализ в МS Excel

 

В экономике оптимизационные задачи возникают в связи с многочисленностью различных вариантов функционирования экономического объекта, когда возникает ситуация выбора наилучшего варианта по некоторому критерию. Такие задачи называют задачами линейного программирования (ЗЛП). ЗЛП могут быть использованы в следующих случаях:

- оптимальное использование ресурсов;

- планирование производства;

- оптимальное размещение денежных средств;

- планирование штатного расписания.

Математическая модель ЗЛП в общем виде:

Найти min или   max  целевой функции

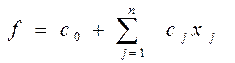
при ограничениях      

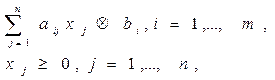
 где  с₀, с _j , a_ij , b_i - действительные числа.

Ограничения могут содержать как знаки равенства, так и неравенства.

Транспортная задача — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение. Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки.

 

Когда суммарный объём предложений (грузов, имеющихся в пунктах отправления) не равен общему объёму спроса на товары (грузы), запрашиваемые пунктами потребления, транспортная задача называется несбалансированной (открытой).

Когда суммарный объем предложения равен объему спроса, транспортная задача закрытого типа или называется закрытой.

Транспортная задача (классическая) — задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределённом количестве) со статичными данными и линеарном подходе (это основные условия задачи).

Для решения таких задач Excel имеет специальный инструмент « Поиск решения». Надстройка «Поиск решения» в Microsoft Excel позволяет напрямую находить оптимальное решение транспортной задачи.

Для добавления надстройки «Поиск решения», если на вкладке «Данные» этого пункта нет перейдите: Файл — Параметры. Слева выберите меню «Надстройки». В основной части выделите «Поиск решения». Затем ниже, нажмите «Перейти». В открывшемся окне отметьте пункт «Поиск решения» и нажмите «Ok». Во вкладке «Данные» появился соответствующий одноименный пункт.

 

Общее условие транспортной задачи:

Найти m*n неотрицательных чисел X_ij– объем перевозок от i-ого поставщика к j-ому потребителю, минимизирующих транспортные затраты по перевозке однородных грузов поставщиков с мощностями (запасами) А_1,А₂…А_м к потребителям с потребностями В₁,В₂…В_n, если известны матрица издержек С_ij – издержки перевозки единицы груза от i-ого поставщика к j-ому потребителю.

 

Математическая постановка задачи:

 

Целевая функция

 

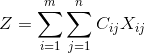
Ограничения

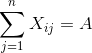для i=1,2….m

 

При этом необходимо, чтобы транспортная задача была закрытой - суммарная мощность поставщиков должна быть равна суммарной потребности потребителей.

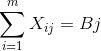для j=1,2….n

 

Если задача открытого типа, для балансирования суммарных запасов и потребностей вводится или фиктивный поставщик, запасы которого равны превышению суммарных потребностей над суммарными запасами, или фиктивный потребитель, потребности которого равны превышению суммарных запасов над суммарными потребностями. При этом матрица издержек дополняется строкой или столбцом с нулевыми элементами.

 

Примеры решения оптимизационных задач в MS EXCEL

 

    Постановка задачи о планировании производства

    Небольшая фабрика выпускает 2 вида товаров. Для производства товаров используется два исходных продукта А и В. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 тонн соответственно. Данные по производству товаров приведены в таблице 4.1.

Таблица 4.1 - Исходные данные задачи

Исходный продукт	расход исходного продукта на 1 тонну товара		Максимально возможный запас
	товар 1	товар 2
А	1	2	6
В	2	1	8

        

Изучение рынка сбыта показало, что суточный спрос на товар 1 никогда не превышает спрос на товар 2 на 1 тонну. Установлено, что спрос на товар 1 никогда не превышает 2 тонны в сутки. Цена товара 1 – 3000 руб, товара 2 – 2000 рублей.

    Какое количество товаров должна производить фабрика, чтобы максимизировать свою прибыль. 

 

    Математическая постановка задачи:

    Переменные:

    Х1 – количество товара 1, Х2 – количество товара 2 (в тоннах).

Целевая функция:

f(x) = 3000*X1 + 2000*X2 ® max

Ограничения:

Х1 + 2*Х2 £ 6;

2*Х1 + Х2 £ 8;

Х1, Х2 ³ 0;

Х1 – Х2 £ 1;

Х1£ 2.

 

    Технология решения задачи

1. Разработайте шаблон для решения задачи. Для этого в ячейку А1 запишите “Переменные”; в ячейку А2 -“Х1”, в В2 – “Х2”; в А4 – “Функция цели”; в С4 – формулу “=3000*А3 + 2000*В3”; в А6 – “Ограничения”; в А7 – “=А3 + 2*В3”; А8 – “=2*А3 + В3”; А9 – “=В3-А3”; А10 – “=В3”; в В7 – “6”; в В8 – “8”; в В9 – “1”; в В10 – “2”.

2. Установите надстройку «Поиск решения» - Главная кнопка – Параметры - Надстройки – Поиск решения – Перейти - ОК. Выполните команду ДАННЫЕ – ПОИСК РЕШЕНИЯ, На экране отобразится диалоговое окно Поиск решения (рис.4.1). Заполните его в соответствии с приведенным рисунком.

 

 

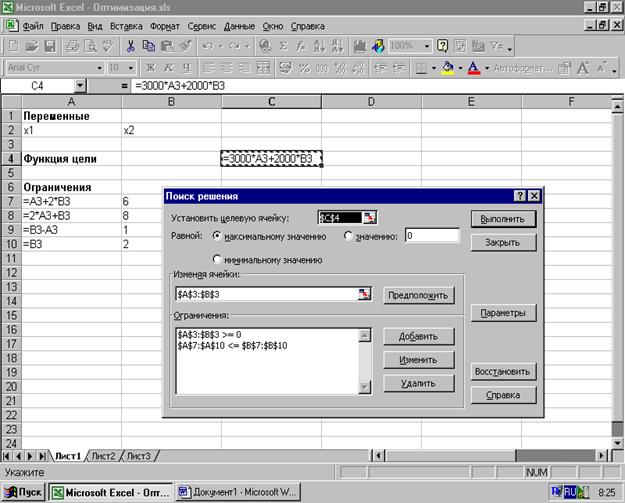
    Рис. 4.1. Решение задачи с помощью средства Поиск решения.

 

3. Нажмите кнопку Параметры. На экране отобразится диалоговое окно Параметры поиска решения. В диалоговом окне можно изменять условия и варианты поиска решения исследуемой задачи, а также загружать и сохранять оптимизируемые модели. В нашей задаче оставим все параметры, установленные по умолчанию, предварительно установив флажок Линейная модель.

4. Нажмите кнопку Выполнить. На экране отобразится окно Результаты поиска решения.

Поиск решения нашел оптимальный план производства товаров, дающий максимальную прибыль. Оптимальным является производство в сутки 3 1/3 товара 1 и 1 1/3 товара 2. Этот объем производства принесет 12 1/3 тыс. руб. прибыли.

 

Транспортная задача

 

Дано 5 производителей А_1, А₂, А_3, А₄, А₅, мощность (запасы) которых соответственно равна(равны): 20, 45, 25, 30,20. И четыре потребителя В₁, В₂, В₃, В₄, потребность которых в продукте составляет соответственно: 45, 50, 20, 25.

Также известна матрица издержек С_ij – издержки перевозки единицы груза от i-ого поставщика к j-ому потребителю.

Ее можно представить таблицей:

 

12	9	10	4
4	7	7	6
7	11	5	8
9	6	9	9
10	11	6	5

 

Полностью, условие транспортной задачи, можно представить таблицей следующего содержания:

 

	45	50	20	25
20	12	9	10	4
45	4	7	7	6
25	7	11	5	8
30	9	6	9	9
20	10	11	6	5

 

 

Решение:

 

Введите исходные данные, начиная с ячейки А1

 

В ячейку Н1 введите формулу: СУММПРОИЗВ(В2:E6;B9:E13)

 

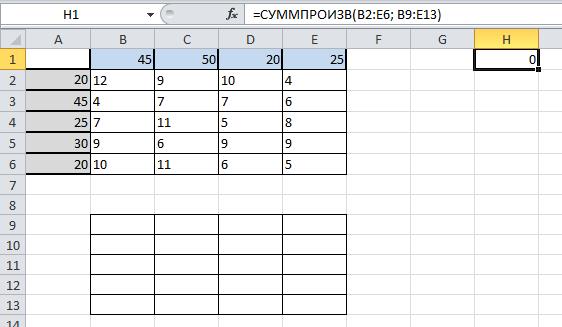
В ячейку A9 введите формулу СУММ(B9:Е9) и растяните её до А13

 

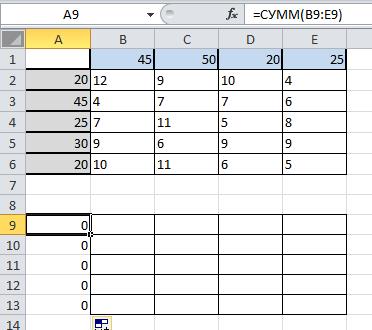
В ячейку B8 введите формулу СУММ(B9:B13) и скопируйте ее в диапазон от B8 до E8:

 

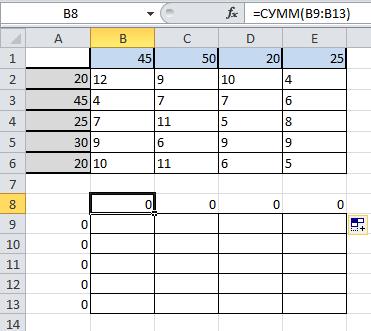
Для решения задачи на панели вкладок выберите вкладку «Данные», а затем «Поиск решения»:

 

Заполните открывшееся окно в соответствие с рисунком и нажмите Найти решение:

 

 

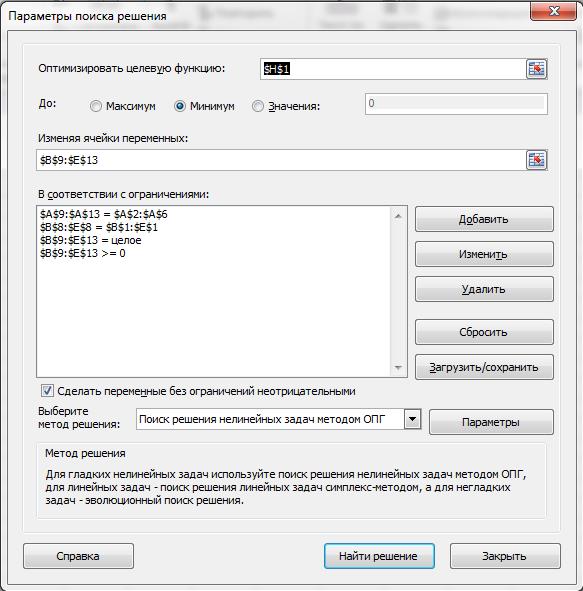
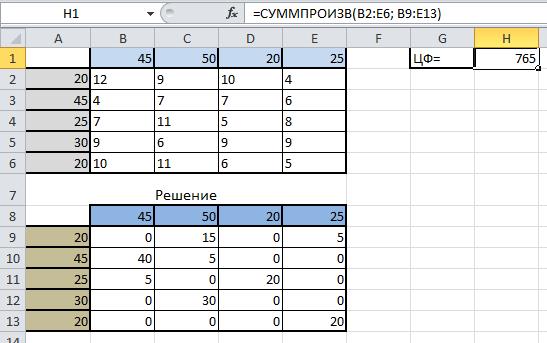
В диапазоне B9:E13 Вы получите результат решения транспортной задачи (т.е. значение в ячейке соответствует количеству груза перевезенного от i-ого поставщика к j-ому потребителю).

В диапазоне A9:A13 количество груза, которое необходимо вывезти от поставщиков.

В диапазоне B8:E8 количество которое будет доставлено потребителям согласно найденному решению.

В ячейке H1 значение целевой функции при найденном решении (минимально возможное - 765). Это значение получено в результате умножения стоимости перевозки от от i-ого поставщика к j-ому потребителю на количество единиц груза, которые необходимо перевезти между ними.

 

Оформим полученный результат и получим следующее:

 

 

Задания для самостоятельного выполнения.

1.Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуются 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй моделей равна $30 и $20 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.

2. Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках (таблица 4.3). Время использования этих станков для производства данных изделий ограничено 10 ч в сутки. Найти оптимальный объем производства изделий каждого вида.

Таблица 4.3 – Исходные данные по задаче

Изделие	Время обработки одного изделия, мин				Удельная прибыль, $
	Станок 1		Станок 2	Станок 3
1		10	6	8	2
2		5	20	15	3

  

3. Фирма производит два вида продукции – А и В. Объем сбыта продукции вида А составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 кг. Расход сырья на единицу продукции А составляет 2 кг, а на единицу продукции В – 4 кг. Цены продукции А и В равны $20 и $40 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.

4. Фирма выпускает ковбойские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $8, а фасона 2 – $5. Определить, какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.

5. Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков приведено в таблице 4.4.

 

Таблица 4.4 – Исходные данные для задачи

Станок

Лабораторная работа № 5

Лабораторная работа № 6

Зачетное задание

1. В соответствии с заданием варианта выбрать из исходных данных (таблицы 5.1 - 5.3)   значения соответствующих показателей за 7 периодов. Перенести в Excel.

2. Сформировать на новом листе Excel   таблицу на основе выбранных данных (путем копирования и вставки транспонированием) так, чтобы значения показателей из строк преобразовались в столбцы.

3. Установить пакет анализа (сервис – надстройки – пакет анализа – установить) и режим ручных вычислений (сервис – параметры – вычисления вручную – установить)

4. Используя Сервис-Анализ данных – корреляция построить корреляционную таблицу, характеризующую взаимосвязи между четырьмя показателями.  

5. Используя Сервис – Анализ данных – Описательная статистика построить таблицу описательной статистики

8. Используя Сервис – Анализ данных – Генерация случайных чисел получить еще по двадцать значений каждого показателя. Снова построить корреляционную таблицу, сравнить с предыдущей.

6. Провести прогноз еще 10 значений каждого показателя. Построить диаграммы с линией тренда.

6. Подготовить отчет, в котором отразить все созданные таблицы, прокомментировать результаты статистических исследований выбранных данных.

Варианты заданий:

Даны документы финансовой отчетности некоторой организации за 7 месяцев. Необходимо исследовать соответствующие показатели.

1. Исходные данные для исследования: внеоборотные активы, долгосрочные финансовые вложения, запасы, краткосрочные финансовые вложения (таблица 5.1)

2. Исходные данные для исследования: основные средства, долгосрочные финансовые вложения, оборотные активы, незавершенное производство (таблица 5.1)

3. Исходные данные для исследования: внеоборотные активы, запасы, долгосрочные дебиторы, денежные средства (таблица 5.1)

4. Исходные данные для исследования: основные средства, долгосрочные финансовые вложения, краткосрочные финансовые вложения, денежные средства (таблица 5.1)

5. Исходные данные для исследования: собственный капитал, добавочный капитал, краткосрочные кредиты и займы, краткосрочная кредиторская задолженность перед поставщиками и подрядчиками (таблица 5.2)

6. Исходные данные для исследования: прибыль, краткосрочные обязательства, задолженность участникам (учредителям), собственный капитал (таблица 5.2)

7. Исходные данные для исследования:  оборотные активы (таблица 5.1), прибыль , краткосрочные кредиты и займы, краткосрочная задолженность перед поставщиками и подрядчиками (таблица 5.2)

8. Исходные данные для исследования: чистая выручка, полная себестоимость, валовая прибыль, чистая прибыль (таблица 5.3)

9. Исходные данные для исследования: оборотные активы (таблица 5.1), собственный капитал (таблица 5.2), себестоимость, валовая прибыль (таблица 5.3)

10.  Исходные данные для исследования: денежные средства (таблица 5.1), краткосрочные обязательства (таблица 5.2), себестоимость, чистая прибыль (таблица 5.3)

 

Таблица 5.1 - Активы аналитического баланса

Наименование показателя	01.04.	01.05.	01.06.	01.07.	01.08.	01.09.	01.10.
I. ВНЕОБОРОТНЫЕ АКТИВЫ	11948	7540	7486	21948	7487	7391	11898
Нематериальные активы	91	93	94	91	95	96	91
Основные средства	700	560	505	700	505	408	650

Продолжение таблицы 5.1

Вложения во внеоборотные активы
Долгосрочные финансовые вложения	11157	6887	6887	13157	6887	6887	11157
Прочие внеоборотные активы				8000
II. ОБОРОТНЫЕ АКТИВЫ	39455	54548	43204	39455	43438	41143	38855
Запасы	11615	17219	16255	11615	15800	15068	11615
в том числе
сырье и материалы	2200	7811	10790	2200	5633	5651	2200
незавершенное производство	9415	9408	5465	9415	10167	9417	9415
готовая продукция
товары отгруженные
расходы будущих периодов
НДС по приобретенным ценностям	5700	5998	5547	5700	5547	5147	5700
Долгосрочные дебиторы	5186	14005	3313	5186	3744	3744	5186
в том числе
покупатели и заказчики	4186	14005	3313	4186	3744	3744	4186
Краткосрочные дебиторы	5483	7921	9123	5483	10168	9559	5483
в том числе
покупатели и заказчики	3861	6399	7601	3861	8646	7037	3861
Краткосрочные финансовые вложения	4572	4572	4572	4572	4572	4572	4571
Денежные средства	6899	4831	4394	6899	3606	3053	6300

 

Таблица 5.2 – Пассивы аналитического баланса

Наименование показателя	01.04.	01.05.	01.06.	01.05.	01.06.	01.07.	01.08.
I. СОБСТВЕННЫЙ КАПИТАЛ (фактический)	17509	22122	8378	17509	5879	6349	17509
Уставный капитал (фактический)	532	532	532	532	532	532	532
Собственные акции, выкупленные у акционеров	14	14	14	14	14	14	14
Добавочный капитал	1982	1982	1982	1982	1982	982	1982
Целевое финансирование	2354			2354			2354
Прибыль, резервы (фактические)	12655	19622	5878	12655	3379	4849	12655
II. ДОЛГОСРОЧНЫЕ ОБЯЗАТЕЛЬСТВА					1360	1560
III. КРАТКОСРОЧНЫЕ ОБЯЗАТЕЛЬСТВА	33894	39966	42312	43894	43686	40625	33244
Краткосрочные кредиты и займы	4800	6255	8255	6800	6200	7130	5200
Краткосрочная кредиторская задолж.	28652	33271	33617	36652	37046	33054	27603
в том числе
перед поставщиками и подрядчиками	17484	24979	27143	25484	30166	25384	17484
перед персоналом организации	472	637	472	472	482	709	472
перед гос. внебюджетными фондами	1637	1546	1346	1637	1546	1546	1637
перед бюджетом	2505	1641	1568	2505	1714	2347	2505
по авансам полученным	2900	1800	420	2900	70		2900
перед прочими кредиторами	3654	2668	2668	3654	3068	3068	2605
Задолженность участникам (учредителям)	440	440	440	440	440	440	440

Таблица 5.3 – Отчет о прибылях и убытках

Наименование показателя	01.04.	01.05.	01.06.	01.07.	01.08.	01.09.	01.10.
I.ОСНОВНАЯ ДЕЯТЕЛЬНОСТЬ
Чистая выручка	3881	4680	5196	6457	2281	2962	3443
Себестоимость	1140	1500	6377	7586	2742	1963	2352
Валовая прибыль	2741	3180	-1181	-1129	-461	999	1091
Полная себестоимость	1140	1500	6377	7586	2742	1963	2352
в том числе:
коммерческие расходы
управленческие расходы
Результат от основной деятельности	2741	3180	-1181	-1129	-461	999	1091
II.ПРОЧАЯ ДЕЯТЕЛЬНОСТЬ
Прочие доходы	1100	100	800	1000	1000	605	893
Прочие расходы	716	94	3458	465	1093	663	595
Результат от прочей деятельности	384	6	-2658	535	-93	-58	298
Прибыль (убыток) до налогообложения	3125	3186	-3839	-594	-554	941	1389
Налог на прибыль и обязательные платежи	456	307	286	1468		103	172
Чистая прибыль (убыток)	2669	2879	-4125	-2062	-554	838	1217

 

 

Список литературы

 

1. Гарнаев А.Ю. Excel, VBA, Internet в экономике и финансах. – СПб.: БХВ-Петербург, 2003. – 816 с.

2. Емельянов А.А. Имитационное моделирование в управлении рисками – СПб: СПбГИЭА, 2000. – 376 с.

3. Петров С В. Методы научных исследований. Методические указания по выполнению лабораторных работ. Калининград: изд-во КГТУ, 2013 – 93 с.

4. Г.Г. Арунянц. Моделирование экономических процессов. Практикум – Калининград: БИЭФ, 2009. – 223 с.

 

Статистическая обработка данных и имитационное моделирование в среде табличного процессора Excel

 

 

 

 

Методические указания к лабораторным работам

для магистров экономического факультета специальности

080200 – Менеджмент

 

Калининград, 2012

 

 

 

Оглавление

Введение. 3

Лабораторная работа № 1. 4

Моделирование риска инвестиционного проекта с использованием.. 4

встроенных функций ППП MS Excel 2007. 4

Лабораторная работа № 2. 19

Моделирование риска инвестиционного проекта с использованием.. 19

инструмента «Генератор случайных чисел» MS Excel 19

Лабораторная работа № 3. 31

Статистический анализ результатов имитационного эксперимента. 31

Лабораторная работа № 4. 41

Оптимизационный анализ в МS Excel 41

Лабораторная работа № 5. 48

Прогнозирование данных в MS Excel 48

Лабораторная работа № 6. 52

Зачетное задание. 52

Список литературы.. 56

 

 

Введение

 

Данное пособие с лабораторным практикумом предназначено для студентов специальности 0802000 – «Менеджмент », изучающих дисциплину «Информационные технологии в менеджменте». Выбор программного продукта MS Excel 2007 обусловлен двумя причинами. Во-первых, данная программа является наиболее мощным и гибким средством обработки больших объемов цифровых данных со встроенными механизмами финансового и статистического анализа. Полученные в ходе выполнения лабораторных работ навыки будут в дальнейшем использованы магистрантами при подготовке выпускных магистерских диссертаций. Во-вторых, данный программный продукт очень широко распространен и доступен, поэтому каждый студент может успешно использовать его в дальнейшей профессиональной деятельности.

Пособие состоит из пяти лабораторных работ. В начале каждой работы приводятся краткие теоретические сведения, необходимые для выполнения работы. Далее описывается технология выполнения работы. Также для каждой работы предусмотрено конкретное задание по вариантам. Предложения, помеченные цифрами в тексте пособия, студент должен выполнять. Рассматриваемый перечень лабораторных работ может быть выполнен в течение одного семестра.

Лабораторные работы выполняются в компьютерных классах университета. Студентам рекомендуется иметь устройство для сохранения выполненных работ, т. к. задания в некоторых лабораторных работах предполагают использование результатов предыдущих работ.

При подготовке лабораторного практикума использованы некоторые примеры из литературы приведённого списка.  

 

 

 

Лабораторная работа № 1