Вычисление коэффициентов регрессии осуществляется с помощью функции ЛИНЕЙН():
ЛИНЕЙН(Значения_y; Значения_x; Конст; статистика)
Значения_y - массив значений y.
Значения_x- необязательный массив значений x, если массив х опущен, то предполагается, что это массив {1;2;3;...} такого же размера, как и Значения_y.
Конст - логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если Конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом. Если аргумент Конст имеет значение ЛОЖЬ, то b полагается равным 0 и значения a подбираются так, чтобы выполнялось соотношение y = ax.
Статистика - логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. Если аргумент статистика имеет значение ИСТИНА, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику. Если аргумент статистика имеет значение ЛОЖЬ или опущен, то функция ЛИНЕЙН возвращает только коэффициент a и постоянную b.
Для вычисления множества точек на линии регрессии используется функция ТЕНДЕНЦИЯ.
ТЕНДЕНЦИЯ(Значения_y; Значения_x; Новые_значения_x; Конст)
Значения_y- массив значений y, которые уже известны для соотношения y = ax + b.
Значения_x- массив значений x.
Новые_значения_x- новый массив значений, для которых ТЕНДЕНЦИЯ возвращает соответствующие значения y. Если Новые_значения_x опущены, то предполагается, что они совпадают с массивом значений х.
Конст - логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если Конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом. Если Конст имеет значение ЛОЖЬ, то b полагается равным 0, и значения а подбираются таким образом, чтобы выполнялось соотношение y = ax. Необходимо помнить, что результатом функций ЛИНЕЙН, ТЕНДЕНЦИЯ является множество значений - массив.
Для расчета коэффициента корреляции используется функция КОРРЕЛ, возвращающая значения коэффициента корреляции:
КОРРЕЛ(Массив1;Массив2)
Массив1 - массив значений y.
Массив2 - массив значений y.
Массив1 и Массив2 должны иметь одинаковое количество точек данных.
ПРИМЕР 3.1. Известна табличная зависимость G(L). Построить линию регрессии и вычислить ожидаемое значение в точках 0, 0.75, 1.75, 2.8, 4.5.
| L | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 |
| G | 1 | 2,39 | 2,81 | 3,25 | 3,75 | 4,11 | 4,45 | 4,85 | 5,25 |
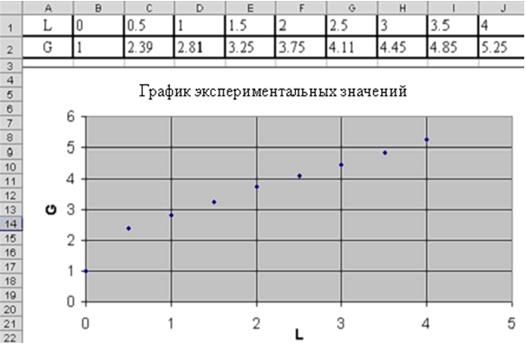
Введем таблицу значений в лист MS Excel и построим точечный график. Рабочий лист примет вид изображенный на рис. 3.2.
|
| Рис. 3.2 - Точечный график |
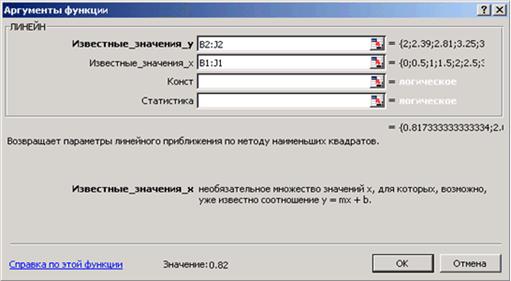
Для того, чтобы рассчитать значения коэффициентов регрессии а и b выделим ячейки К2:L2, обратимся к мастеру функций и в категории Статистические выберем функцию ЛИНЕЙН. Заполним появившееся диалоговое окно так, как показано на рис. 3.3 и нажмем Ок.
|
| Рис. 3.3 - Форма диалогового окна |
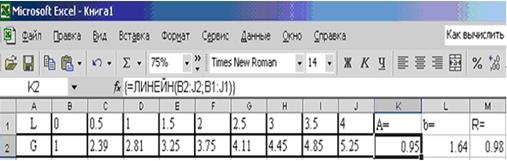
В результате вычисленное значение появится только в ячейке К2 (см. рис.3.4). Для того чтобы вычисленное значение появилось и в ячейке L2 необходимо войти в режим редактирования, нажав клавишу F2, а затем нажать комбинацию клавиш CTRL+SHIFT+ENTER.
Для расчета значения коэффициента корреляции в ячейку M2 была введена следующая формула: М2 = КОРРЕЛ(B1:J1;B2:J2) (см. рис. 3.4).
|
| Рис. 3.4 - Пример работы функции ЛИНЕЙН |
Для вычисления ожидаемого значения в точках 0, 0.75, 1.75, 2.8, 4.5 занесем их в ячейки L9:L13. Затем выделим диапазон ячеек M10:M13 и введем формулу:
= ТЕНДЕНЦИЯ(B2:J2;B1:J1;L9:L13).
Для того чтобы вычисленные значения появились и в ячейках M10:M13 необходимо нажать комбинацию клавиш CTRL+SHIFT+ENTER.
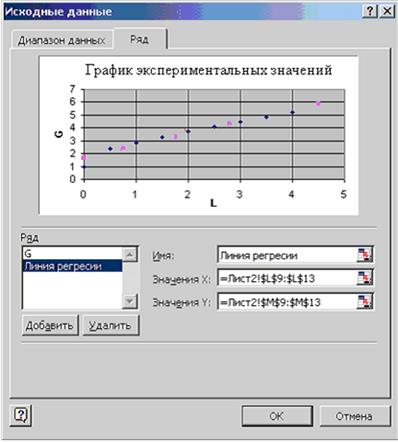
Изобразим линию регрессии на диаграмме. Для этого выделим экспериментальные точки на графике, щелкнем правой кнопкой мыши и выберем команду Исходные данные. В появившемся диалоговом окне (см. рис. 3.5), для добавления линии регрессии щелкнем по кнопке Добавить.
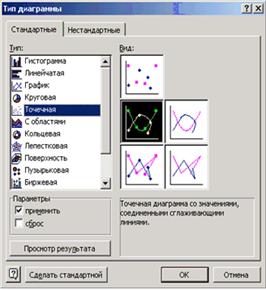
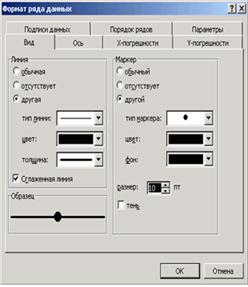
В качестве имени введем Линия регрессии, в качестве Значения Х: L9:L13, в качестве Значения Y: M9:M13. Далее выделяем линию регрессии, для изменения ее типа щелкаем правой кнопкой мыши и выбираем команду Тип диаграммы (см. рис. 3.6). Для форматирования линии регрессии (можно изменить толщину линии, цвет, тип маркера и т.п) дважды щелкаем по ней (см. рис. 3.7).
|
| Рис. 3.5 - Форма настройки исходных данных графика функции |
Квадратичная функция
Необходимо определить параметры функции y = ao + a1x + a2x2.
Составим функцию (3.11):
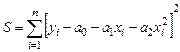(3.11)
Для этой функции запишем систему уравнений (3.12):
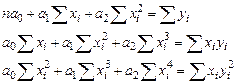(3.12)
Для нахождения параметров ao, a1, a2 необходимо решить систему линейных алгебраических уравнений (3.12).
| 
|
| Рис. 3.6 - Окно выбора типа диаграммы | Рис. 3.7 - Окно настройки формата ряда данных |
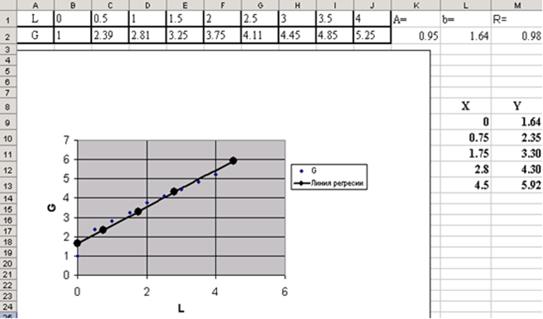
После форматирования графика рабочий лист примет вид, изображенный на рис. 3.8.
|
| Рис. 3.8 - График экспериментальных значений |
Кубическая функция
Необходимо определить параметры многочлена третьей степени
y = ao + a1 x + a2 x2 + a3 x3.
Составим функцию S (3.13):
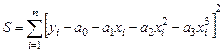(3.13)
Система уравнений для нахождения параметров ao, a1, a2, a3 имеет вид (3.14):
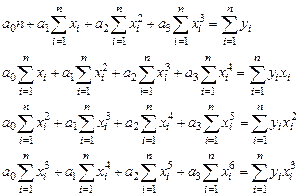(3.14)
Для нахождения параметров ao, a1, a2, a3 необходимо решить систему четырёх линейных алгебраических уравнений.
Если в качестве аналитической зависимости выберем многочлен k-й степени y = ao+a1x+...+ak xk, то система уравнений для определения параметров ai принимает вид (3.15):
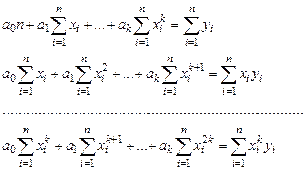(3.15)
Подбор параметров функции y = a xb
Для нахождения параметров функции y = a xb проведем логарифмирование функции y: Ln y = Ln a + b Ln x
Сделаем замену Y = ln y; X = ln x. Получим линейную зависимость Y = A + b X. Найдем коэффициенты линии регрессии A и b.определяем a = eA. Мы получили значение параметров функции y = axb.
Подбор параметров функции y = aebx
Прологарифмируем выражение y = aebx: Ln y = Ln a + bx Ln e ;
Проведём замену Y = Ln y, A = Ln a. Вновь получаем линейную зависимость Y = bx+A. Найдем A и b. Затем определим a = eA .
Ниже приведены (таблица 3.2) замены переменных, которые преобразовывают функции вида y = f (x, a, b) к линейной зависимости Y = Ax+B.
Таблица 3.2 Замены переменных
| Y = f(x,a,b) | Замена |
| 
|
|  
|
| 
|
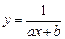
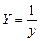
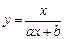
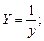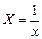
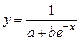
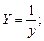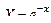
Подбор параметров функции y =axb ecx
Прологарифмируем выражение y = axb ecx, после логарифмирования оно принимает вид (3.16):
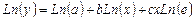(3.16)
Сделаем замену Y=Ln(y), A=Ln(a). После замены выражение (3.16) принимает вид (3.17):
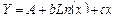(3.17)
Для функции (3.17) составим функцию S см. формулу (3.18):
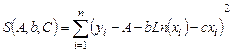(3.18)
Параметры A, b и c следует выбрать таким образом, чтобы функция S была минимальной. Необходимым условием минимума S являются соотношения (3.2). Подставим (3.17) в (3.2), и после элементарных преобразований получим систему трёх линейных алгебраических уравнений для определения коэффициентов A, b и c. (система уравнений 3.19)
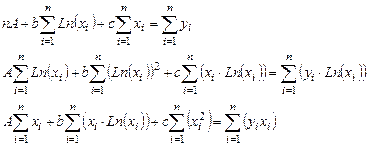(3.19)
Решив систему (3.18), получим значения A, b, c. После чего вычисляем a=eA.
Построение различных аппроксимирующих зависимостей в MS Excel реализовано в виде свойства диаграммы - линия тренда.
ПРИМЕР 3.2. В результате эксперимента была определена некоторая табличная зависимость. Выбрать и построить аппроксимирующую зависимость. Построить графики табличной и подобранной аналитической зависимости. Вычислить ожидаемое значение в указанных точках (таблица 3.2).
Таблица 3.2. Исходные данные
| x1 = 0,1539, x2 = 0,2569, x3 = 0,28 | ||||||
| X | 0,15 | 0,16 | 0,17 | 0,18 | 0,19 | 0,20 |
| Y | 4,4817 | 4,4930 | 5,4739 | 6,0496 | 6,6859 | 7,3891 |
Решение задачи можно разбить на следующие этапы:
1. Ввод исходных данных и построение точечного графика (см. рис. 3.9).
2. Добавление к этому графику линии тренда.
Рассмотрим этот процесс подробно.
|
| Рис. 3.9 - Точечный график |
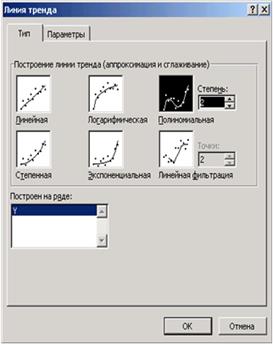
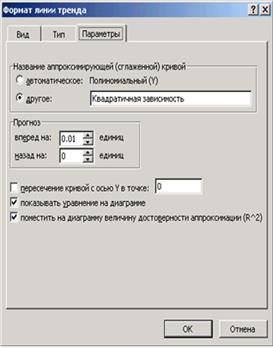
Выделим экспериментальные точки на графике, щелкнем правой кнопкой мыши и воспользуемся командой Добавить линию тренда. Появившееся диалоговое окно (см. рис. 3.10) позволяет построить аппроксимирующую зависимость. На первой вкладке этого окна указывается вид аппроксимирующей зависимости (в нашем случае необходимо выбрать полиномиальную зависимость второй степени). На второй определяются параметры построения:
3. Название аппроксимирующей зависимости.
4. Прогноз вперед (назад) на n единиц (этот параметр определяет, на какое количество единиц вперед (назад) необходимо продлить линию тренда).
5. Показывать ли точку пересечения кривой с прямой Y = const.
6. Показывать аппроксимирующую функцию на диаграмме или нет (параметр показывать уравнение на диаграмме).
7. Помещать ли на диаграмму величину среднеквадратичного отклонения или нет (параметр поместить на диаграмму величину достоверности аппроксимации).
На рис. 3.11 изображена полученная диаграмма.
| 
|
| Рис. 3.10 - Настройка диаграммы | |
|
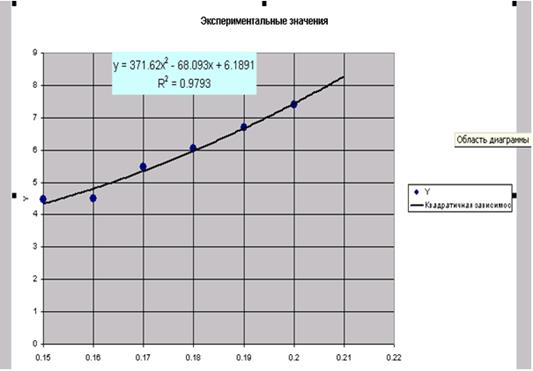
| Рис. 3.11 - Результирующий график |
Для расчета ожидаемых значений в точках 0.1539, 0.2569, 0.28 введем эти значения в ячейки B4:D4. В ячейку B5 введем формулу подобранной аппроксимирующей зависимости (=371.62*B4^2-68.093*B4+6.1891) и скопируем ее в ячейки C5, D5. Фрагмент рабочего листа примет вид:
|
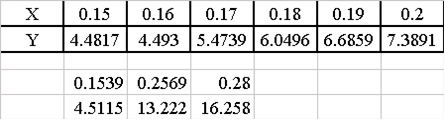
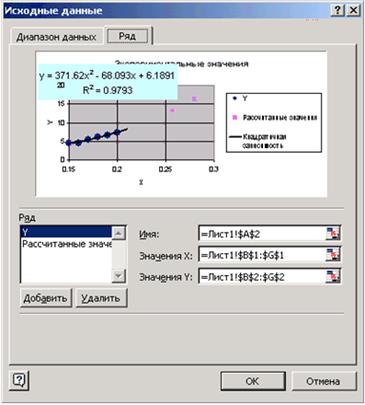
Добавим полученные расчетные значения на диаграмму. Для этого на диаграмме выделим экспериментальные значения, щелкнем правой кнопкой мыши и выберем команду Исходные данные. Добавим туда Рассчитанные значения (см. рис. 3.12).
|
| Рис. 3.12 - Добавление ряда в график функции |
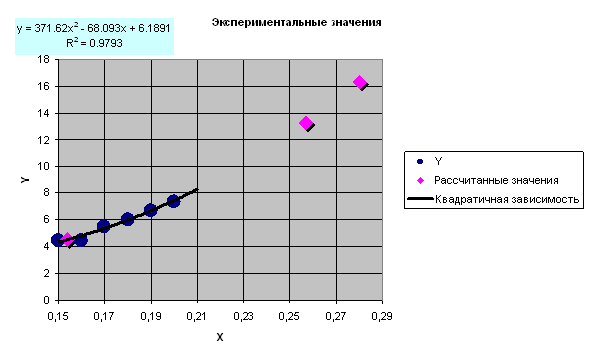
В результате диаграмма примет вид изображенный на рис. 3.13. Аналогично с помощью линии тренда можно подобрать и параметры других типов зависимостей (линейной, логарифмической и экспоненциальной и т. д.).
|
| Рис. 3.13 - Результирующий график |
ПРИМЕР 3.3. В результате эксперимента получена зависимость z(t) (таблица 3.4):
Таблица 3.4 Экспериментальные данные
| T | 0,66 | 0,9 | 1,17 | 1,47 | 1,7 | 1,74 | 2,08 | 2,63 | 3,12 |
| Z | 38,9 | 68,8 | 64,4 | 66,5 | 64,95 | 59,36 | 82,6 | 90,63 | 113,5 |
Подобрать коэффициенты зависимости Z(t)=At4+Bt3+Ct2+Dt+K методом наименьших квадратов.
Эта задача эквивалентна задаче нахождения минимума функции пяти переменных (3.20):
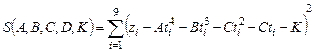(3.20)
Введем табличную зависимость в рабочий лист MS Excel и построим график функции (см. рис.3.15)
Рассмотрим процесс решения задачи оптимизации (8.13). Пусть значения А, В, С, D и К хранятся в ячейках K1:K5. В ячейку B23 введем значение функции At4+Bt3+Ct2+Dt+K в первой точке (ячейка B1):
B23 = $K$1*B1^4 + $K$2*B1^3 + $K$3*B1^2 + $K$4*B1 + $K$5.
Получим ожидаемое значение (в начале 0) в точке B1. Затем растянем эту формулу на весь диапазон B23:J23. В ячейку B24 введем формулу, вычисляющую квадрат разности между экспериментальными и расчетными точками:
B24 = (B23-B2)^2,
и растянем ее на диапазон B24:J24. В ячейке В25 будем хранить суммарную квадратичную ошибку (см. формулу 3.20). Для этого введем формулу:
В25 = СУММ(B24:J24).
Теперь осталось с помощью решающего блока (Данные 
Поиск решения) решить задачу оптимизации без ограничений, заполнив соответствующим образом появившееся диалоговое окно (рис. 3.14).
|
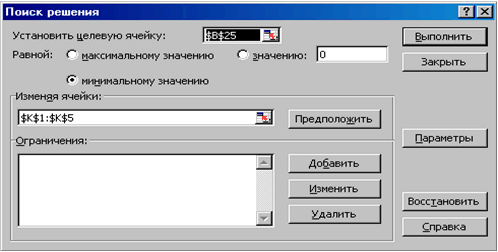
| Рис. 3.14 - Окно поиска решения |
Результатом работы решающего блока будет вывод в ячейки K1:K5 значений параметров функции At4+Bt3+Ct2+Dt+K. В ячейках B23:J23 получим ожидаемые значение функции в исходных точках. Поместим эти точки в виде отдельной линии на графике. В ячейке B25 будет храниться суммарная квадратичная ошибка. Рис. 3.15 отображает внешний вид рабочего листа MS Excel после проведенных вычислений.
Использование решающего блока - это один из эффективных способов реализации метода наименьших квадратов с помощью MS Excel.
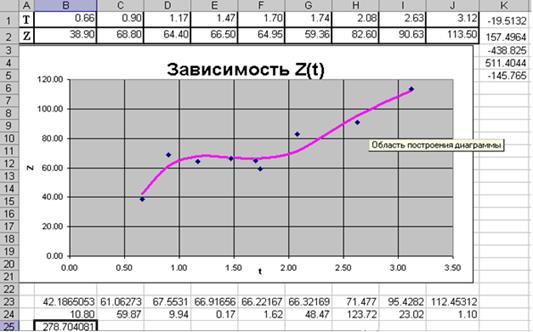
Рис. 3.15 - Графическое представление зависимости
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Получить у преподавателя варианты выполнения двух заданий.
2. На первом рабочем листе документа MS Excel ввести исходные данные, соответствующие варианту задания. Проанализировать экспериментальную зависимость. Построить график экспериментальных точек.
3. На втором рабочем листе средствами MS Excel рассчитать коэффициенты регрессии, коэффициент корреляции, среднеквадратичные отклонения и суммарную ошибку. Построить в одной графической области экспериментальные точки и линию регрессии.
4. Третий рабочий лист должен содержать вычисление коэффициентов функциональной зависимости, соответствующей варианту задания. Расчет коэффициентов произвести аналитически при помощи метода наименьших квадратов, сведя задачу к задаче оптимизации. Построить в одной графической области экспериментальные точки и график подобранной функциональной зависимости. Определить суммарную ошибку.
5. На четвертом рабочем листе построить линию тренда, если это возможно. Убедится в том, что вычисленные в п.3 коэффициенты совпадают с коэффициентами линии тренда. Провести сравнительный анализ полученных результатов и построить в одной графической области график экспериментальных точек, линию регрессии и график полученной экспериментальной зависимости.
6. Озаглавить рабочие листы согласно тематике вычислений. Исходные данные, результаты вычислений и графики сопровождать соответствующими подписями и пояснениями.
7. Подготовить отчет по выполненной работе и представить его преподавателю.
СОДЕРЖАНИЕ ОТЧЕТА
8. Титульный лист.
9. Тема, цель и основное содержание работы.
10. Описание процесса решения задачи.
11. Промежуточные и итоговые результаты.
12. Выводы по работе.
ВАРИАНТЫ ЗАДАНИЙ
Вариант №1. P(s)=As3+Bs2+ С s+D
| S | 0,00 | 1,00 | 1,50 | 2,00 | 2,50 | 3,00 | 3,50 | 4,00 | 4,50 | 5,00 |
| P | 10,00 | 50,10 | 39,58 | 15,40 | 23,68 | 33,60 | 57,78 | 100,90 | 149,50 | 256,00 |
Вариант № 2. G(s)=Aebs
| S | 0,5 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 |
| G | 3,99 | 5,65 | 6,41 | 7,71 | 11,215 | 17,611 | 27,83 | 38,19 | 39,3 |
Вариант № 3. K(s)=Asb
| S | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 |
| K | 1,65 | 2,1 | 2 | 2,1 | 2,3 | 2,4 | 2,22 | 2,59 |
Вариант № 4. V(s)=Asb е Cs
| S | 0,2 | 0,7 | 1,2 | 1,7 | 2,2 | 2,7 | 3,2 |
| V | 2,3198 | 2,9569 | 2,3999 | 6,4357 | 6,5781 | 6,9459 | 14,6621 |
Вариант № 5. W(s)=A/(Bs+C)
| S | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| W | 0,529 | 0,298 | 0,267 | 0,171 | 0,156 | 0,124 | 0,1 | 0,078 | 0,075 |
Вариант № 6. Q(s)=As2+Bs+C
| S | 1 | 1,25 | 1,5 | 1,75 | 2 | 2,25 | 2,5 | 2,75 | 3 |
| Q | 5,21 | 4,196 | 3,759 | 3,672 | 4,592 | 4,621 | 5,758 | 7,173 | 9,269 |
Вариант № 7. Y=x/(Ax-B)
| X | 3 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3,8 | 3,9 |
| Y | 0,61 | 0,6 | 0,592 | 0,58 | 0,585 | 0,583 | 0,582 | 0,57 | 0,572 | 0,571 |
Вариант № 8. V=1/(A+Be-U)
| U | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | 5,5 | 6 |
| V | 5,197 | 7,78 | 11,14 | 15,09 | 19,24 | 23,11 | 26,25 | 28,6 | 30,3 |
Вариант № 9. R=AtB+14,5
| T | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| R | 2,11 | 5,2 | 5,15 | 19,27 | 18,2 | 30,37 | 32 | 31 | 30,22 | 31,2 |
Вариант № 10. R=Ch2+Dh+K
| H | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| R | 0,035 | 0,09 | 0,147 | 0,1 | 0,24 | 0,28 | 0,31 | 0,34 |
Вариант №11. G=DL+K
| L | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 |
| G | 2 | 2,39 | 2,81 | 3,25 | 3,75 | 4,11 | 4,45 | 4,85 | 5,25 |
Лабораторная работа № 4
Оптимизационный анализ в МS Excel
В экономике оптимизационные задачи возникают в связи с многочисленностью различных вариантов функционирования экономического объекта, когда возникает ситуация выбора наилучшего варианта по некоторому критерию. Такие задачи называют задачами линейного программирования (ЗЛП). ЗЛП могут быть использованы в следующих случаях:
- оптимальное использование ресурсов;
- планирование производства;
- оптимальное размещение денежных средств;
- планирование штатного расписания.
Математическая модель ЗЛП в общем виде:
Найти min или max целевой функции
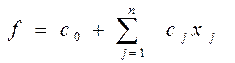
при ограничениях
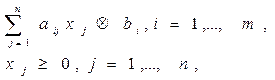
где с0, с j , aij , bi - действительные числа.
Ограничения могут содержать как знаки равенства, так и неравенства.
Транспортная задача — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение. Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки.
Когда суммарный объём предложений (грузов, имеющихся в пунктах отправления) не равен общему объёму спроса на товары (грузы), запрашиваемые пунктами потребления, транспортная задача называется несбалансированной (открытой).
Когда суммарный объем предложения равен объему спроса, транспортная задача закрытого типа или называется закрытой.
Транспортная задача (классическая) — задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределённом количестве) со статичными данными и линеарном подходе (это основные условия задачи).
Для решения таких задач Excel имеет специальный инструмент « Поиск решения». Надстройка «Поиск решения» в Microsoft Excel позволяет напрямую находить оптимальное решение транспортной задачи.
Для добавления надстройки «Поиск решения», если на вкладке «Данные» этого пункта нет перейдите: Файл — Параметры. Слева выберите меню «Надстройки». В основной части выделите «Поиск решения». Затем ниже, нажмите «Перейти». В открывшемся окне отметьте пункт «Поиск решения» и нажмите «Ok». Во вкладке «Данные» появился соответствующий одноименный пункт.
Общее условие транспортной задачи:
Найти m*n неотрицательных чисел Xij– объем перевозок от i-ого поставщика к j-ому потребителю, минимизирующих транспортные затраты по перевозке однородных грузов поставщиков с мощностями (запасами) А1,А2…Ам к потребителям с потребностями В1,В2…Вn, если известны матрица издержек Сij – издержки перевозки единицы груза от i-ого поставщика к j-ому потребителю.
Математическая постановка задачи:
Целевая функция
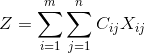
Ограничения
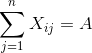для i=1,2….m
При этом необходимо, чтобы транспортная задача была закрытой - суммарная мощность поставщиков должна быть равна суммарной потребности потребителей.
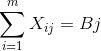для j=1,2….n
Если задача открытого типа, для балансирования суммарных запасов и потребностей вводится или фиктивный поставщик, запасы которого равны превышению суммарных потребностей над суммарными запасами, или фиктивный потребитель, потребности которого равны превышению суммарных запасов над суммарными потребностями. При этом матрица издержек дополняется строкой или столбцом с нулевыми элементами.
Примеры решения оптимизационных задач в MS EXCEL
Постановка задачи о планировании производства
Небольшая фабрика выпускает 2 вида товаров. Для производства товаров используется два исходных продукта А и В. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 тонн соответственно. Данные по производству товаров приведены в таблице 4.1.
Таблица 4.1 - Исходные данные задачи
| Исходный продукт | расход исходного продукта на 1 тонну товара | Максимально возможный запас | |
| товар 1 | товар 2 | ||
| А | 1 | 2 | 6 |
| В | 2 | 1 | 8 |
Изучение рынка сбыта показало, что суточный спрос на товар 1 никогда не превышает спрос на товар 2 на 1 тонну. Установлено, что спрос на товар 1 никогда не превышает 2 тонны в сутки. Цена товара 1 – 3000 руб, товара 2 – 2000 рублей.
Какое количество товаров должна производить фабрика, чтобы максимизировать свою прибыль.
Математическая постановка задачи:
Переменные:
Х1 – количество товара 1, Х2 – количество товара 2 (в тоннах).
Целевая функция:
f(x) = 3000*X1 + 2000*X2 ® max
Ограничения:
Х1 + 2*Х2 £ 6;
2*Х1 + Х2 £ 8;
Х1, Х2 ³ 0;
Х1 – Х2 £ 1;
Х1£ 2.
Технология решения задачи
1. Разработайте шаблон для решения задачи. Для этого в ячейку А1 запишите “Переменные”; в ячейку А2 -“Х1”, в В2 – “Х2”; в А4 – “Функция цели”; в С4 – формулу “=3000*А3 + 2000*В3”; в А6 – “Ограничения”; в А7 – “=А3 + 2*В3”; А8 – “=2*А3 + В3”; А9 – “=В3-А3”; А10 – “=В3”; в В7 – “6”; в В8 – “8”; в В9 – “1”; в В10 – “2”.
2. Установите надстройку «Поиск решения» - Главная кнопка – Параметры - Надстройки – Поиск решения – Перейти - ОК. Выполните команду ДАННЫЕ – ПОИСК РЕШЕНИЯ, На экране отобразится диалоговое окно Поиск решения (рис.4.1). Заполните его в соответствии с приведенным рисунком.
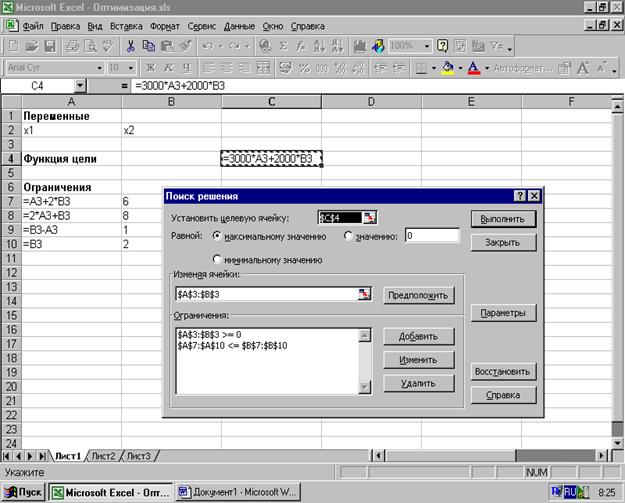
Рис. 4.1. Решение задачи с помощью средства Поиск решения.
3. Нажмите кнопку Параметры. На экране отобразится диалоговое окно Параметры поиска решения. В диалоговом окне можно изменять условия и варианты поиска решения исследуемой задачи, а также загружать и сохранять оптимизируемые модели. В нашей задаче оставим все параметры, установленные по умолчанию, предварительно установив флажок Линейная модель.
4. Нажмите кнопку Выполнить. На экране отобразится окно Результаты поиска решения.
Поиск решения нашел оптимальный план производства товаров, дающий максимальную прибыль. Оптимальным является производство в сутки 3 1/3 товара 1 и 1 1/3 товара 2. Этот объем производства принесет 12 1/3 тыс. руб. прибыли.
Дата: 2018-11-18, просмотров: 658.
