Этот инструмент предназначен для автоматической генерации множества данных (генеральной совокупности) заданного объема, элементы которого характеризуются определенным распределением вероятностей. При этом могут быть использованы 7 типов распределений: равномерное, нормальное, Бернулли, Пуассона, биномиальное, модельное и дискретное. Применение инструмента "Генератор случайных чисел", как и большинства используемых в этой работе функций, требует установки специального дополнения "Пакет анализа" (см лабораторную работу № 1).
Для демонстрации техники применения этого инструмента изменим условия примера, рассмотренного в предыдущей лабораторной работе, определив вероятности для каждого сценария развития событий следующим образом (таблица 2.1). Мы также будем исходить из предположения о нормальном распределении ключевых переменных. Количество имитаций оставим прежним - 500.
Таблица 2.1 - Вероятностные сценарии реализации проекта
| Показатели | Наихудший P = 0.25 | Наилучший P = 0.25 | Вероятный P = 0.5 |
| Объем выпуска Q | 150 | 300 | 200 |
| Цена за штуку P | 40 | 55 | 50 |
| Переменные затраты V | 35 | 25 | 30 |
Приступим к формированию шаблона. Как и в предыдущем случае, выделим в рабочей книге два листа: "Имитация" и "Результаты анализа".
Формирование шаблона целесообразно начать с листа "Результаты анализа" (рисунок 2.1).
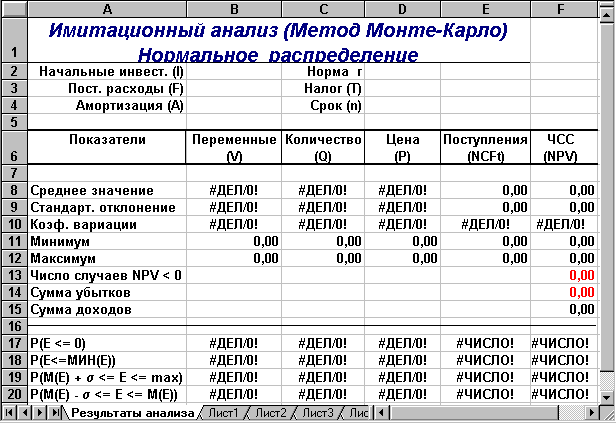
Рис. 2.1. Лист "Результаты анализа" (шаблон II)
Как следует из рисунка 2.1, этот лист практически соответствует ранее разработанному для решения предыдущей задачи (см. лабораторную работу № 3). Отличие составляют лишь формулы для расчета вероятностей, которые приведены в таблице 2.2.
Таблица 2.2 - Формулы листа "Результаты анализа" (шаблон II)
| Ячейка | Формула |
| 1 | 2 |
| В17 | =НОРМРАСП(0;B8;B9;1) |
| В18 | =НОРМРАСП(B11;B8;B9;1) |
| В19 | =НОРМРАСП(B12;B8;B9;1)-НОРМРАСП(B8+B9;B8;B9;1) |
| В20 | =НОРМРАСП(B8;B8;B9;1)-НОРМРАСП(B8-B9;B8;B9;1) |
Окончание таблицы 2.2
| 1 | 2 |
| С17 | =НОРМРАСП(0;C8;C9;1) |
| С18 | =НОРМРАСП(C11;C8;C9;1) |
| С19 | =НОРМРАСП(C12;C8;C9;1)-НОРМРАСП(C8+C9;C8;C9;1) |
| С20 | =НОРМРАСП(C8;C8;C9;1)-НОРМРАСП(C8-C9;C8;C9;1) |
| D17 | =НОРМРАСП(0;D8;D9;1) |
| D18 | =НОРМРАСП(D11;D8;D9;1) |
| D19 | =НОРМРАСП(D12;D8;D9;1)-НОРМРАСП(D8+D9;D8;D9;1) |
| D20 | =НОРМРАСП(D8;D8;D9;1)-НОРМРАСП(D8-D9;D8;D9;1) |
| E17 | =НОРМРАСП(0;E8;E9;1) |
| E18 | =НОРМРАСП(E11;E8;E9;1) |
| E19 | =НОРМРАСП(E12;E8;E9;1)-НОРМРАСП(E8+E9;E8;E9;1) |
| E20 | =НОРМРАСП(E8;E8;E9;1)-НОРМРАСП(E8-E9;E8;E9;1) |
| F17 | =НОРМРАСП(0;F8;F9;1) |
| F18 | =НОРМРАСП(F11;F8;F9;1) |
| F19 | =НОРМРАСП(F12;F8;F9;1)-НОРМРАСП(F8+F9;F8;F9;1) |
| F20 | =НОРМРАСП(F8;F8;F9;1)-НОРМРАСП(F8-F9;F8;F9;1) |
Используемые в нем собственные имена ячеек также взяты из аналогичного листа предыдущего шаблона (см. лабораторную работу № 1).
Для быстрого формирования нового листа "Результаты анализа" выполните следующие действия.
1 Загрузите предыдущий шаблон SIMUL_1 и сохраните его под другим именем, например - SIMUL_2
2. Удалите лист "Имитация".
3. Перейдите в лист "Результаты анализа". Удалите строки 17-18. Откорректируйте заголовок.
4. Добавьте формулы из таблицы 2.1. Для этого введите соответствующие формулы в ячейки блока В17:В20 и скопируйте их в блок С17:F20. Введите соответствующие комментарии.
5. Сверьте полученную таблицу с рисунком 2.1.
6. Перейдите к следующему листу и присвойте ему имя "Имитация". Приступаем к его формированию (рис. 2.2).
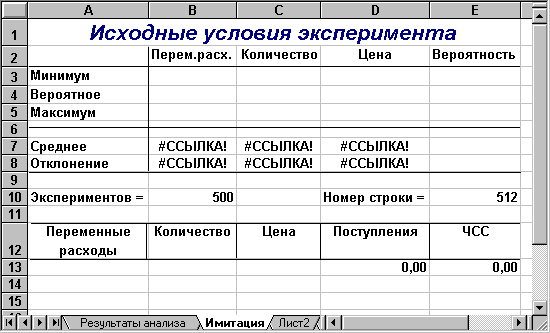
Рис. 2.2. Лист "Имитация" (шаблон II)
Первая часть этого листа (блок ячеек А1:Е10) предназначена для ввода исходных данных и расчета необходимых параметров их распределений. Напомним, что нормальное распределение случайной величины характеризуется двумя параметрами - математическим ожиданием (средним) и стандартным отклонением. Для удобства определения формул и повышения их наглядности блоку ячеек Е3:Е5 присвоено имя "Вероятности" (см. таблицу 2.3). Остальные имена остаются как в предыдущей лабораторной работе. Формулы расчета указанных параметров для ключевых переменных модели заданы в блоках ячеек В7:D7 и B8:D8 соответственно (см. таблицу 2.4).
Таблица 2.3 - Имена ячеек листа "Имитация" (шаблон II)
| Адрес ячейки | Имя | Комментарии |
| Блок Е3:Е5 | Вероятности | Вероятность значения параметра |
| Блок A13:A512 | Перем_расх | Переменные расходы |
| Блок B13:B512 | Количество | Объем выпуска |
| Блок C13:C512 | Цена | Цена изделия |
| Блок D13:D512 | Поступления | Поступления от проекта NCF |
| Блок E13:E512 | ЧСС | Чистая современная стоимость NPV |
Таблица 2.4 - Формулы листа "Имитация" (шаблон II)
| Ячейка | Формула |
| В7 | =СУММПРОИЗВ(B3:B5; Вероятности) |
| В8 | {=КОРЕНЬ(СУММПРОИЗВ((B3:B5 - B7)^2; Вероятности))} |
| С7 | =СУММПРОИЗВ(C3:C5; Вероятности) |
| С8 | {=КОРЕНЬ(СУММПРОИЗВ((C3:C5 - C7)^2; Вероятности))} |
| D7 | =СУММПРОИЗВ(D3:D5; Вероятности) |
| D8 | {=КОРЕНЬ(СУММПРОИЗВ((D3:D5 - D7)^2; Вероятности))} |
| E10 | =B10+13 -1 |
| D13 | =(B13*(C13-A13)-Пост_расх-Аморт)*(1-Налог)+Аморт |
| E13 | =ПС(Норма; Срок; -D13) - Нач_инвест |
Обратите внимание на то, что для расчета стандартных отклонений используются формулы-массивы. Для формирования блока формул достаточно определить их для ячеек В7:В8 и затем скопировать в блок С7:D8.
Формула в ячейке Е10 по заданному числу имитаций (ячейка В10) вычисляет номер последней строки для блоков, в которых будут храниться сгенерированные значения ключевых переменных.
Ячейки D13:E13 содержат уже знакомые нам формулы для расчета величины потока платежей NCF и его чистой современной стоимости NPV.
Сформируйте элементы оформления листа "Имитация", определите необходимые имена для блоков ячеек (таблица 2.3) и задайте требуемые формулы (таблица 4.3). Сверьте полученную ЭТ с рисунком 2.2. Сохраните полученный шаблон под именем SIMUL_2.
Введите исходные значения постоянных переменных (лабораторная работа № 1) в ячейки В2:В4 и D2:D4 листа "Результаты анализа". Перейдите к листу "Имитация". Введите значения ключевых переменных и соответствующие вероятности (таблица 2.1). Полученная в результате ЭТ должна иметь вид, как рисунке 2.3.
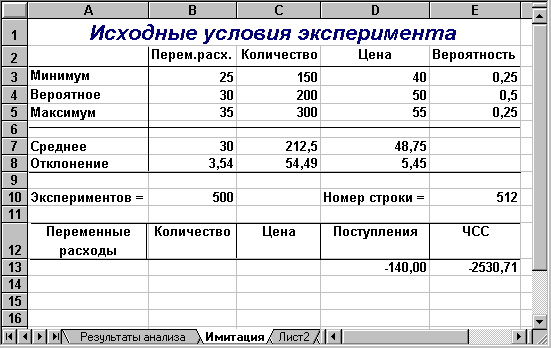
Рис. 2.3. Лист "Имитация" после ввода исходных данных
Установите курсор в ячейку А13. Приступаем к проведению имитационного эксперимента.
1. Выберите команду ДАННЫЕ -"Анализ данных". Результатом выполнения этих действий будет появление диалогового окна "Анализ данных", содержащего список инструментов анализа.
2. Выберите из списка "Инструменты анализа" пункт "Генерация случайных чисел" и нажмите кнопку "ОК" (рисунок 2.4). На экране появится диалоговое окно "Генерация случайных чисел". Укажите в списке "Распределения" требуемый тип - "Нормальное". Заполните остальные поля изменившегося окна согласно рисунку 2.5 и нажмите кнопку "ОК". Результатом будет заполнение блока ячеек А13:А512 (переменные расходы) сгенерированными случайными значениями.

Рис. 2.4. Выбор инструмента "Генерация случайных чисел"
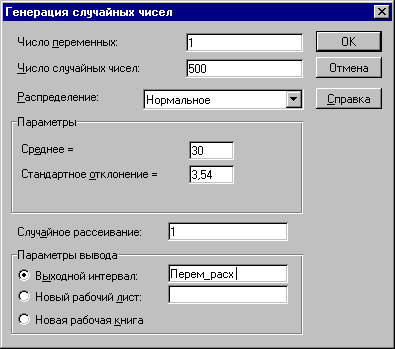
Рис.2.5. Заполнение полей окна "Генерация случайных чисел"
Приведем необходимые пояснения. Первым заполняемым аргументом диалогового окна "Генерация случайных чисел" является поле "Число переменных". Оно задает количество колонок ЭТ, в которых будут размещаться сгенерированные в соответствии с заданным законом распределения случайные величины. В нашем примере оно должно содержать 1, так как ранее мы отвели под значения переменной V (переменные расходы) в ЭТ одну колонку - "А". В случае, если указывается число больше 1, случайные величины будут размещены в соответствующем количестве соседних колонок, начиная с активной ячейки. Если это число не введено, то все колонки в выходном диапазоне будут заполнены.
Следующим обязательным аргументом для заполнения является содержимое поля "Число случайных чисел" (т.е. количество имитаций). Согласно условиям примера оно должно быть равно 500. При этом ППП EXCEL автоматически подсчитывает необходимое количество ячеек для хранения генеральной совокупности.
Необходимый вид распределения задается путем соответствующего выбора из списка "Распределения". Как уже отмечалось ранее, могут быть получены 7 наиболее распространенных в практическом анализе типов распределений, каждое из которых характеризуется собственными параметрами. Выбранный тип распределения определяет внешний вид диалогового окна. В рассматриваемом примере выбор типа распределения "Нормальное" повлек за собой появление дополнительных аргументов - его параметров "Среднее" и "Стандартное отклонение", рассчитанных ранее для исследуемой переменной V в ячейках В7 и В8 листа "Имитация". К сожалению эти аргументы могут быть заданы только в виде констант. Использование адресов ячеек и собственных имен здесь не допускается!
Указание аргумента "Случайное рассеивание" позволяет при повторных запусках генератора получать те же значения случайных величин, что и при первом. Таким образом, одну и ту же генеральную совокупность случайных чисел можно получить несколько раз, что значительно повышает эффективность анализа (сравните с предыдущим шаблоном!). В случае если этот аргумент не задан (равен 0), при каждом последующем запуске генератора будет формироваться новая генеральная совокупность. В нашем примере этот аргумент задан равным 1, что позволит нам оперировать с одной и той же генеральной совокупностью и избежать постоянных перерасчетов ЭТ.
Последний аргумент диалогового окна "Генерация случайных чисел" - "Параметры вывода" определяет место расположения полученных результатов. Место вывода задается путем установления соответствующего флажка. При этом можно выбрать три варианта размещения:
- выходной блок ячеек на текущем листе - введите ссылку на левую верхнюю ячейку выходного диапазона, при этом его размер будет определен автоматически и в случае возможного наложения генерируемых значений на уже имеющиеся данные на экран будет выведено предупреждающее сообщение;
- новый рабочий лист - в рабочей книге будет открыт новый лист, содержащий результаты генерации случайных величин, начиная с ячейки A1;
- новая рабочая книга - будет открыта новая книга с результатами имитации на первом листе.
В рассматриваемом примере для проведения дальнейшего анализа необходимо, чтобы случайные величины размещались в специально отведенные для них блоки ячеек. В частности для хранения 500 значений первой переменной ранее был отведен блок ячеек А13:А512. Поскольку для этого блока определено собственной имя - "Перем_расх", оно указано в качестве выходного диапазона. Отметим, что при увеличении либо уменьшении количества имитаций необходимо также переопределить и выходные блоки, предназначенные для хранения значений переменных.
Генерация значений остальных переменных Q и Р осуществляется аналогичным образом, путем выполнения шагов 1-3. Пример заполнения окна "Генерация случайных чисел" для переменной Q (количество) приведен на рисунке 2.6.
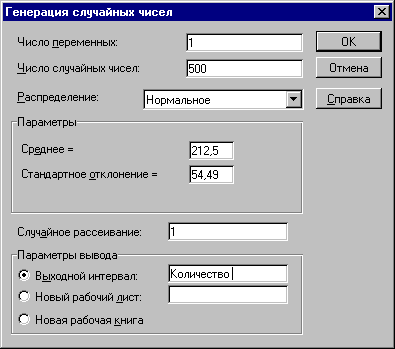
Рис.2.6. Заполнение полей окна для переменной Q
Для получения генеральной совокупности значений потока платежей и их чистой современной стоимости необходимо скопировать формулы базовой строки (ячейки D13:E13) требуемое число раз (499).
Полученные результаты решения примера приведены на рисунках 2.7 и 2.8.
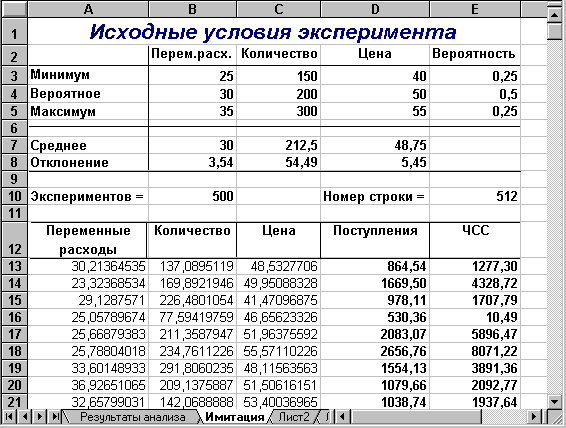
Рис. 2.7. Результаты имитационного эксперимента (шаблон II)
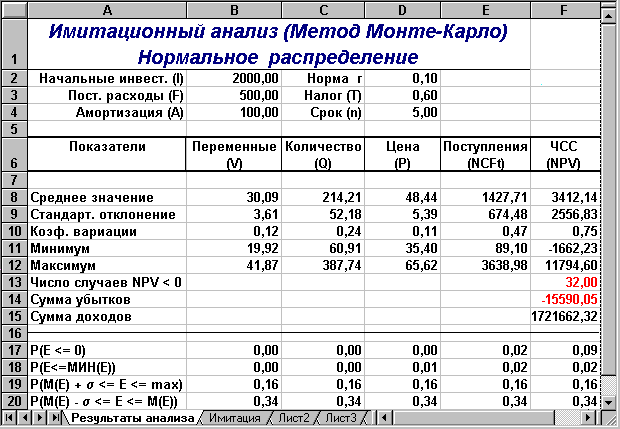
Рис.2.8. Результаты анализа (шаблон II)
Инструмент анализа данных "Описательная статистика"
Чем больше характеристик распределения случайной величины нам известно, тем точнее мы можем судить об описываемых ею процессов. Инструмент "Описательная статистика" автоматически вычисляет наиболее широко используемые в практическом анализе характеристики распределений. При этом значения могут быть определены сразу для нескольких исследуемых переменных.
Определим параметры описательной статистики для переменных V, Q, P, NCF, NPV. Для этого необходимо выполнить следующие шаги.
1. "Анализ данных". Выберите из списка "Инструменты анализа" пункт "Описательная статистика".
2. Заполните поля диалогового окна, как показано на рисунке 3.4 и нажмите кнопку "ОК".
Результатом выполнения указанных действий будет формирование отдельного листа, содержащего вычисленные характеристики описательной статистики для исследуемых переменных. Выполнив операции форматирования, можно привести полученную ЭТ к более наглядному виду (рисунок 3.5).
Многие из приведенных в данной ЭТ характеристик вам уже хорошо знакомы, а их значения уже определены с помощью соответствующих функций на листе "Результаты анализа". Поэтому рассмотрим лишь те из них, которые не упоминались ранее.
Вторая строка ЭТ содержит значения стандартных ошибок e для средних величин распределений. Другими словами среднее или ожидаемое значение случайной величины М(Е) определено с погрешностью ± e .
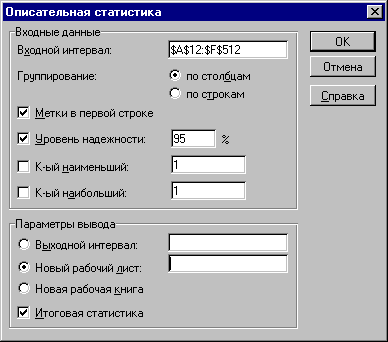
Рис. 3.4. Заполнение полей диалогового окна "Описательная статистика"

Рис.3.5. Описательная статистика для исследуемых переменных
Медиана - это значение случайной величины, которое делит площадь, ограниченную кривой распределения, пополам (т.е. середина численного ряда или интервала). Как и математическое ожидание, медиана является одной из характеристик центра распределения случайной величины. В симметричных распределениях значение медианы должно быть равным или достаточно близким к математическому ожиданию.
Как следует из полученных результатов, данное условие соблюдается для исходных переменных V, Q, P (значения медиан лежат в диапазоне М(Е) ± e , т.е. - практически совпадают со средними). Однако для результатных переменных NCF, NPV значения медиан лежат ниже средних, что наводит на мысль о правосторонней асимметричности их распределений.
Мода - наиболее вероятное значение случайной величины (наиболее часто встречающееся значение в интервале данных). Для симметричных распределений мода равна математическому ожиданию. Иногда мода может отсутствовать. В данном случае ППП EXCEL вернул сообщение об ошибке. Таким образом, вычисление моды не представляется возможным.
Эксцесс характеризует остроконечность (положительное значение) или пологость (отрицательное значение) распределения по сравнению с нормальной кривой. Теоретически, эксцесс нормального распределения должен быть равен 0. Однако на практике для генеральных совокупностей больших объемов его малыми значениями можно пренебречь.
В рассматриваемом примере примерно одинаковый положительный эксцесс наблюдается у распределений переменных Q, NCF, NPV. Таким образом графики этих распределений будут чуть остроконечнее, по сравнению с нормальной кривой. Соответственно графики распределений для переменных V и Р будут чуть более пологими, по отношению к нормальному.
Асимметричность (коэффициент асимметрии или скоса - s) характеризует смещение распределения относительно математического ожидания. При положительном значении коэффициента распределение скошено вправо, т.е. его более длинная часть лежит правее центра (математического ожидания) и обратно. Для нормального распределения коэффициент асимметрии равен 0. На практике, его малыми значениями можно пренебречь.
В частности асимметрию распределений переменных V, Q, P в данном случае можно считать несущественной, чего нельзя однако сказать о распределении величины NPV.
Осуществим оценку значимости коэффициента асимметрии для распределения NPV. Наиболее простым способом получения такой оценки является определение стандартной (средней квадратической) ошибки асимметрии, рассчитываемой по формуле:
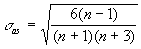
где n - число значений случайной величины (в данном случае 500).
Если отношение коэффициента асимметрии s к величине ошибки s as меньше трех (т.е.: s /s as < 3), то асимметрия считается несущественной, а ее наличие объясняется воздействием случайных факторов. В противном случае асимметрия статистически значима и факт ее наличия требует дополнительной интерпретации. Осуществим оценку значимости коэффициента асимметрии для рассматриваемого примера.
Введите в любую ячейку ЭТ формулу:
= 0,763 / КОРЕНЬ(6*499 / 501*503) (Результат: 7,06).
Поскольку отношение s /s as > 3, асимметрию следует считать существенной. Таким образом наше первоначальное предположение о правосторонней скошенности распределения NPV подтвердилась.
Для рассматриваемого примера наличие правосторонней асимметрии может считаться положительным моментом, так как это означает, что большая часть распределения лежит выше математического ожидания, т.е. большие значения NPV являются более вероятными.
Аналогичным способом можно осуществить проверку значимости величины эксцесса е. Формула для расчета стандартной ошибки эксцесса имеет следующий вид:
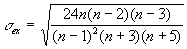
где n - число значений случайной величины.
Если отношение e /s ex < 3, эксцесс считается незначительным и его величиной можно пренебречь.
Величина "Интервал" определяется как разность между максимальным и минимальным значением случайной величины (численного ряда). Параметры "Счет" и "Сумма" представляют собой число значений в заданном интервале и их сумму соответственно.
Последняя характеристика "Уровень надежности" показывает величину доверительного интервала для математического ожидания согласно заданному уровню надежности или доверия. По умолчанию уровень надежности принят равным 95%.
Для рассматриваемого примера это означает, что с вероятностью 0,95 (95%) величина математического ожидания NPV попадет в интервал 3412,14 ± 224,88.
Вы можете указать другой уровень надежности, например - 98%, путем ввода соответствующего значения в поле "Уровень надежности" диалогового окна "Описательная статистика". Следует отметить, что чем выше принятый уровень надежности, тем больше будет величина доверительного интервала для среднего.
В заключении отметим, что имитационное моделирование позволяет учесть максимально возможное число факторов внешней среды для поддержки принятия управленческих решений и является наиболее мощным средством анализа инвестиционных рисков. Необходимость его применения в отечественной финансовой практике обусловлена особенностями российского рынка, характеризующегося субъективизмом, зависимостью от внеэкономических факторов и высокой степенью неопределенности.
Результаты имитации могут быть дополнены вероятностным и статистическим анализом и в целом обеспечивают менеджера наиболее полной информацией о степени влияния ключевых факторов на ожидаемые результаты и возможных сценариях развития событий.
Задание к лабораторной работе № 2
1. Постройте модель из теоретической части, проведите с ней эксперименты.
2. Используйте варианты индивидуальных заданий для постановки данных в построенную модель
3. С использованием инструмента «Описательная статистика» получите дополнительные статистические данные
4. Постройте отчет, куда включите фрагмент листа «Имитация» - первые 40 экспериментов, полностью лист «Результаты анализа» и «Описательная статистика». Прокомментируйте каждый показатель этого листа с точки зрения оценивания риска инвестиционного проекта.
Лабораторная работа № 3
Дата: 2018-11-18, просмотров: 478.