Для точного расчета необходимо знать ДН с учетом направленных свойств одного элемента. Однако в случае достаточно длинных антенн ДН решетки в основном определяется множителем системы. Рассмотрим решетку с произвольным амплитудным распределением токов по закону
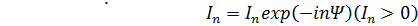 .
.
Для расчета КНД в направлении 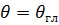 справедлива формула
справедлива формула
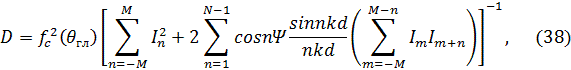
где 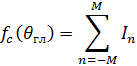 при
при 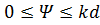 ,
,
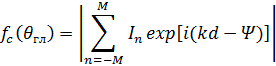 при
при 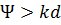 .
.
Рассмотрим синфазный равноамплитудный режим (Ψ=0, 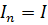 ,
, 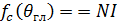 ). Результаты расчета по формуле (38) показывают, что практически при любом фиксированном числе излучающих элементов N максимум КНД наблюдается при
). Результаты расчета по формуле (38) показывают, что практически при любом фиксированном числе излучающих элементов N максимум КНД наблюдается при 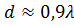 . При дальнейшем увеличении расстояния между элементами КНД уменьшается в связи с появлением (при
. При дальнейшем увеличении расстояния между элементами КНД уменьшается в связи с появлением (при 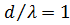 ) дополнительных главных максимумов. Однако если задана длина решетки
) дополнительных главных максимумов. Однако если задана длина решетки 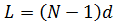 (для длинных антенн
(для длинных антенн 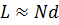 ), то для получения максимума КНД более целесообразно выбирать
), то для получения максимума КНД более целесообразно выбирать 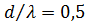 . При таком значении шага УБЛ убывает при удалении от направления максимума излучения. Кроме того, при дальнейшем уменьшении d КНД остается практически неизменным. При
. При таком значении шага УБЛ убывает при удалении от направления максимума излучения. Кроме того, при дальнейшем уменьшении d КНД остается практически неизменным. При 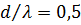 , учитывая, что
, учитывая, что 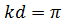 ,
, 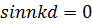 , из (38) получаем
, из (38) получаем
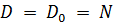 . (39)
. (39)
Этот же результат можно объяснить тем, что для изотропных элементов при d, кратных λ/2, активная часть взаимных сопротивлений обращается в нуль и при фиксированном значении мощность 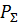 делится поровну между всеми элементами. При этом ток в каждом элементе будет в
делится поровну между всеми элементами. При этом ток в каждом элементе будет в 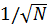 раз меньше, чем ток в одном элементе, излучающем ту же мощность
раз меньше, чем ток в одном элементе, излучающем ту же мощность 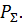
Суммарное поле в направлении максимума будет превышать поле одного элемента в 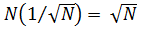 раз, соответственно КНД решетки возрастет в N раз. Для длинных решеток
раз, соответственно КНД решетки возрастет в N раз. Для длинных решеток 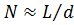 , поэтому
, поэтому
D0= 2L / λ . (40)
Перейдем к режиму осевого излучения, когда 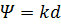 . При значении
. При значении 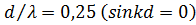 , что соответствует убывающему закону изменения УБЛ, величина КНД, как и в предыдущем случае, равна N. Однако теперь шаг решетки в 2 раза меньше, так что
, что соответствует убывающему закону изменения УБЛ, величина КНД, как и в предыдущем случае, равна N. Однако теперь шаг решетки в 2 раза меньше, так что
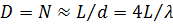 . (41)
. (41)
Таким образом, при одной и той же длине антенны L в режиме осевого излучения при 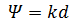 значение КНД можно получить в 2 раза больше, чем в режиме нормального излучения.
значение КНД можно получить в 2 раза больше, чем в режиме нормального излучения.
Анализ формулы (38) показывает, что при 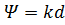 наблюдается сначала дальнейший рост КНД, а затем его резкое снижение. Сказанное справедливо при шаге решетки
наблюдается сначала дальнейший рост КНД, а затем его резкое снижение. Сказанное справедливо при шаге решетки 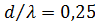 . В оптимальном режиме, соответствующем максимуму КНД, при
. В оптимальном режиме, соответствующем максимуму КНД, при 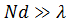
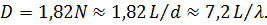 (42)
(42)
Общий вид поведения КНД равноамплитудной АР в зависимости от 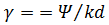 при
при 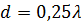 представлен графиком на рис. 11 (сплошная линия). Обратим внимание на практически постоянное значение КНД на начальном участке графика, т.е. в режиме наклонного излучения. Это объясняется тем, что расширение главного лепестка при его отклонении от нормали компенсируется уменьшением телесного угла, занимаемого данным лепестком, поскольку он приобретает в пространстве воронкообразную форму (см. рис. 6).
представлен графиком на рис. 11 (сплошная линия). Обратим внимание на практически постоянное значение КНД на начальном участке графика, т.е. в режиме наклонного излучения. Это объясняется тем, что расширение главного лепестка при его отклонении от нормали компенсируется уменьшением телесного угла, занимаемого данным лепестком, поскольку он приобретает в пространстве воронкообразную форму (см. рис. 6).
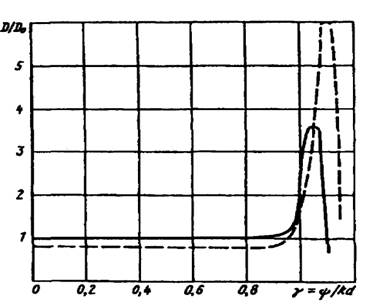
Рисунок 11. КНД равноамплитудной АР в зависимости от 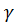 при
при 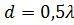
Перейдем теперь к амплитудным распределениям, спадающим к краям решетки. В синфазном режиме (Ψ = 0) при 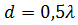 из (38) получим
из (38) получим
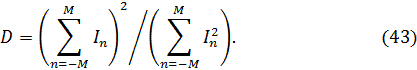
Из сравнения с (39) имеем
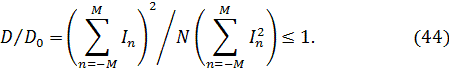
Отношение (44) называется коэффициентом использования линейной АР ( 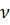 ), который учитывает снижение КНД при спадающем амплитудном распределении по сравнению с синфазным равноамплитудным возбуждением. При известном коэффициенте
), который учитывает снижение КНД при спадающем амплитудном распределении по сравнению с синфазным равноамплитудным возбуждением. При известном коэффициенте 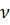
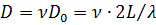 . (45)
. (45)
Таким образом, можно сделать следующие выводы. Линейные решетки с равноамплитудным возбуждением имеют максимальное значение КНД по сравнению с другими типами рассмотренных выше распределений в режиме нормального излучения. В режиме осевого излучения больший КНД имеют решетки с неравномерным амплитудным распределением спадающим к краям.
Все сказанное справедливо, если поля отдельных элементов в главном направлении складываются синфазно или с малым фазовым сдвигом. В противном случае, когда формирование диаграммы во всех направлениях, в том числе в направлении главного максимума, осуществляется на разностном эффекте, теоретически возможно достижение существенно большей направленности, однако использование подобных решений (так называемых «сверхнаправленных» или «реактивных» антенн) встречает практически непреодолимые трудности из-за резкого возрастания амплитуд токов. Отметим, что увеличение амплитуд токов (приемлемое, однако, с практической точки зрения) начинает проявляться уже в АР с осевым излучением в оптимальном режиме с равномерным распределением токов, тем более при спадании их к краям решетки.
Фазовые ошибки, как квадратичные, так и кубические, приводят к снижению КНД. Степень снижения КНД зависит помимо величины ошибки также от типа амплитудного распределения. Если амплитудное распределение спадает к краям решетки, то при прочих равных условиях влияние фазовых ошибок уменьшается, так как снижается вклад в результирующее поле от наиболее расфазированных крайних элементов.
Плоские антенные решетки
Рассмотренные ранее линейные АР в режимах нормального и наклонного излучений позволяют сформировать направленное излучение только в одной плоскости, проходящей через ось решетки. Плоские АР дают возможность сконцентрировать излучение в узкий пучок в двух плоскостях. Форма плоской АР (форма раскрыва решетки) может быть прямоугольной, круглой, шестиугольной и т.д. и определяется как требованиями, предъявляемыми к форме ДН, так и конструктивными особенностями системы. Излучатели в плоских АР располагаются в узлах прямоугольной или треугольной (гексагональной) сетки (рис. 14).
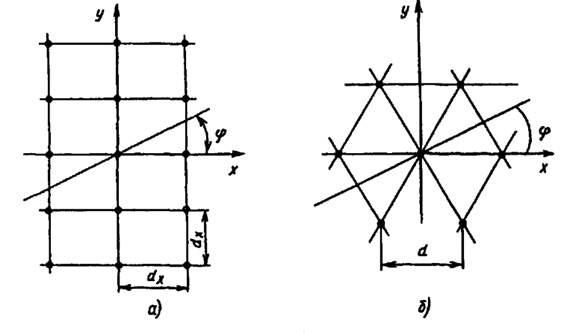
Рисунок 14. Положение излучателей в плоских AР
Рассмотрим подробнее излучение плоской АР прямоугольной формы с расположением изотропных излучателей в плоскости 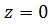 в узлах прямоугольной сетки. Пусть решетка состоит из
в узлах прямоугольной сетки. Пусть решетка состоит из 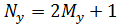 рядов излучателей, параллельных оси у, причем расстояние между рядами равно
рядов излучателей, параллельных оси у, причем расстояние между рядами равно 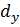 . Каждый ряд состоит из
. Каждый ряд состоит из 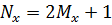 излучателей с шагом
излучателей с шагом 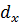 . Координаты излучателей в плоскости решетки определяются как
. Координаты излучателей в плоскости решетки определяются как 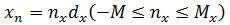 и
и 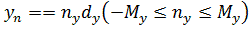 . Тогда множитель системы примет вид
. Тогда множитель системы примет вид
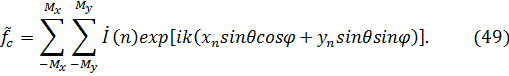
Наиболее простым является случай, когда распределение тока может быть представлено в виде произведения двух функций, зависящих только от х и только от у
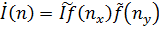 . (50)
. (50)
Пусть решетка возбуждается равноамплитудно. Тогда амплитудный множитель имеет вид, справедливый для произвольной плоскости 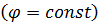 , проходящей через нормаль к плоскости решетки:
, проходящей через нормаль к плоскости решетки:
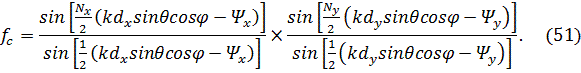
Можно показать, что каждый из сомножителей в (51) соответствует множителю системы линейной АР, ориентированной вдоль осей х или у. Такие же выводы справедливы для любых распределений возбуждающего тока, представленных в виде функций, разделяющихся по координатам х и у.
При 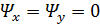 (синфазная решетка) максимум излучения ориентирован по нормали к плоскости решетки (рис. 15, а). Излучение в нижнее полупространство устраняется обычно либо выбором однонаправленных излучающих элементов, либо с помощью экранов (рис. 15, б). Форма ДН в каждой из главных плоскостей ( x 0 z и у0 z ) определяется только геометрией решетки в этой плоскости и амплитудно-фазовым распределением в этой же плоскости.
(синфазная решетка) максимум излучения ориентирован по нормали к плоскости решетки (рис. 15, а). Излучение в нижнее полупространство устраняется обычно либо выбором однонаправленных излучающих элементов, либо с помощью экранов (рис. 15, б). Форма ДН в каждой из главных плоскостей ( x 0 z и у0 z ) определяется только геометрией решетки в этой плоскости и амплитудно-фазовым распределением в этой же плоскости.
При линейном фазовом распределении, когда 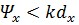 и
и 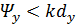 (что характерно для плоских АР), направление максимума основного лепестка (
(что характерно для плоских АР), направление максимума основного лепестка ( 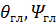 ) определяется из условий равенства нулю числителей обоих сомножителей в (51):
) определяется из условий равенства нулю числителей обоих сомножителей в (51):
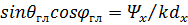 ,
, 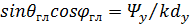 . (52)
. (52)
откуда получаем соотношения, справедливые при любом амплитудном распределении:
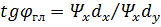 ,
, 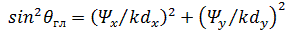 . (53)
. (53)
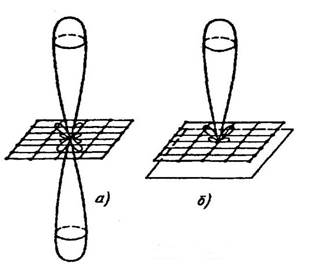
Рисунок 15. Направление максимума излучения синфазной решетки
Для расчета ДН в произвольной плоскости помимо выражений типа (51) могут быть также использованы результаты теории линейных АР. Достигается это введением понятия эквивалентной линейной решетки. Рассмотрим для примера ДН квадратной решетки с шагом 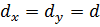 в плоскости, след которой, составляющий угол
в плоскости, след которой, составляющий угол 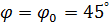 с осью х, на рис. 16 обозначен s - s (диагональная плоскость).
с осью х, на рис. 16 обозначен s - s (диагональная плоскость).
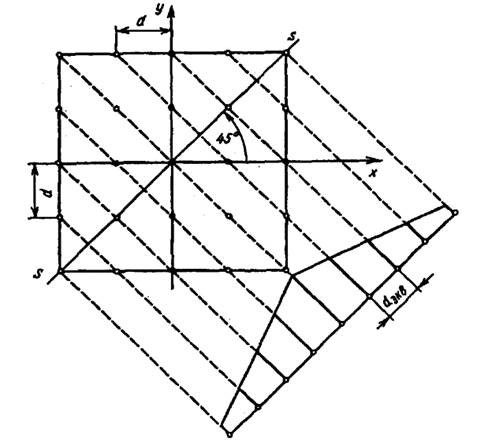
Рисунок 16. Пример ДН квадратной решетки
Пусть элементы решетки возбуждаются синфазно и равноамплитудно ( 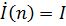 ). Проведем через точки расположения излучателей штриховые линии, перпендикулярные следу s - s. Для любой точки наблюдения в интересующей нас плоскости в дальней зоне излучатели, лежащие на одной из этих линий (обозначим число таких излучателей через n), равноудалены, соответственно поля их складываются синфазно. Поэтому при вычислении ДН плоской решетки в плоскости s - s действие всех излучателей можно заменить излучением одного эквивалентного элемента с током mI , расположенного в любой точке штриховой линии.
). Проведем через точки расположения излучателей штриховые линии, перпендикулярные следу s - s. Для любой точки наблюдения в интересующей нас плоскости в дальней зоне излучатели, лежащие на одной из этих линий (обозначим число таких излучателей через n), равноудалены, соответственно поля их складываются синфазно. Поэтому при вычислении ДН плоской решетки в плоскости s - s действие всех излучателей можно заменить излучением одного эквивалентного элемента с током mI , расположенного в любой точке штриховой линии.
На рис. 16 для удобства эквивалентные излучатели изображены на прямой вне плоскости решетки. Совокупность таких эквивален тных элементов и образует эквивалентную линейную решетку с шагом 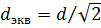 . Длина эквивалентной решетки в рассматриваемом случае равна диагонали квадрата, а распределение токов остается синфазным и близко к треугольному, что соответствует весьма низкому уровню первого бокового лепестка (-26,4 дБ). Это существенно ниже, чем в главных плоскостях, наименее благоприятных с точки зрения бокового излучения. Если сравнить ширину ДН в главных и диагональной плоскостях квадратной АР, то они оказываются почти равными, так как спадание амплитуды к краям эквивалентной АР компенсируется увеличением ее длины по сравнению с размером стороны квадрата, определяющим ширину ДН в главных плоскостях.
. Длина эквивалентной решетки в рассматриваемом случае равна диагонали квадрата, а распределение токов остается синфазным и близко к треугольному, что соответствует весьма низкому уровню первого бокового лепестка (-26,4 дБ). Это существенно ниже, чем в главных плоскостях, наименее благоприятных с точки зрения бокового излучения. Если сравнить ширину ДН в главных и диагональной плоскостях квадратной АР, то они оказываются почти равными, так как спадание амплитуды к краям эквивалентной АР компенсируется увеличением ее длины по сравнению с размером стороны квадрата, определяющим ширину ДН в главных плоскостях.
При произвольном значении угла 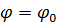 эквивалентная АР получается неэквидистантной. Для такой решетки ДН можно рассчитать как сумму ДН нескольких эквидистантных АР. Отметим, что при использовании реальных излучающих элементов множитель системы, соответствующий эквивалентной решетке, необходимо умножить на функцию, описывающую ДН одного элемента в плоскости
эквивалентная АР получается неэквидистантной. Для такой решетки ДН можно рассчитать как сумму ДН нескольких эквидистантных АР. Отметим, что при использовании реальных излучающих элементов множитель системы, соответствующий эквивалентной решетке, необходимо умножить на функцию, описывающую ДН одного элемента в плоскости 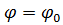 . Соответственно поляризационная характеристика поля излучения определяется поляризационными свойствами излучающего элемента в этой плоскости.
. Соответственно поляризационная характеристика поля излучения определяется поляризационными свойствами излучающего элемента в этой плоскости.
При несинфазном возбуждении элементов плоской АР для нахождения токов в элементах эквивалентной АР необходимо складывать токи соответствующих элементов плоской решетки с учетом фазы, т.е. складывать комплексные значения токов. Обратим внимание, что при отклоненном главном максимуме обычно рассматриваются сечения пространственной ДН в двух плоскостях: проходящей через ось z и направление 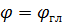 (условно вертикальная плоскость) и перпендикулярной ей, проходящей через направление максимума излучения. На основании метода эквивалентной линейной решетки можно утверждать, что для изотропных элементов по мере отклонения максимума излучения от нормали изменяется (расширяется) форма ДН только в вертикальной плоскости; во взаимно перпендикулярной ей плоскости форма ДН при отклонении не меняется.
(условно вертикальная плоскость) и перпендикулярной ей, проходящей через направление максимума излучения. На основании метода эквивалентной линейной решетки можно утверждать, что для изотропных элементов по мере отклонения максимума излучения от нормали изменяется (расширяется) форма ДН только в вертикальной плоскости; во взаимно перпендикулярной ей плоскости форма ДН при отклонении не меняется.
Отметим, что главные плоскости наиболее опасны с точки зрения возникновения вторичных максимумов, поскольку шаг эквивалентных решеток максимален именно в этих главных плоскостях. При размеще нии излучателей в узлах прямоугольной сетки он составляет dx и dy (см. рис. 14), во всех остальных сечениях шаг эквивалентной решетки меньше. Поэтому, если удовлетворяется условие
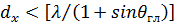 ,
, 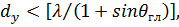 (54)
(54)
где 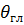 - угол отклонения максимума ДН в соответствующей плоскости относительно нормали к плоскости АР, то вторичные главные максимумы отсутствуют при отклонении ДН в любой плоскости.
- угол отклонения максимума ДН в соответствующей плоскости относительно нормали к плоскости АР, то вторичные главные максимумы отсутствуют при отклонении ДН в любой плоскости.
Для гексагональной сетки максимальный шаг эквивалентной решетки имеет место в сечении 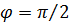 и составляет
и составляет 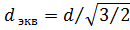 . Следовательно, при гексагональной сетке для устранения вторичных главных максимумов необходимо шаг d выбирать из условия
. Следовательно, при гексагональной сетке для устранения вторичных главных максимумов необходимо шаг d выбирать из условия
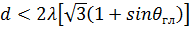 . (55)
. (55)
Указанное обстоятельство является преимуществом гексагональной сетки по сравнению с прямоугольной с точки зрения возможностей размещение излучающих элементов, поскольку условие (55) менее жесткое, чем (54).
Дата: 2018-11-18, просмотров: 600.