Знание входного сопротивления излучающего элемента в АР необходимо при проектировании системы питания, обеспечивающей требуемое АФР. Входное сопротивление каждого излучающего элемента ( 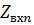) определяется не только его собственной конструкцией, но и взаимным влиянием соседних элементов, которое, в свою очередь, зависит от АФР возбуждающих токов и положения элемента в АР.

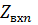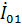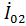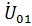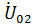Методика расчета на примере простейшей АР, состоящей из двух одинаковых излучателей, например, в виде СЭВ. Поскольку рассматриваемая система линейна, для токов и напряжений на входах каждого излучателя ( ,  и , соответственно) можно записать систему линейных уравнений типа уравнений Кирхгофа:

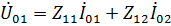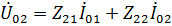, .                      (32)

Коэффициенты 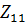, Z₂₂ носят название собственных сопротивлений, a Z₁₂, Z₂₁ - взаимных сопротивлений и имеют следующий смысл. Пусть второй вибратор разомкнут в точках входа, т.е. 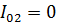. Тогда из первого уравнения (32) имеем 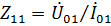. При разомкнутом первом вибраторе 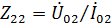. Таким образом, каждое из собственных сопротивлений равно входному сопротивлению соответствующего вибратора в режиме, когда другой вибратор разомкнут. В первом приближении обычно считают, что влияние разомкнутых вибраторов невелико (это справедливо, если длина плеч вибратора отлична от резонансной длины), и отождествляют собственное сопротивление с входным сопротивлением каждого вибратора в свободном пространстве.

В рабочем режиме, когда оба вибратора возбуждаются соответствующими напряжениями, из (32), поделив первое уравнение на 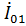, а второе на 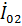, получим значения входных сопротивлений вибраторов в составе решетки:

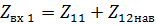,                          (33)

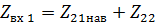,                         (34)

где добавочные сопротивления, входящие в состав входных сопротивлений, носят название наведенных сопротивлений, причем

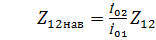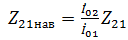, .                (35)

Как видно из (35), при равных токах, т.е. 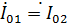, взаимные сопротивления равны наведенным. Отметим, что с помощью принципа взаимности можно показать, что Z ₁₂ = Z ₂₁, причем это равенство сохраняется при разных длинах вибраторов и произвольном взаимном расположении в пространстве. Для наведенных сопротивлений подобное равенство, как следует из (35), несправедливо, однако наведенные сопротивления могут быть найдены через взаимные, если известны токи на входах излучателей.

Для нахождения взаимного сопротивления вибраторов может быть использован метод наведенных ЭДС. Рассмотрим ситуацию, когда токи на входах вибраторов равны, т.е. 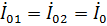, причем считаем, что распределение тока в вибраторе, работающем в составе АР, остается таким же, как в свободном пространстве. При этом (33) приобретает вид

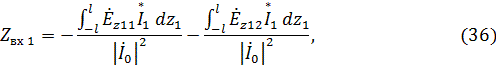
где .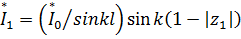

Сравнивая (36) с (33) при условии 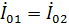, видим, что первое слагаемое в (36) может быть использовано для расчета собственного сопротивления Z ₁₁ , а второе - для расчета взаимного сопротивления Z ₁₂ = Z ₂₁. Расчет входных сопротивлений излучателей других типов встречает значительные сложности, поэтому часто используют экспериментальные данные.

Для решетки из N излучателей входное сопротивление каждого из излучателей рассчитывается по формуле, аналогичной (33) и (34):

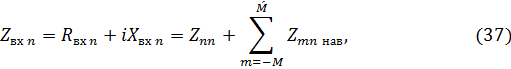
где Z_nn - собственное входное сопротивление n-го излучателя, Z_mn - наведенное сопротивление, отнесенное к току на входе n-го излучателя. Штрих при M знака суммы в (37) означает исключение члена с m=n. При этом в качестве 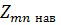обычно используются значения наведенных сопротивлений, обусловленные взаимодействием излучателей только с номерами m и n, без учета всех остальных элементов.