Выше предполагалось, что токи, возбуждающие элементы АР, синфазны либо распределение фазы имеет линейный характер. Именно такие фазовые распределения обычно используются на практике. Однако из-за неточностей изготовления решетки или из-за других факторов фазовое распределение может оказаться отличным от требуемого. Это отличие (фазовые ошибки) может носить систематический или случайный характер. Ограничимся случаем, когда фазовые ошибки пропорциональны первой, второй или третьей степени номера излучателя в решетке:

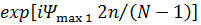(линейные ошибки),

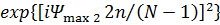 (квадратичные ошибки),

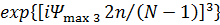 (кубические ошибки).

Здесь 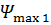, , 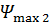 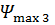- максимальные величины фазовых ошибок на краю решетки по сравнению с центральным элементом. При линейном исходном распределении фазы и линейных фазовых ошибках результирующее фазовое распределение примет вид

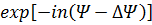,                          (31)

где 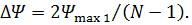Из (31) видно, что наличие фазовых ошибок не меняет линейного характера фазового распределения, а лишь изменяет результирующий сдвиг фаз между токами в соседних излучателях. При этом остаются справедливыми все формулы, полученные ранее для линейного фазового распределения, если в них вместо Ψ подставить ( 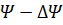). В частности, новое направление максимума излучения 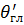, определяемое из соотношения 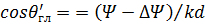, сместится на некоторый угол 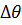, зависящий от знака фазовой ошибки. Величина  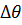не зависит от вида амплитудного распределения.

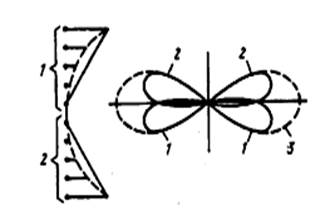
При квадратичных и кубических фазовых ошибках аналитические формулы для ДН становятся весьма громоздкими и здесь не приводятся. Элементарная трактовка происходящих при этом процессов может быть дана следующим образом. Пусть исходные токи являются синфазными 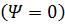. В первом приближении заменим квадратичное распределение фазы двумя линейными (рис. 9, а). Тогда каждую половину антенны можно рассматривать как решетку с линейным фазовым распределением, ДН которой отклоняется в сторону запаздывания фазы. С ростом  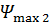суммарная ДН будет соответственно расширяться, причем независимо от знака 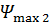. При больших  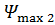появляется провал в середине основного лепестка. Точный анализ показывает, что помимо расширения основного лепестка ДН при квадратичных фазовых ошибках происходят увеличение УБЛ и исчезновение («заплывание») нулей ДН.

а)                                   б)

Рисунок 9. Замена распределения фазовых ошибок:

а) квадратичного распределения фазы двумя линейными,

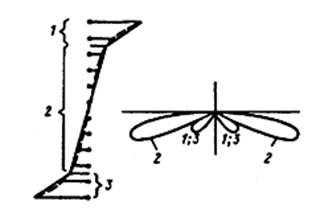
б) кубического распределения фазы ломаной линией

Кубические фазовые искажения в первом приближении можно аппроксимировать ломаной линией, каждый из отрезков которой соответствует линейному распределению фазы (рис. 9, б).

На рис. 9, б изображены также ДН каждой из частей решетки с линейным фазовым распределением (с учетом размеров каждой из частей). Суммарная ДН поворачивается, при этом увеличивается боковое излучение со стороны, в которую поворачивается максимум излучения. Степень искажений ДН, вызываемых фазовыми ошибками, снижается при амплитудном распределении, спадающем к краям решетки.

При произвольном законе амплитудно-фазового распределения (АФР) получение аналитических выражений, описывающих ДН, становится весьма сложной задачей. В этом случае для расчета ДН оказывается более целесообразным непосредственное суммирование полей от каждого элемента с применением ЭВМ.