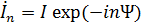,                                       (1)

т.е. токи во всех элементах равны по амплитуде, а фаза тока в каждом из элементов отстает от фазы в предыдущем на величину Ψ (линейный, или прогрессивный, закон изменения фазы (см рис. 2).

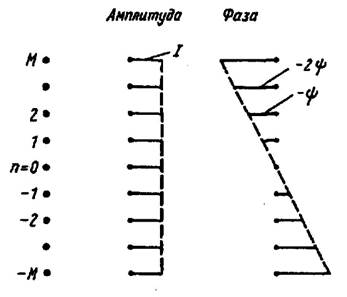
Рисунок 2. Распределение токов и фаз в линейной АР

Подобное распределение тока широко используется на практике. Заметим, что вопрос практической реализации требуемого распределения токов достаточно сложен, в частности, из-за эффекта взаимной связи, неодинаковой для центрального и крайних элементов. При настоящем анализе полагается, что токи в элементах решетки известны с учетом эффекта взаимной связи и ДН одного элемента в решетке остается такой же, как в случае уединенного излучателя.

В качестве элементов для простоты рассмотрим ненаправленные излучатели, поэтому при расчете ДН достаточно ограничиться анализом множителя системы.

Используя общие соотношения находим, что разность хода для n-го элемента по сравнению с центральным, расположенным в начале координат, 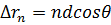, а множитель системы

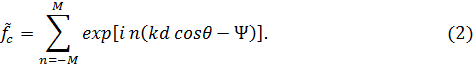
Выражение под знаком суммы в (2) представляет собой геометрическую прогрессию из N членов, знаменатель которой 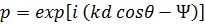, а первый член прогрессии, соответствующий n = -M, определяется как 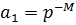. Используя формулу для суммы геометрической прогрессии, получаем

.

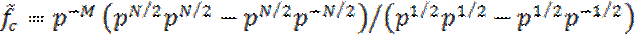Проведя преобразования получаем

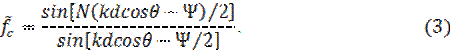
Выражение (3) получилось чисто вещественным. Это значит, что фазовая диаграмма направленности АР не зависит от угловых координат и лишь меняется скачком на 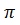при переходе через нуль выражения (3). Таким образом, линейная АР с распределением токов (1) независимо от величины Ψ излучает волну со сферическим фронтом и ее фазовый центр совпадает с серединой АР.

Выражение для нормированной амплитудной ДН (нормированный амплитудный множитель системы) имеет вид

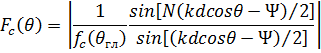
где 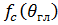 - значение функции  в направлении главного максимума 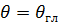. Знак модуля в дальнейшем для упрощения записи будем опускать. Величина 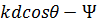в аргументе числителя и знаменателя последнего выражения характеризует сдвиг фаз между полями двух соседних элементов в дальней зоне. В зависимости от фазового сдвига изменяется положение максимума излучения. Соответственно различают режимы нормального, наклонного и осевого излучений.

Режим нормального излучения (Ψ = 0). При Ψ = 0 элементы решетки возбуждаются синфазно. Максимум излучения ориентирован по нормали ( ) к оси решетки, так как в этом направлении разность хода равна нулю и поля складываются синфазно. Это - режим нормального излучения. Диаграмма направленности описывается формулой

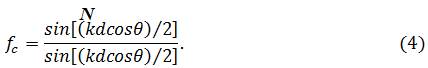
В направлении 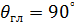 выражение (4) представляет собой неопределенность вида 0/0, при раскрытии которой по правилу Лопиталя получаем 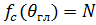. Соответственно нормированная ДН имеет вид

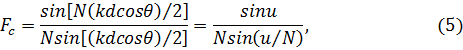
где .

Элементарное рассмотрение основных свойств линейной АР можно осуществить графически, не прибегая к анализу выражения (5). Каждое слагаемое в (2), пропорциональное полю излучения соответствую­щего элемента, будем изображать как вектор на фазовой (комплекс­ной) плоскости. На рис. 3 последовательно представлены векторные диаграммы для нескольких точек наблюдения. Еще раз подчеркнем, что рассматриваемые векторные диаграммы отражают фазовые соот­ношения между полями отдельных элементов и никак не связаны с расположением векторов в пространстве.

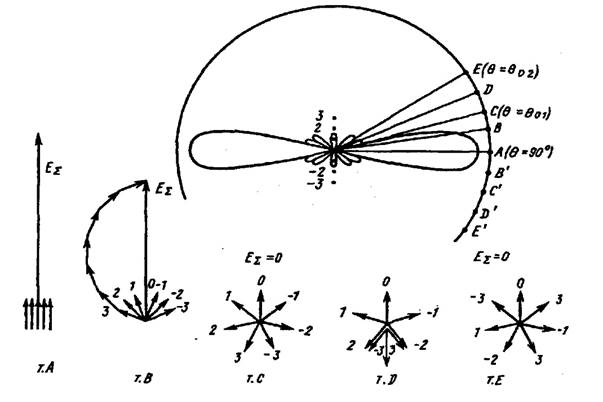
Рисунок 3. Векторные диаграммы для точек наблюдения A,B,C,D,E.

В точке А ( 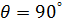, разность хода 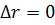) все векторы синфазны между собой, в результате суммарное поле имеет максимальное значе­ние. Таким образом, в направлении нормали к оси АР формируется максимум ДН.

В точке В синфазность сложения уже нарушается, при­чем векторы, соответствующие элементам с положительными индек­сами, опережают, а с отрицательными - запаздывают по отношению к вектору с индексом 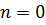 на величину 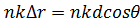. Для суммирова­ния векторов в точке В можно совместить начало каждого вектора с концом предыдущего и полученную ломаную замкнуть результирую­щим вектором (см. рис. 3), который будет меньшим, чем в точке А. При дальнейшем уменьшении угла  «веер» векторов раскрывается все сильнее, соответственно результирующий вектор становится все меньше, а в точке  С, угловое положение которой обозначим 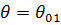, результирующий обратится в нуль. Как видно, фазовый сдвиг между отдельными векторами, равный 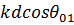; составляет в этой точ­ке 2 π / N . Отсюда

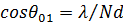.                             (6)

Заметим, что условие (6) может быть выполнено, только если 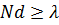. В противном случае в ДН отсутствуют направления с нулевым излучением.

Чем больше произведение Nd (чем длиннее решетка), тем уже основной лепесток ДН. При 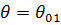 начинается область формиро­вания боковых лепестков. Максимум первого бокового лепестка полу­чается в точке D. Интересно отметить, что в области бокового излуче­ния векторы, соответствующие средним элементам, компенсируют друг друга (см. рис. 3) и суммарный вектор определяется только вкладом элементов, расположенных вблизи краев АР. Поэтому интенсивность боковых лепестков в принципе можно уменьшить, выбирая закон рас­пределения токов, спадающий к краям решетки.

В точке Е суммарный вектор опять обращается в нуль. При дальнейшем уменьшении угла 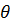 продолжается процесс формирования даль­них боковых лепестков. Однако при сравнительно большом d возможен случай, когда фазовый сдвиг между соседними векторами дости­гает величины 2 , т.е. все векторы опять оказываются расположенны­ми параллельно друг другу и их сумма дает дополнительный главный максимум. Это может иметь место при угле 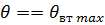 определяемом соотношением

.                                   (7)

Из (7) видно, что для исключения дополнительных главных максимумов в ДН синфазной решетки из изотропных элементов необ­ходимо выбирать

d < λ .                                                (8)

В точках В', С', D ', Е' векторные диаграммы имеют аналогич­ный вид, изменяется только знак фазового сдвига между полями со­седних элементов. Для построения ДН необходимо в радиальных направлениях, соответствующих рассмотренным точкам, отложить отрез­ки, пропорциональные результирующим векторам в каждой точке. Характерный вид подобной диаграммы (в плоскости, проходящей через ось решетки) приведен на рис. 3. При построении ДН учтена сим­метрия системы относительно оси решетки и плоскости, перпендику­лярной оси. Соответствующая пространственная ДН получается пу­тем вращения кривой, изображенной на рис. 3, вокруг оси решетки.

Перейдем к более детальному анализу ДН, описываемой выраже­нием (5). Направления, в которых излучение отсутствует, определяется из условия 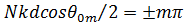, где т = 1,2,..., причем знак плюс соответствует углам 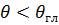, а знак минус - углам 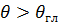. Соответственно находим

.                              (8)

При m=1 выражение (8) совпадает с полученным ранее (6). Если Nd >>λ (реально при 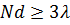), то из (8), используя формулу  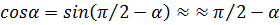 для углов 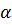, близких к 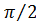, имеем 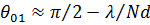.В силу симметрии диаграммы относительно нормали к оси решетки ширина основного лепестка ДН по уровню нулевого излучения определится по формуле

Направления максимумов боковых лепестков приближенно можно определить из условия максимума числителя (5), так как знаменатель этого выражения, особенно при большом Nd, меняется значительно медленнее числителя. Отсюда, приравнивая аргумент числителя , имеем

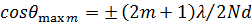.                 (10)

Подставляя значение 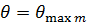 из (10) в (5), получаем уровень бокового лепестка (УБЛ):

Величина максимальна для , с ростом m интенсивность боковых лепестков сначала убывает, затем возрастает. Минимальное значение 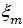 имеет при аргументе синуса в (11), равном 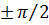. Угловое положение этих лепестков можно определить, приравняв аргумент синуса в знаменателе (5) к 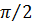, откуда получим 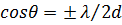.Ясно, что для исключения возрастания УБЛ необходимо выполнение условия

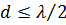.                                           (12)

Условие (12) предъявляет более жесткие требования к шагу решетки, чем требование (8), при котором отсутствуют дополнительные главные максимумы.

При большом значении 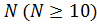 для первых боковых лепестков можно получить приближенную формулу

.                                (13)

Из (13) имеем, что при m =1 (первый боковой лепесток )уровень 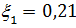 (или 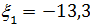 дБ) и не зависит от N.

На рис. 4, а приведена серия расчетных ДН, демонстрирующих зависимость ширины основного лепестка при различных N, на постоянном шаге решетки 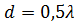. Серия ДН, приведенных на рис. 4, б для различных сочетаний N и d (но таких, что 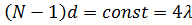, демонстрирует практическую неизменность основного лепестка и возникновение вторичных главных максимумов при .

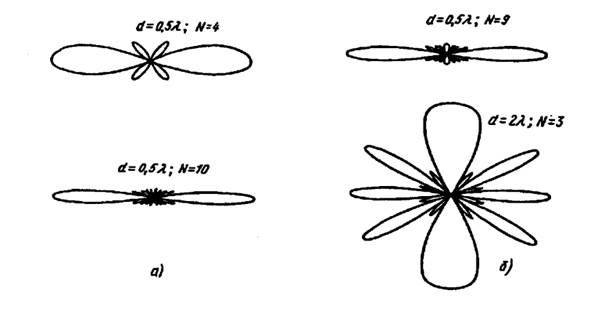
Рисунок 4. Расчетные ДН, демонстрирующие зависимость ширины основного лепестка при различных N

Режим наклонного излучения ( ).В этом режиме максимум излучения отклоняется от нормали к оси решетки, причем на такой угол, при котором разность фаз за счет разности хода для отдельных элементов компенсируется сдвигом фаз из-за не синфазности возбуждения. Рассмотрим, например, два соседних элемента с n = 0 и n = 1 (см. рис. 1). Разность фаз за счет разности хода для поля элемента с n = 1 по отношению к полю центрального элемента составляет 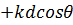, а за счет возбуждения фаза его поля отстает на величину (-Ψ). Компенсация наступает, когда 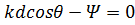, откуда

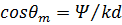.                                (14)

Из (14) видно, что при возрастании Ψ от нуля до kd направление максимума излучения отклоняется от нормали и приближается к оси решетки, т.е. отклоняется в ту же сторону, в которую происходит отставание фазы возбуждения элементов решетки (рис. 5). Эффект перемещения направления максимального излучения при изменении фазового сдвига Ψ находит широкое практическое применение в сканирующих АР.

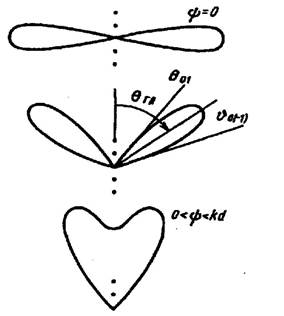
Рисунок 5. Отставание фазы возбуждения элементов решетки

Выражение для ДН в плоскости, проходящей через ось решетки, имеет вид как и для , причем , как и в случае синфазного возбуждения. Направления нулей излучения определяются из условия равенства нулю числителя (выражения для ), т.е. 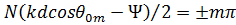, откуда

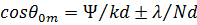.                           (15)

Ближайшим к главному максимуму направлениям нулевого излучения соответствуют углы 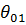 и 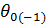 (см. рис. 6), причем

,

.

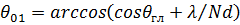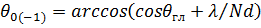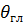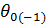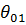В отличие от режима нормального излучения нули расположены несимметрично относительно . Ширина ДН по уровню нулевого излучения может быть определена как разность углов  и ,т.е.

.

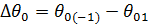При малых отклонениях максимума ДН от нормали и 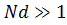 степень несимметрии невелика и величина  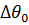может быть рассчитана по приближенной формуле

.                      (16)

Из (16) видно, что по мере увеличения отклонения ДН от нормали основной лепесток расширяется в  раз по сравнению со случаем синфазного возбуждения.