Задано множество альтернатив A == {а1, а2, ..., а m } и множество соответствующих исходов S = [ s 1 , s 2 , ..., sm ,}. Каждый исход sj характеризуется альтернативой а i и вектором лингвистических оценок на множестве критериев К = [К1, К2, .... К n }. Множество лингвистических векторных оценок исходов К = { K ( s 1 ), K ( s 2 ), ..., K ( sm )} можно упорядочить, введя функцию принадлежности нечеткого отношения порядка m ³: К ´ К ® [0,1]. Для i-го критерия обозначим mi ³ ( Ki ( sj ), Ki(sk)) через mi³ (sj , sk) Значение этой функции можно вычислить по фоомуле
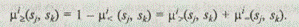
Степень истинности m < (sj , sk ) нечеткого высказывания sj < sk можно определить как вероятность того, что точное значение s j будет меньше точного значения sk . Предполагая, что исходы являются независимыми случайными величинами, отношение m < (sj , sk ) можно представить в виде:
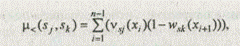
где vs ( x ) — вероятность того, что в качестве точного значения нечеткого числа s используется величина х;
ws ( x ) — вероятность того, что в качестве точного значения s используется величина у < х:
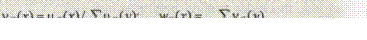
Векторные оценки могут быть упорядочены на основе функции принадлежности
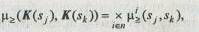
где х — обозначает символ обобщенной операции.
Так как между множеством альтернатив и исходив существует взаимно однозначное соответствие, функцию принадлежности нечеткого отношения предпочтения на множестве альтернатив можно представить в виде:
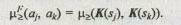
Решение задачи с использованием данного метода включает следующие основные шаги:
• вычисление функций принадлежности m< с использованием соотношений (4.2);
• построение нечеткого отношения порядка m³;
• минимизация отношения m³;
• определение отношений предпочтения на множестве альтернатив и выявление лучшей альтернативы. Для этого вычисляется отношение предпочтения между альтернативой aj и всеми остальными альтернативами, функция принадлежности которого имеет вид:
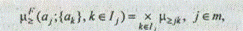
где Ij — множество индексов альтернатив, с которыми может сравниваться j-я альтернатива.
Решение задачи ранжирования можно описать соотношениями:
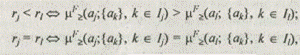
где rj — ранг альтернативы.
Наиболее предпочтительная альтернатива имеет самый низкий ранг.
Методика решения прикладных задач на ЭВМ
Многокритериальный выбор методом максимннной свертки в сфере банковского кредитования
Банковское кредитование
С развитием рыночных отношений процесс кредитования банками предприятий сопряжен с многочисленными факторами риска, способными повлечь за собой непогашение ссуды в установленный срок. При анализе кредитоспособности заемщика определяется возможность своевременного и полного погашения задолженности по ссуде; степень риска, которую банк готов взять на себя; размер кредита, который может быть предоставлен в конкретной ситуации; условия предоставления кредита.
В современных условиях анализ кредитоспособности связан не только с оценкой платежеспособности клиента на определенную дату, но и с выявлением наиболее предпочтительных заемщиков, прогнозированием их финансовой устойчивости в перспективе, учетом возможных рисков по кредитным операциям. Проведение такого всестороннего анализа позволяет банку более эффективно управлять кредитными ресурсами и получать прибыль.
Применяемые банками методы в области кредитования основаны на данных бухгалтерских отчетов, поэтому они позволяют лишь оценить кредитоспособность ссудозаемщика, не обеспечивая выбора наиболее оптимального заемщика в целях минимизации факторов риска для банка и наиболее эффективного планирования своей деятельности в будущем.
Рассмотрим применение метода принятия решений, основанного на теории нечетких множеств в области кредитования, позволяющего повысить обоснованность принимаемых решений и обеспечить выбор наиболее рационального варианта из множества допустимых.
К региональному отделению сберегательного банка России обратились четыре предприятия с просьбой о предоставлении им кредита. Поскольку ресурсы банка ограничены, перед ним стоит задача выбрать одно предприятие, лучшее по комплексу критериев качества. В рассматриваемой задаче предприятия являются альтернативами, из которых предстоит сделать выбор лучшей. Альтернативы обозначим через а1, ..., a 4.
Для оценки кредитоспособности предприятий-заемщиков используем данные их бухгалтерской отчетности (табл. 4.1).
Таблица 4.1
Дата: 2018-11-18, просмотров: 365.