Рассмотрим метод многокритериального выбора альтернатив на основе композиционного правила агрегирования описаний альтернатив с информацией о предпочтениях лица, принимающего решение, которые заданы в виде нечетких суждений [2].

Сущность метода, на основе которого реализована компьютерная система, заключается в следующем. Пусть U — множество элементов, А — его нечеткое подмножество, степень принадлежности элементов к которому есть число из единичного интервала [0, 1]. Подмножества A_j являются значениями лингвистической переменной X.

Допустим, что множество решений характеризуется набором критериев х₁, х₂, ..., x_p , т.е. лингвистических переменных, заданных на базовых множествах и₁, и₂, .... u_p соответственно. Например, переменная х₁ "качество управления" может иметь значение НИЗКОЕ, а переменная х₂ "стоимость" — значение ХОРОШЕЕ и т. д. Набор из нескольких критериев с соответствующими значениями характеризует представления лица, принимающего решение, об удовлетворительности альтернативы. Переменная S "удовлетворительность" также является лингвистической. Ниже приведен пример высказывания :

d ₁ : "Если x ₁ = НИЗКОЕ и x ₂ = ХОРОШЕЕ, то S = ВЫСОКАЯ". В общем случае высказывание d ₁ имеет вид:

d ₁ : "Если x₁ = А₁, и x ₂ = А_{2 i} и ... х_р = А_{р i} то S = В _i ". (4.1)

Обозначим пересечение (x ₁ = А_{1 i} Ç x ₂ = А_{2 i} Ç... х_р = А_{р i} ) через х = А _i . Операции пересечения нечетких множеств соответствует нахождение минимума их функций принадлежности:

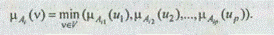
Здесь V = U ₁ ´U₂ ´...U_p; v = ( u ₁ , и₂ ..., u_p ); m _Aij (u_j) — значение принадлежности элемента и, нечеткому множеству А_ij.

Тогда высказывание (4.1) можно записать в виде:

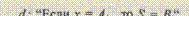
Для придания общности суждениям обозначим базовые множества U и V через W . Тогда А _i — нечеткое подмножество W , в то время как В _i — нечеткое подмножество единичного интервала I.

Для представления правил используется операция импликации, для которой предложены различные способы нечеткой реализации [4]. Нечеткая импликация Лукасевича имеет вид:

где Н — нечеткое подмножество на W ´ I, w Î W , i Î I.

Аналогичным образом высказывания d ₁ , d ₂ ,..., d_q преобразуются в множества Н₁, Н₂, ..., Н_q. Их пересечением является множество D :

D = H ₁ Ç H ₂ Ç ... Ç Н _q

и для каждого (w, i) Î W ´ I

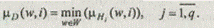
Удовлетворительность альтернативы, которая описывается нечетким подмножеством А из W, определяется на основе композиционного правила вывода:

G = А ° D,

 где G — нечеткое подмножество интервала I.

Тогда

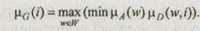
Сопоставление альтернатив происходит на основе точечных оценок. Для нечеткого множества С Ì I  определяем a-уровневое множество (a Î [0, 1]):

С_a= {i | m_c (i) ³ a Î I}.

Для каждого С_a можно вычислить среднее число элементов — М(С_a):

для множества из п элементов

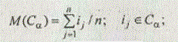
для С_a={a £ i £ b}

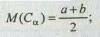
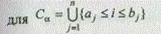
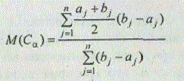
при 0 £ a ₁ £ b ₁ £ а₂ £ b ₂ £ ... £ а _n £ b_n £ 1.

Тогда точечное значение для множества С можно записать в виде:

где a_max — максимальное значение в множестве С.

При выборе альтернатив для каждой из них находится удовлетворительность и вычисляется соответствующая точечная оценка. Лучшей считается альтернатива с наибольшим ее значением.