| Критерий
| Оценка альтернативы
| |||
| а1 | a2 | a3 | a4 | |
| c1 | Средняя | Средняя | Низкая | Крайне низкая |
| c 2 | Высокая | Высокая | Средняя | Низкая |
| c 3 | Высокая | Высокая | Низкая | Крайне низкая |
| c 4 | Высокая | Низкая | Низкая | Средняя |
| c 5 | Низкая | Очень высокая | Высокая | Средняя |
| c 6 | Средняя | Средняя | Высокая | Высокая |
| c 7 | Высокая | Низкая | Низкая | Средняя |
| c 8 | Высокая | Средняя | Средняя | Средняя |
Аддитивная свертка представленной информации дала следующий результат:
mJ(j) = {1,0/a 1; 0,75/a 2; 0,68/a 3; 0,58/а4}.
что позволяет считать лучшей альтернативой стратегию по снижению цены а1.
Выбор предприятия для кредитования методом лингвистических векторных оценок
Решается задача выбора из трех альтернативных предприятий наиболее платежеспособного в целях предоставления кредита. Оценка альтернатив (а i) проводится по следующим критериям: с1 — общая ликвидность; с2 — обеспеченность собственными средствами; с3 — восстанавливаемость платежеспособности.
Сформируем векторный критерий С = {c 1, с2, c 3}. Оценки возможных исходов по критериям сi представлены нечеткими числами, заданными на базовом множестве Х = {1, 2, 3, ..., 10}. Множество лингвистических оценок TS = {ОН (очень низкий); Н (низкий); С (средний); В (высокий); OВ (очень высокий)}. Функции принадлежности термов имеют вид:
ОН = {1,0/1; 0,8/2; 0,2/3};
Н= {0,8/1; 0,9/2; 0,5/3; 0,2/4};
С = {0,3/3; 0,7/4; 1,0/5; 0,8/6; 0,2/7};
В = {0,2/7; 0,5/8; 0,9/9; 0,8/10};
ОВ = {0,2/8; 0,8/9; 1,0/10}.
Лингвистические векторные оценки альтернатив заданы матрицей:
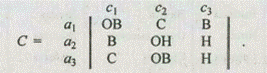
Суть данной методики заключается в вычислении оценки предпочтительности каждой из альтернатив относительно других. При этом, как и в случае максиминной свертки, сначала вычисляются наихудшие оценки для каждой альтернативы (m<), а после этого обратные им отношения предпочтительности (m³), среди которых выбирается максимальное.
Вычислим степень предпочтительности для альтернативы а1:
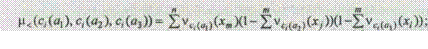
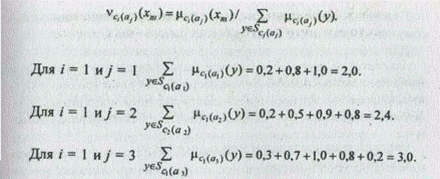
Аналогично находятся суммы по критериям c 2 и c 3. Функция принадлежности m<(a 1) вычисляется следующим образом:

Теперь вычислим нечеткое отношение m³( a 1 ):
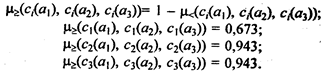
Степень предпочтительности альтернативы а1 равна минимальному из приведенных значений, т. е, m³( a 1 ) = 0,673. Для альтернативы а2 получены следующие оценки:

Степень предпочтительности m³( a 2 ) = 0,462.
Соответственно для а3.

Степень предпочтительности m³( a 3 ) = 0,709. Лучшей считается альтернатива, имеющая максимальную степень предпочтительности, т. е. a 3.
Дата: 2018-11-18, просмотров: 394.