Выбор метода зависит от измерительной задачи (точности результата, быстроты его получения и т.п.). На разработку метода измерений влияет выбор принципа измерения.
Принцип измерения заложен в совокупности тех физических явлений, которые лежат в основе данного измерения.
Существует два метода измерения (ГОСТ 16263-70): - метод непосредственной оценки и метод сравнения. Последний имеет несколько способов реализации: сравнение с методом замещения и совпадения, дифференциальный и нулевой.
Метод непосредственной оценки - определение измеряемой величины непосредственно по отсчетному устройству средства измерения прямого преобразования. Схема такого средства включает чувствительный элемент i, первичный измерительный преобразователь 2, нормирующий усилитель 3 и отсчетное устройство 4. Измеряемая входная величина Хвх, воздействуя на чувствительный элемент, инициирует сигнал измерительной информации Х1, который преобразуется первичным преобразователем, усиливается и инициируется как показание Хвых (наблюдаемое значение выходной величины).
 |
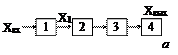1- 2-пер. измерительный преобраз.; 3-ЭУ; 4-ОУ.
 |
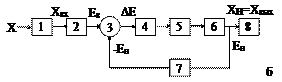1-ЧЭ; 2-Пер. преобраз; ЕВ-сигнал измерительной информации; 3-элемент сравнения; 4-индикатор рассогласования; 5-нормирующий усилитель; 6-измеряемая мера; 7-элемент компенсации; 8-ОУ
Рисунок 1.3 - Структурные схемы средств измерения прямого преобразования (а) и уравновешивания (б)
В методе прямого преобразования сравнение измеряемой величины с единицей измерения осуществляется косвенно путем предшествующей градуировки СИ по образцовому средству. При этом средство измерения потребляет энергию от объекта измерения и имеет однонаправленное преобразование сигнала измерительной информации. Метод непосредственной оценки имеет небольшую точность, но прост и экономичен.
Метод сравнения более точен и заключается в сравнении измеряемой величины с величиной, воспроизводимой мерой. Средства измерения при этом выполняются по схеме уравновешивания измеряемого сигнала. В структуре средств измерения при этом обязательно предусматривается обратная связь. Входной сигнал Хвх от чувствительного элемента 1 поступает на первичный измерительный преобразователь 2, с которого сигнал измерительной информации Ев поступает на элемент сравнения 3. На этот элемент также подается сигнал обратной связи ЕИ, имеющий обратный знак по отношению к Ев. Разность DЕ =Ев - Ен поступает на индикатор рассогласования 4, нормирующий усилитель 5, изменяемую меру 6, отсчетное устройство 8, Изменяемая мера позволяет получить образцовый сигнал Ен, который через элемент компенсации 7 подается на элемент сравнения. При равенстве Ен = Ев происходит уравновешивание (заканчивается изменение меры) и на отсчетном устройстве инициируется результат измерения Хвых.
Метод сравнения, в котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на элемент сравнения, называют методом противопоставления меры и измеряемой величины (аналитические весы). При сведении измерения к противопоставлению измеряемой величины и меры и измерению разности метод сравнения сводится к дифференциальному методу (измерительные мосты постоянного и переменного тока).
Если удается эту разность свести к нулевому значению путем изменения меры и сведения ее к измеряемой величине с большой точностью, то метод называют нулевым, а элемент сравнения выполняет роль нулевого индикатора (потенциометры постоянного тока).
Метод замещения также является разновидностью дифференциального, но при этом сравнение проводится в отличие от первого не одновременно, а разновременно (взвешивание на одной тарелке весов с поочередным помещением массы и гирь).
При измерении разности между мерой и измеряемой величиной путем совпадения шкал или периодических сигналов метод называют методом совпадения (измерение длины штангенциркулем).
Методы сравнения обеспечивает более высокую точность измерений, чем метод непосредственной оценки. Например, измеряемая величина определена методом непосредственной оценки с погрешностью 1 %. Допустим, что при использовании метода сравнения после уравновешивания разность между мерой и неизвестной величиной составляет 0,1 % и она будет оценена прибором с погрешностью 1%. Следовательно, погрешность измерения полного значения контролируемой величины составит всего 0,1 × 1:100 = 0,001 %.
Методика измерений - установленная совокупность операций измерения, выполнение которых обеспечивает получение результатов измерений в соответствии с выбранным методом измерений. Т.е. это технология выполнения измерений при помощи выбранного средства с целью наилучшей реализации метода измерения. Она регламентирует: выбор средства измерений, порядок выполнения операций, необходимость соблюдения числа и условий измерений, способов обработки их результатов.
Методика измерений после регламентации информативно-технической документации становится унифицированной.
Метрологические характеристики средств измерений
Для оценки пригодности СИ к измерениям с известной точностью вводят MX СИ с целью:
- обеспечения точности измерений;
- достижения взаимозаменяемости СИ, сравнения их между собой и выбора нужных СИ по точности и другим характеристикам;
- определения погрешностей измерительных СИ;
- оценки технического состояния СИ при поверке.
По ГОСТ 8.009—84 устанавливают перечень MX.
Каждая из видов MX по назначению представлена с учетом видов измерений и СИ в зависимости от изменений влияющих величин.
Неинформативным называется параметр входного сигнала СИ, не связанный функционально с измеряемым параметром. Например, частота переменного тока при измерении его амплитуды.
Наиболее распространены следующие MX СИ.
Диапазон измерений — область значений измеряемой величины, для которой нормированы допускаемые пределы погрешности СИ (для преобразователей — это диапазон преобразования).
Предел измерения — наибольшее или наименьшее значение диапазона измерения. Для мер — это номинальное значение воспроизводимой величины.
Например, у шкалы начальный участок (~20%) сжат, потому производить отсчеты на нем неудобно. Тогда предел измерения по шкале составляет 50 ед., а диапазон — 10...50 ед.
 |
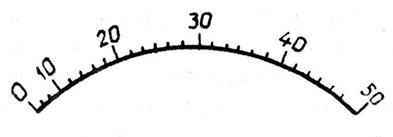Рис. Неравномерная шкала СИ
Цена деления шкалы — разность значений величин, соответствующих двум соседним отметкам шкалы. Приборы с равномерной шкалой имеют постоянную цену деления, а с неравномерной — переменную. В этом случае нормируется минимальная цена деления.
Чувствительность — отношение изменения сигнала Δу на выходе к вызвавшему это изменение измерению Δх сигнала на входе:
.
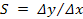Например, для стрелочного ИП — это отношение перемещения dl конца стрелки к вызвавшему его изменению dx измеряемой величины:
.
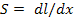Таким образом, для неравномерных шкал величина S = var , и степень неравномерности шкалы оценивают через коэффициент:
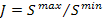
Для равномерных шкал:
S = Scp = const и S ср = l / xN ,
где xN — диапазон измерений.
Поскольку х и у могут быть выражены в различных единицах, то величина S имеет размерность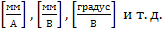 
Для чувствительности указывают чувствительность тока, напряжения и т. д.
Чувствительность нельзя отождествлять с порогом чувствительности— наименьшим значением измеряемой величины, вызывающим заметное изменение показаний прибора.
Величину, обратную чувствительности, называют постоянной прибора:
С = 1/ S .
Как правило, выходным сигналом СИ является отсчет (показание) в единицах величины. В этом случае постоянная прибора С равна цене деления. Поэтому для СИ с неравномерной шкалой чувствительность — величина переменная.
Вариация (гистерезис) — разность между показаниями СИ в данной точке диапазона измерения при возрастании и убывании измерений величины и неизменных внешних условиях:
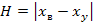
где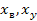 
— значения измерений образцовыми СИ при возрастании и убывании величины х.
Хотя вариация показаний СИ вызывается случайными факторами, сама она — не случайная величина.
Зависимость между выходным и входным сигналом СИ, полученную экспериментально, называют градуировочной характеристикой, которая может быть представлена аналитически, графически или в виде таблицы.
Градуировочная характеристика может изменяться под воздействием внешних и внутренних причин. Например, при быстром изменении тока подвижная часть СИ, вследствие инерции, не успевает "следить" за изменением тока. Градуировочная характеристика в этом случае должна выражаться дифференциальным уравнением.
Основная MX СИ — погрешность СИ — есть разность между показаниями СИ и истинными (действительными) значениями ФВ.
Все погрешности СИ в зависимости от внешних условий делятся на основные и дополнительные.
Основная погрешность — это погрешность СИ при нормальных условиях эксплуатации. Нормальные условия эксплуатации: температура 20±5°С, относительная влажность воздуха 65±15% при 20°С, напряжение в сети питания 220 В±10% с частотой 50 Гц±1%, атмосферное давление от 97,4 до 104 кПа, отсутствие электрических и магнитных полей (наводок).
В рабочих условиях, зачастую отличающихся от нормальных более широким диапазоном влияющих величин, при необходимости нормируется дополнительная погрешность СИ.
Существуют три способа нормирования основной погрешности СИ:
• нормирование пределов допускаемой абсолютной (±Δ) или приведенной (± γ ) погрешностей, постоянных во всем диапазоне измерения;
• нормирование пределов допускаемой абсолютной (±Δ) или относительной (±σ) погрешностей в функции измеряемой величины;
• нормирование постоянных пределов допускаемой основной погрешности, различных для всего диапазона измерений одного или нескольких участков.
Предел допускаемой погрешности - наибольшая погрешность, вызываемая изменением влияющей величины, при которой СИ по техническим требованиям может быть допущено к применению.
1) дополнительная погрешность имеет такой же вид, что и основная (абсолютная, относительная и приведенная);
2) дополнительные погрешности, вызванные различными влияющими факторами, должны нормироваться раздельно.
В общем виде суммарная абсолютная погрешность СИ при влияющих факторах
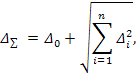
где Δ0 — основная погрешность СИ; Δi — дополнительная погрешность, вызванная изменением i-го влияющего фактора.
Иногда дополнительную погрешность нормируют в виде коэффициента, указывающего, "на сколько" или "во сколько" изменяется погрешность при отклонении номинального значения. Например, указание, что температурная погрешность вольтметра составляет ±1% на 10°С, означает, что при изменении среды на каждые 10°С добавляется дополнительная погрешность 1%.
Вследствие сложности разделения дополнительных и основных погрешностей поверку СИ выполняют только при нормальных условиях (т. е. дополнительные погрешности исключены).
Систематическая погрешность СИ — это составляющая общей погрешности, которая остается постоянной или закономерно изменяется при многократных измерениях одной и той же величины.
Случайные погрешности изменяются при повторных измерениях одной и той же величины случайным образом.
Статические погрешности возникают при измерении постоянных величин после завершения переходных процессов в элементах СИ.
Динамическая погрешность — разность между погрешностями СИ в динамическом режиме и его статической погрешностью.
В соответствии с ГОСТ 8.401—80 для пределов допускаемой основной (и дополнительной) погрешностей предусмотрены различные способы выражения в виде абсолютной, относительной и приведенной погрешности.
Абсолютная погрешность — разность между показанием х СИ и действительным значением хд измеряемой величины
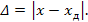
В качестве хд выступает либо номинальное значение (например, меры), либо значение величины, измеренной более точным (не менее чем на порядок, в 10 раз) СИ.
Абсолютная погрешность выражается в единицах измеряемой физической величины и может быть задана:
а) либо одним числом (линия 1 на рис. 3.4): Δ = ±а ;
б) либо в виде линейной зависимости (линии 2 и 3):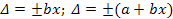 
Дата: 2019-12-10, просмотров: 263.
