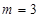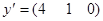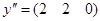На примере задачи выбора с тремя критериями ( ) рассмотрим следующие две оценки  и . Оценка  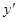по первому критерию «лучше» оценки  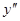(так как 4 > 2), а по второму критерию – «хуже» (1 < 2), тогда как по третьему критерию данные оценки равнозначны. Тем самым, при переходе от оценки  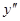к оценке  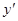ЛПР добавляет 2 единицы по первому критерию, но при этом теряет 1 единицу по второму критерию.

Предположим, что при сравнении этих двух оценок ЛПР выбрало первую - 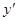. Спрашивается, каким образом можно объяснить сделанный ЛПР выбор? Почему ЛПР предпочло добавить две единицы по первому критерию, несмотря на потерю одной единицы по второму критерию?

Наиболее естественный ответ на поставленные вопросы состоит в следующем. Поскольку, ЛПР предпочло «прибавку» по первому критерию за счет «потери» по второму, это означает, что для данного ЛПР первый критерий является более важным, чем второй. Бόльшая степень важности для ЛПР одного критерия по сравнению с другим как раз и выражается в его готовности пожертвовать чем-то второстепенным (менее важным) во имя главного (более важного).

При этом для количественной оценки степени важности первого критерия по сравнению со вторым можно использовать отношение

,

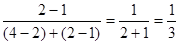выражающее долю «потери» по отношению к сумме «прибавки» и «потери». Чем больше эта доля, тем большую степень важности будет у одного критерия по сравнению с другим.

Приведенные выше рассуждения для трехмерных оценок ведут к следующим общим определениям, в которых для множества номеров критериев принято обозначение .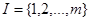

Определение 1. Говорят, что i -й критерий 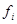 является более важным, чем j -й критерий  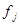( 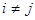) c положительными числовыми параметрам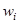и  и 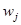, если для всех 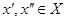, таких, что

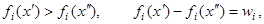
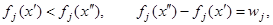
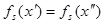для всех 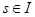, кроме  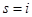и ,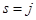

выполняется соотношение .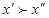

Заметим, что в данном определении присутствует отношение предпочтения 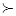, связанное с ЛПР. У каждого ЛПР свое собственное отношение предпочтения, а значит, если для одного ЛПР i-й критерий важнее j -го, то для другого ЛПР этого может и не быть. Иначе говоря, введенное понятие относительной важности критериев носит «субъективный» характер, что хорошо согласуется с интуитивными представлениями об этом понятии.

Определение 2. Пусть i-й критерий важнее j-го с положительными параметрами 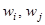 ( 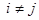). Число

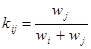
называется коэффициентом относительной важности критерия i по сравнению с критерием j.

Очевидно, 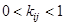, причем чем ближе этот коэффициент к 1, тем бόльшая степень важности y i -го критерия по сравнению с j-м; и наоборот, чем ближе  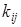к 0, тем меньше указанная степень важности. В «среднем» случае  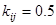ЛПР для получения «прибавки» по i -у критерию в размере  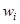единиц готово пожертвовать тем же количеством  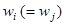по j-у критерию. Подобным образом можно дать интерпретацию любого числового значения коэффициента .

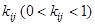Теперь, после того, как высказывание i -й критерий важнее j -го критерия с коэффициентом относительной важности 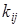 получило точный смысл, перейдем к обсуждению вопроса учета количественной информации об относительной важности критериев в процессе принятия решений.