Методы безусловной и условной оптимизации
Задача 1.
Найти
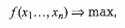(1)
где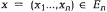 
Задача 1
сводится к решению системы уравнений:
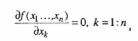(2)
и исследованию значения второго дифференциала:
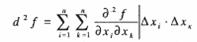(3)
в точках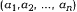 
решения уравнений (1).
Если квадратичная форма (2) отрицательно определена в точке, то она достигает в ней максимальное значение, а если положительно определена, то минимальное значение.
Пример:
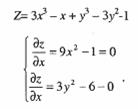(4)
Система уравнений имеет решения:
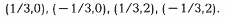
Точка (– 1/3,0) является точкой максимума, а точка (1/3,2) –точкой минимума.
Задача 2.
Найти
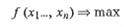(5)
при условиях:
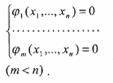(6)
Задача 2 решается методом множителей Лагранжа. Для этого находится решение системы (т + п) уравнений:
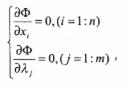(7)
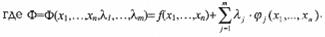(8)
Пример.
Найти стороны прямоугольника максимальной площади, вписанного в круг: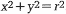 
. Площадь А прямоугольника можно записать в виде: А = 4ху, тогда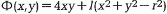 
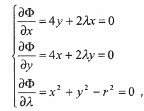
откуда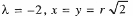 
Задача 3.
Найти:
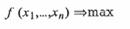(9)
при условиях:
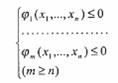(10)
Эта задача охватывает широкий круг задач, определяемых функциями f и j.
Если они линейны, то задача является задачей линейного программирования.
Задача 3а.
Найти
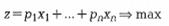(11)
при условиях
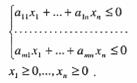(12)
Она решается симплекс-методом, который с помощью аппарата линейной алгебры производит целенаправленный перебор вершин многогранника, определяемого (12).
Симплекс-метод
(состоит из двух этапов):
Этап 1. Нахождение опорного решения х(0).
Опорное решение – одна из точек многогранника (12).
Этап 2. Нахождение оптимального решения.
Оптимальное решение находится последовательным перебором вершин многогранника (12), при котором значение целевой функции z на каждом шаге не уменьшается, то есть:
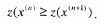
Частный случай задачи линейного программирования – так называемая транспортная задача.
Транспортная задача.
Пусть в пунктах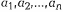 
находятся склады, в которых хранятся товары в количестве 
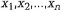соответственно. В пунктах 
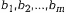находятся потребители, которым необходимо поставить эти товары в количествах 
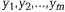соответственно. Обозначим cij стоимость перевозки единицы груза между пунктами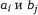 
Исследуем операцию перевозки потребителями товаров в количествах, достаточных, чтобы удовлетворить потребности потребителей. Обозначим через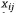 
количество товара, перевозимого из пункта аi в пункт bj.
Для того, чтобы удовлетворять запросы потребителя, необходимо, чтобы величины хij удовлетворяли условиям:
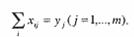(13)
В то же время со склада а; нельзя вывезти продуктов в большем количестве, чем там имеется. Это означает, что искомые величины должны удовлетворять системе неравенств:
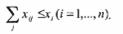(14)
Удовлетворять условиям (13), (15), то есть составить план перевозок, обеспечивающий запросы потребителей, можно бесчисленным числом способов. Для того, чтобы исследователь операций мог выбрать определенное решение, то есть назначить определенные хij, должно быть сформулировано некоторое правило отбора, определяемое с помощью критерия, который отражает наше субъективное представление о цели.
Проблема критерия решается независимо от исследования операции – критерий должен быть задан оперирующей стороной. В данной задаче одним из возможных критериев будет стоимость перевозки. Она определяется следующим образом:
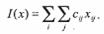(15)
Тогда задача о перевозках формулируется как задача линейного программирования: определить величины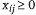 
, удовлетворяющие ограничениям (13), (14) и доставляющие функции (15) минимальное значение. Ограничение (14) – это условие баланса; условие (13) можно назвать целью операции, ибо смысл операции в том и состоит, чтобы обеспечить запросы потребителей.
Эти два условия составляют, по существу, модель операции. Реализация операции будет зависеть от критерия, при помощи которого будет обеспечено достижение цели операции. Критерий может фигурировать в различных ролях. Он может выступать и как способ формализации цели и как принцип выбора действий из числа допустимых, то есть удовлетворяющих ограничениям.
Одним из известных методов решения транспортной задачи является метод потенциалов.
На первом этапе решения задачи составляется первоначальный план перевозок, удовлетворяющий
ограничениям (13), (14). Если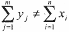 
(то есть суммарные потребности не совпадают с суммарными запасами продуктов на складах), то вводится в рассмотрение фиктивный пункт потребления 
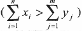или фиктивный склад 
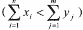со стоимостью перевозок, равными нулю. Для новой задачи суммарное количество товаров на складах совпадает с суммарной их потребностью. Затем каким-нибудь методом (например, наименьшего элемента или северо-западного угла) находится первоначальный план. На следующем шаге процедуры полученного плана строится система специальных характеристик – потенциалов. Необходимым и достаточным условием оптимального плана является его потенциальность. Процедура уточнения плана производится до тех пор, пока он не станет потенциальным (оптимальным).
Задача 3б.
В общем случае задача (9 – 10) называется задачей нелинейного программирования. Рассмотрим ее в более принятом виде:
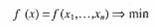(16)
при условиях
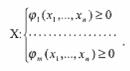(17)
Для решения этой задачи используются так называемые релаксационные методы. Процесс построения последовательности точек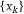 
называется релаксационным, если:
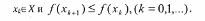
4.10 Методы спуска (общая схема).
Все методы спуска решения задачи безусловной оптимизации (16) различаются либо выбором направления спуска, либо способом движения вдоль направления спуска. Методы спуска состоят в следующей процедуре построения последовательности {xk}.
В качестве начального приближения выбирается произвольная точка x0. Последовательные приближения строятся по следующей схеме:
• точке xk выбирается направление спуска – sk;
• находят (к + 1) – е приближение по формуле:
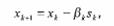(18)
где в качестве величины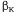 
выбирают любое число, удовлетворяющее неравенству
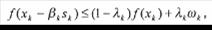(19)
где число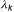 
– любое такое число, когда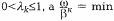 
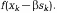
В большинстве методов спуска величина lк выбирается равной единице. Таким образом, для определения bк приходится решать задачу одномерной минимизации.
Метод градиентного спуска.
Поскольку антиградиент –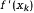 
указывает направление наискорейшего убывания функции f(x), то естественным является перемещение из точки хk по этому направлению. Метод спуска, в котором 
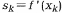называется методом градиентного спуска. Если 
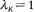, то релаксационный процесс называется методом скорейшего спуска.
Дата: 2019-12-10, просмотров: 200.
