Вернемся к задаче 36 ((16) – (17)):
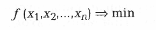
при условиях
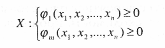
В оптимизационных задачах с ограничениями выбор направления спуска сопряжен с необходимостью постоянной проверки того, что новое значение хk+1 должно также, как и предыдущее xk удовлетворять системе ограничений X.
Метод условного градиента.
В этом методе идея выбора направления спуска состоит в следующем: в точке хк линеаризуют функцию f(x), строя линейную функцию 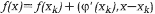 и затем, минимизируя f(x) на множестве х, находят точку yk. После этого полагают
и затем, минимизируя f(x) на множестве х, находят точку yk. После этого полагают 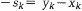 и далее вдоль этого направления осуществляют спуск
и далее вдоль этого направления осуществляют спуск 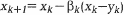 , так, чтобы
, так, чтобы 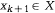
Таким образом, для отыскания направления – sk следует решить задачу минимизации линейной функции на множестве X. Если X в свою очередь задается линейными ограничениями, то она становится задачей линейного программирования.
Метод возможных направлений.
Идея метода: среди всех возможных направлений в точке хк выбирают то, вдоль которого функция f(x) убывает быстрее всего, и затем осуществляют спуск вдоль этого направления.
Направление – s в точке х Î X называется возможным, если существует такое число 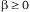 , что
, что 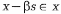 для всех
для всех 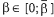 . Для нахождения возможного направления необходимо решить задачу линейного программирования, либо простейшую задачу квадратичного программирования:
. Для нахождения возможного направления необходимо решить задачу линейного программирования, либо простейшую задачу квадратичного программирования: 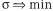
При условиях:
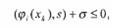 (24)
(24)
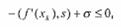 (25)
(25)
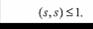 (26)
(26)
Пусть 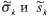 – решение этой задачи. Условие (24) гарантирует, что направление –
– решение этой задачи. Условие (24) гарантирует, что направление – 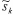 – возможное. Условие (25) обеспечивает максимальность величины (
– возможное. Условие (25) обеспечивает максимальность величины ( 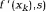 , то есть среди всех возможных направлений – s, направление –
, то есть среди всех возможных направлений – s, направление – 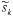 обеспечивает самое быстрое убывание функции f(x). Условие (26) избавляет от неограниченности решения задачи. Метод возможных направлений устойчив к возможным вычислительным ошибкам. Однако скорость его сходимости оценить в общем случае сложно и эта задача пока остается нерешенной.
обеспечивает самое быстрое убывание функции f(x). Условие (26) избавляет от неограниченности решения задачи. Метод возможных направлений устойчив к возможным вычислительным ошибкам. Однако скорость его сходимости оценить в общем случае сложно и эта задача пока остается нерешенной.
Метод случайного поиска.
Реализация изложенных выше методов минимизации в общем случае очень трудоемка, кроме простейших случаев, когда множество ограничений обладает простой геометрической структурой (например, является многомерным параллелепипедом). В общем случае весьма перспективным может быть метод случайного поиска, когда направление спуска выбирается случайным образом. При этом мы будем существенно проигрывать в скорости сходимости, однако простота выбора направления может компенсировать эти потери с точки зрения общих затрат труда на решение задачи минимизации.
Схема метода:
На n-мерной единичной сфере с центром в начале координат выбирается случайная точка rk, подчиняющаяся на этой сфере равномерному распределению, и затем направление спуска – sk из условий 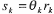 ,
,

В качестве начального приближения выбирается 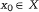 . По вычисленной на каждой итерации точке xk строится (k + 1)-я точка xk+1:
. По вычисленной на каждой итерации точке xk строится (k + 1)-я точка xk+1:
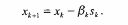
В качестве 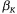 выбирается любое число из
выбирается любое число из 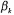 =
= 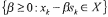 , удовлетворяющее неравенству:
, удовлетворяющее неравенству:
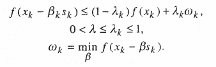
Доказана сходимость этого метода при весьма нежестких ограничениях на функцию f (выпуклость) и множество ограничений X (выпуклость и замкнутость).
Дата: 2019-12-10, просмотров: 337.