Результатом решения прямой динамической задачи обычно является СВР в виде импульсных сейсмотрасс, которые затем подвергаются свертке с импульсом, моделирующим сейсмический сигнал. Успех использования СВР для целей интерпретации во многом определяется правильным выбо­ром начального приближения этого импульса.

В связи с этим в практике моделирования применяется следующая методи­ка выбора сейсмического импульса. Основой этой методики является аналитическое выражение импульса Пузырева:

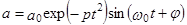,                                                                                    (3.1)

где a₀ – начальная амплитуда (обычно a₀ = 1); w₀ = 2p f₀ – преобла­дающая частота, Гц; р – затухание; j – начальная фаза.

Определение начального приближения параметров этого импульса (w₀, p, j) производится следующим образом. Начальная фаза j прини­мается равной p/2 (симметричный импульс) на основании того, что в процессе обработки реальных сейсмических записей в результате приме­нения всех видов фильтраций (деконволюция, полосовая фильтрация) стремятся на выходе получить элементарный сигнал симметричной формы (нуль-фазовый).

Преобладающая частота f₀ находится по спектру мощности реальных записей, для чего в заданном фрагменте временного разреза по всем трас­сам вычисляются нормированные автокорреляционные функции, которые затем осредняются, в результате чего получается одна функция 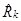. Для этой функции, предварительно сглаженной, вычисляется спектр мощности. Квадратный корень из этого спектра принимается за осредненный амплитудный спектр сейсми­ческого импульса. Этот спектр нормируется, и по нему находятся два параметра: преобладающая частота f₀ и ширина спектра Df на уровне 0,7.

Для определения параметра затухания р используется аналитическое выражение для нормированного амплитудного спектра импульса (3.1) в виде:

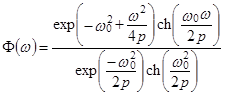.                                                                          (3.2).

Вначале по этой формуле при известном w₀ = 2p f₀ и p = 5000 вычисляет­ся амплитудный спектр теоретического импульса (3.1), по которому также на уровне 0,7 оценивается ширина спектра Df⁽¹⁾ (первая итера­ция). Это значение Df⁽¹⁾ сравнивается с определенным по спектру реальных сейсмозаписей значением Df, и если Df⁽¹⁾ > Df, то первоначальное р уменьшается, и наоборот. С новым значением р опять вычисляется по формуле (3.2) спектр F(w), по которому находится новое значение Df⁽²⁾ (вторая итерация) и т. д. Шаг изменения по р вначале принимается равным 1000, а после получения "вилки" он уменьшается до тех пор, пока не будет выполнено условие |Df⁽ⁱ⁾ – Df| £ 2 Гц, тогда значение р фиксируется.

Полученные оценки w₀ и p, а также принятое значение j = p/2 исполь­зуются для расчета по формуле (3.1) весовых коэффициентов фильтра для свертки с синтетическим временным разрезом в импульсном представ­лении.

Рассмотренная, методика предназначена для определения начального приближения пара­метров импульса, которое, как правило, является достаточно хорошим для параметров w₀ и p, но принимаемая априори величина j = p/2 может быть весьма приближенной, поскольку на реальном временном разрезе сигнал может отличаться от нуль-фазового. Поэтому в дальнейшем в про­цессе итеративной коррекции параметров модели все три параметра им­пульса также корректируются.

Раздел 3.4. Сопоставление синтетического и
реального временных разрезов

В соответствии с общими принципами анализа двумерных изображений сопоставляемые объекты должны быть разбиты на элементарные единицы, называемые сегментами. В нашем случае (при сравнении РВР и СВР) это понятие обозначает наименьшие элементы (DX, Dt), которые сохраняют физико-геологический смысл. Конкретно: сегменты, выделяе­мые на сопоставляемых временных разрезах, ограничиваются по оси t интервалом с одним или двумя опорными отражениями или таким интер­валом между опорными отражениями, который может представлять само­стоятельный интерес для моделирования, по оси Х – участком, который характеризуется примерно одинаковым характером записи и в определенной степени соответствует понятию сейсмофации, принятому в сейсмостратиграфии. Необходимо также отметить, что процедура сегментации, являясь неформальной в принципе, выпол­няется интерпретатором, а те соображения, которыми он руководствуется при выделении сегментов, создают для каждого из них свой контекст при сопоставлении реального и синтетического разрезов.

Наиболее естественной и наглядной являлась бы оценка, характеризую­щая в целом сходство соответствующих друг другу (т. е. имеющих один и тот же физико-геологический смысл) сегментов реального и синтетиче­ского разрезов. Однако для упрощения будем сопоставлять только участки трасс, входящих в указанные сегменты. Это позволяет свести двумерную (по Х и t) задачу оценки сходства к сово­купности одномерных (только по t) задач. По существу предполагается при этом, что волновое поле квазистационарно по X-координате.

Переходя непосредственно к численному оцениванию сходства трасс РВР и СВР, прежде всего, выделим две группы таких оценок:

1) инте­гральные оценки, характеризующие общий вид сравниваемых объектов;

2) дифференциальные, характеризующие отдельные их элементы.

При оценивании сходства по интегральным критериям основной операцией является интегрирование с использованием полной информации об объек­тах, а по дифференциальным критериям – дифференцирование, которое применяется как к объектам в целом, так и к их частям. Конкретные виды критериев сходства трасс СВР и РВР рассматриваются ниже.

Отметим лишь одно, важное в методическом аспекте обстоятельство. Достаточно высокий уровень глобальных оценок сходства, построенных по интегральным и дифференциальным критериям, играет роль соответственно необходимого и достаточного усло­вия достижения цели интерпретации. Это значит, что в процессе интерпре­тации при оценивании сходства с необходимостью нужно переходить от интегральных критериев к дифференциальным. Фактически это соответ­ствует наращиванию степени детальности рассмотрения сравниваемых раз­резов.

Так, при решении стратиграфических задач, вызывающих повышенный интерес в связи с проблемой прогнозирования геологического разреза, очевидно, нельзя заканчивать процесс интерпретации по достижению вы­сокой степени сходства по интегральным критериям, поскольку геологи­ческая сущность таких задач часто выражается в столь незначительных вариациях сейсмогеологической модели и соответствующего ей СВР, чув­ствительностью к которым обладают лишь дифференциальные критерии. Подобного рода чувствительность достигается усложнением процедуры оценивания сходства или построением этой процедуры на итеративно-диалоговых принципах, чем обеспечивается соответствие оцен­ки сходства визуальным и геолого-геофизическим представлениям интер­претатора.

Из рис. 7, а видно, что применение интегральных критериев требует осторожности, поскольку здесь при очевидном отсутствии визуального сходства значение интегральной оценки довольно высоко (0,84). Рис. 7, б и в демонстрируют слабую чувствительность интегрального критерия к малоамплитудным (локальным) особенностям записи: если учесть форму последнего полупериода записи, трассы на рис. 7, 6 визуально более похо­жи между собой, чем трассы на рис. 7, в. Однако значения сходства по НФВК противоречат этому суждению. Рис. 7, г, д и е иллюстрируют тот факт, что числовые значения интегральных и дифференциальных оценок могут отличаться весьма существенно. Кроме принципиальной разницы в подходах к оцениванию сходства, это объясняется еще и тем, что при вычислении дифференциальных оценок учитывается качественная инфор­мация от геофизика-интерпретатора. Так, выполнив стратиграфическую привязку отражений, он может выделить отражения, являющиеся целевы­ми в решаемой им геологической задаче, и задать их как наиболее важные при оценивании сходства.

Главной методической целью получения оценок сходства является выделение на каждом шаге итеративного процесса интерпретации тех трасс СВР и РВР, сходство между которыми ниже принятого на данном шаге порога. Наличие протяженных участков СВР, характеризующихся пониженными значениями оценок сходства, указывает на необходимость коррекции соответствующего фрагмента сейсмогеологической модели (иногда вплоть до перехода к другой гипотезе о строении геологического разреза).

Раздел 3.5. Целенаправленная коррекция параметров
тонкослоистых моделей

Как и ранее, будем ориентироваться на класс комбинированных моделей геологических сред, введенный в гл. 2. Напомним, что такие модели состоят из собственно моделируемого интервала, представленного совокупностью тонких слоев, и толстослоистой покрывающей части. В число корректируемых параметров включаются скорости, плотности и мощности тонких слоев, а также параметры импульса, моделирующего сейсмический сигнал.

Из методических соображений разделим процесс оптимизации целевой функции, связывающей оценки сходства с параметрами сейсмомоделирования, на два этапа:

1) предварительная коррекция, выполняемая в диалоговом режиме, когда в процессе коррекции предполагается постоянное и непосредствен­ное участие геофизика-интерпретатора;

2) уточнение параметров моделей в автоматическом режиме путем оптимизации некоторого функционала, описывающего сходство трасс реального и синтетического временных разрезов.

Предварительная коррекция

На этапе предварительной коррекции осуществляется сравнительно грубый подбор параметров модели в диало­говом режиме. Наличие данного этапа позволяет не вводить каких-либо ограничений на величину отклонения параметров модели нулевого при­ближения от искомого решения. Но вместе с тем если при первой оценке сходства (визуальной или по НФВК) синтетического и реального времен­ных разрезов обнаруживается явное их несходство, то ставится вопрос об изменении модели в целом или о переходе к другой гипотезе о геологи­ческом строении разреза.

Методической основой предварительной коррекции являются следующие положения:

1) при коррекции используются данные о сравнительной чувствитель­ности динамических характеристик записи к изменению параметров тонко­слоистой модели, полученные с помощью метода статистических испыта­ний;

2) в целях ограничения области поиска глобального экстремума из пер­вого этапа исключается и переносится на второй этап коррекция двух пара­метров исходного импульса (р, j) и в некоторых случаях коррекция толщин слоев;

3) для коррекции систематического отклонения толщин или скоростей в слоях, выражающегося в растяжении или сжатии трасс синтетического разреза, применяются формулы, которые учитывают значения первона­чальной скорости и толщины слоя;

4) на каждом шаге коррекции используются результаты сравнения СВР и РВР по НФВК, которые в конце предварительной коррекции могут дополняться сравнением по частным критериям (графики амплитуд и энергий, частотные спектры и др.) или с помощью дифференциальной оценки сходства.

Рассмотрим подробнее перечисленные положения.