Полный и точный учет амплитуд­ного фактора фокусировки сейсмической энергии возможен при сопостав­лении элементу отражающей границы пунктов взрыва-приема (ПВП), которые могут иметь нормальное отражение от этого элемента. Величина указан­ного элемента должна быть такой, чтобы часть среды, ограниченная норма­лями от его концов, удовлетворяла определению лучевой трубки. Всю со­вокупность траекторий нормальных лучей, необходимую для построения временного разреза, можно получить, рассмотрев все элементы всех отра­жающих границ модели среды.

Алгоритм нахождения траекторий нормальных лучей применяется в ходе просмотра с заданным шагом DX всех отражающих границ задан­ной модели. Если величина шага достаточно мала, ПВП, которые могут иметь нормальные отражения от рассматриваемого элементарного участка отражающей границы, располагаются между точками выхода нормалей, трассированных из его концевых точек. Для каждого полученного таким образом ПВП ведется поиск такого нормального луча, точка выхода кото­рого с заданной точностью совпадает с X-координатой этого ПВП. Итеративный алгоритм трассирования нормальных лучей из внутрен­них точек указанного элементарного участка позволяет завершить поиск, затратив минимальное количество трассированных лучей, что важно с точки зрения быстродействия программы.

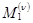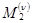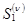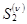Обозначим через  и  абсциссы точек, ограничивающих (со­ответственно слева и справа) рассматриваемый элемент отражающей гра­ницы на n-м шаге итерационного процесса, через  и  абсциссы точек выхода на поверхность нормалей к отражающей границе в точках с абсциссам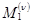и  и 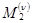 соответственно, а через XN – абсциссу ПВП (рис. 9, а).

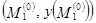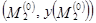Сначала из точек  и  отражающей границы восстанавливаются нормали, для двух полученных точек выхода с абс­циссам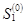и  и 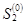 проверяется условие  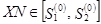и таким образом определяются количество и номера ПВП, находящихся между точками выхода нормалей. Именно здесь элементу отражающей границы ставится в соответствие ПВП, которые могут иметь нормальное отражение от него. Если данному условию не удовлетворяет ни один ПВП, делается следующий шаг по отражающей границе. Для каждого ПВП из интервала  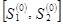проверяется условие

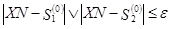,                                                                                        (4.1)

где e – заданная малая величина. Выполнение (4.1) означает конец итера­ционного процесса, а его результаты определяются траекторией, соответ­ствующей 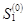, ес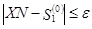ли , ил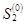и  при .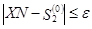

В случае, когда таким путем траектория не найдена, а элемент отражаю­щей границы не меньше заданной величины, из точки отражающей границы с абсциссой

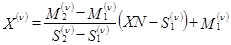
восстанавливается нормаль к отражающей границе. Если абсцисса 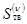 ее точки выхода достаточно близка к ПВП, т. е. 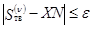, считается, что искомая траектория определена. В противном случае проверяется усло­вие принадлежности  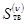интервалу 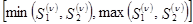. Если это условие выполнено, происходит переход к следующей итерации:

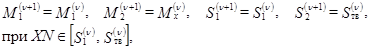
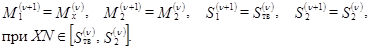
Невыполнение этого условия означает, что рассматриваемый элемент модели не является лучевой трубкой, и если он не слишком мал, то отрезок отражающей границы между точками с абсциссам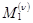и  и 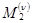 де­лится пополам, после чего процесс поиска начинается как бы снача­ла (n = 0).

По исчерпанию всех ПВП, найденных в интервале 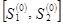, делается следующий шаг по отражающей границе.

Учет динамических факторов

Амплитуды отражений рассчитываются на основе следующих положений теории распространения волн:

1) непре­рывность напряжений и смещений для плоских волн, отражающихся от плоских границ;

2) сохранение энергии внутри лучевой трубки;

3) по­стоянный параметр поглощения Q, учитывающий минимально-фазовый механизм потерь при распространении за счет поглощения энергии.

Условия непрерывности на границе дают для коэффициента отражения простейшую формулу, строго справедливую в рассматриваемом случае нормального падения луча:

,

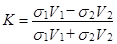где 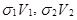 – акустические жесткости слоев, лежащих соответственно выше и ниже отражающей границы.

Для учета геометрического расхождения воспользуемся известной фор­мулой:

,

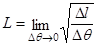где L – коэффициент геометрического расхождения; Dl – поперечный размер сечения лучевой трубки плоскостью паде­ния волны в точке наблюдения; Dq – интервал углов выхода, ограничи­вающий лучевую трубку. Обозначив R амплитудный фактор расхождения, с учетом соотношения R = L^-2

R= 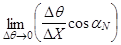,                                                                                               (4.2)

здесь Dq и DX – приращения угла засылки лучей и точек их выхода соот­ветственно; a _N – угол выхода нормального луча.

На основе формулы (4.2) построен итеративный алгоритм вычисления амплитудного фактора R, учитывающего геометрическое расхождение. Упрощенное описание его сводится к следующему.

Шаг 1. Засылка из данного пункта взрыва-приема пяти лучей с углами q _N-F, q _N‑F/2, q _N, q _N+F/2 и q _N+F и получение соответствующих точек выхода (F – малая величина порядка ~ 10^-4 – 10^-5, задаваемая в исходных данных).

Шаг 2. Формирование из пяти трассированных на шаге 1 лучей систе­мы из двух пар лучей так, чтобы каждая пара вмещала бы данный ПВП и чтобы одна из пар вмещала другую (см. рис. 9, б); вычисление двух значений амплитудного фактора R:

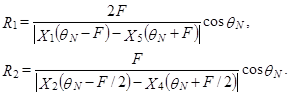
Шаг 3. Проверка предельного перехода

.

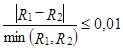Если "да", то R=R₂ и алгоритм заканчивается. Если "нет", проверяется условие |X₁‑X₅| < 50. При невыполнении этого условия расхождение считается вычисленным условно. В случае выполнения приращение увеличивается в 2 раза. Переход к шагу 1. При этом делается не более 16 попыток достигнуть сходимости в формуле (4.2) за счет увеличения F.

С учетом вышерассмотренных динамических факторов вычисляется импульсный временной разрез, в котором до свертки с заданным сейсми­ческим сигналом можно также произвести учет частотно-зависимого погло­щения сейсмической энергии.

Влияние фокусировки сейсмической энергии на амплитуду отраженных сигналов учитывается автоматически в ходе вычисления траекторий нор­мальных лучей. Явления фокусировки возникают при наличии локальных отрицательных перегибов в поведении границ (вогнутостей), когда нор­мальные лучи пересекаются (образуют каустики) в непосредственной бли­зости от линии наблюдения. Примером могут служить участки перехода от горизонтальной границы к крылу пологой структуры. В этом случае для одного и того же ПВП находятся два и более нормальных лучей с почти равными временами прихода отраженных сигналов которые автоматически суммируются.